If the time period (T)of vibration of a liquid drop depends on surface tension (S) , radius(r) of the drop , and density (ρ) of the liquid , then find the expression of T.
T=k√ρr3S
T=k ⎷ρ12r3S
T=k ⎷ρr3S12
None of these
The correct Answer is:A
Let T∝Sxryρz
by subsituting the dimension of [T]=[T]
[S]=[MT−2],[r]=[L],[ρ]=[ML−3]
and by comparing the power of both sides
x=−12,y=32,z=12
So T∝√ρr3S⇒T=k√ρ3S
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Multiple correct Answer Type
54 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
Similar Questions
The time period (T) of small oscillations of the surface of a liquid drop depends on its surface tension (s), the density (ρ) of the liquid and it's mean radius (r) as T=csxpyrz. If in the measurement of the mean radius of the drop, the error is 2%, the error in the measurement of surface tension and density both are of 1%. Find the percentage error in measurement of the time period.
View SolutionA spherical liquid drop is placed on a horizontal plane . A small distrubance cause the volume of the drop to oscillate . The time period oscillation (T) of the liquid drop depends on radius (r) of the drop , density (ρ) and surface tension tension (S) of the liquid. Which amount the following will be be a possible expression for T (where k is a dimensionless constant)?
View SolutionTime period of an oscillating drop of radius r, density ρ and surface tension T is t=k√ρr5T. Check the correctness of the relation
View SolutionThe time period of oscillation T of a small drop of liquid under surface tension depends upon the density ρ, the radius r and surface tension σ. Using dimensional analysis show that T∝√ρr3σ
View SolutionThe time period of a soap bubble is T which depneds on pressure p density d and surface tension s then the relation for T is
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
View SolutionA certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
View SolutionSelect the incorrect option (T = surface tension, R = radius of drop, bubble, meniscus)
View SolutionA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
View Solution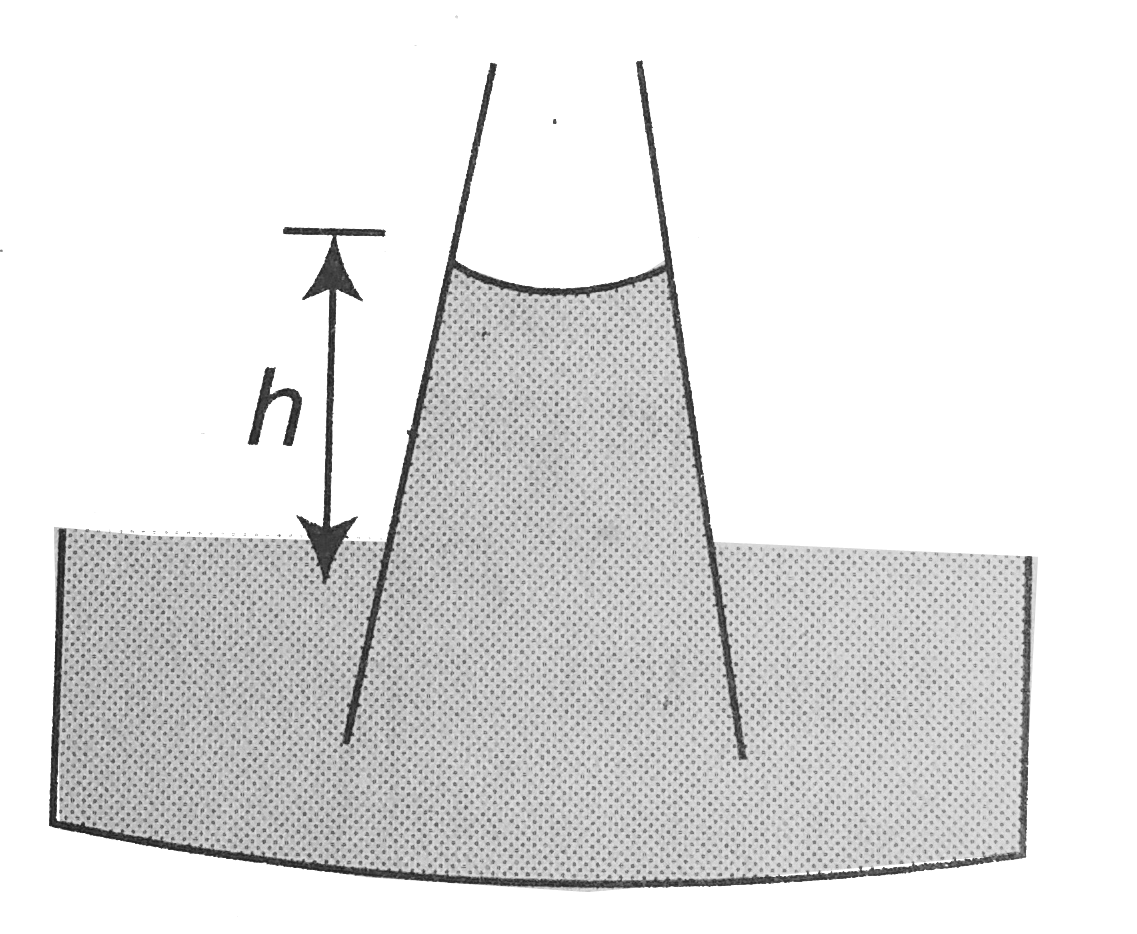
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View Solution
