An athlletic coach told his team that muscle times speed equals power. What dimesions does he view for muscle?
MLT−2
ML2T−2
MLT−2
L
The correct Answer is:A
To solve the problem, we need to find the dimensions of "muscle" based on the relationship given by the athletic coach: muscle times speed equals power. Let's break this down step by step.
Step 1: Understand the relationship
The coach states that:
Muscle×Speed=Power
Let’s denote the dimension of muscle as (M).
Step 2: Write the dimensions of speed
Speed is defined as distance traveled per unit time. The dimension of speed can be expressed as:
Speed=DistanceTime=LT
Thus, the dimension of speed is:
(Speed)=(L)(T−1)
Step 3: Write the dimensions of power
Power is defined as the rate of doing work or energy transfer per unit time. The dimension of power can be expressed as:
Power=WorkTime
The dimension of work (or energy) is:
Work=Force×Distance=(M)(L)(T−2)(L)=(M)(L2)(T−2)
Thus, the dimension of power is:
(Power)=(M)(L2)(T−2)(T)=(M)(L2)(T−3)
Step 4: Set up the equation with dimensions
From the relationship given:
(M)×(Speed)=(Power)
Substituting the dimensions we have:
(M)×(L)(T−1)=(M)(L2)(T−3)
Step 5: Solve for the dimension of muscle
Now we can express this as:
(M)×(L)(T−1)=(M)(L2)(T−3)
To isolate the dimension of muscle, we can rearrange the equation:
(M)=(M)(L2)(T−3)(L)(T−1)
Step 6: Simplify the right side
(M)=(M)×(L2)(L)×(T−3)(T−1)
This simplifies to:
(M)=(M)×(L2−1)(T−3+1)=(M)×(L1)(T−2)
Step 7: Cancel out the common dimension
Since we have (M) on both sides, we can cancel it out (assuming (M)≠0):
1=(L1)(T−2)
Thus, the dimension of muscle can be expressed as:
(M)=(L1)(T−2)
Final Answer
Thus, the dimension of muscle is:
(M)(L1)(T−2)
The coach states that:
Muscle×Speed=Power
Speed is defined as distance traveled per unit time. The dimension of speed can be expressed as:
Speed=DistanceTime=LT
Thus, the dimension of speed is:
(Speed)=(L)(T−1)
Power is defined as the rate of doing work or energy transfer per unit time. The dimension of power can be expressed as:
Power=WorkTime
The dimension of work (or energy) is:
Work=Force×Distance=(M)(L)(T−2)(L)=(M)(L2)(T−2)
Thus, the dimension of power is:
(Power)=(M)(L2)(T−2)(T)=(M)(L2)(T−3)
From the relationship given:
(M)×(Speed)=(Power)
Substituting the dimensions we have:
(M)×(L)(T−1)=(M)(L2)(T−3)
Now we can express this as:
(M)×(L)(T−1)=(M)(L2)(T−3)
To isolate the dimension of muscle, we can rearrange the equation:
(M)=(M)(L2)(T−3)(L)(T−1)
(M)=(M)×(L2)(L)×(T−3)(T−1)
This simplifies to:
(M)=(M)×(L2−1)(T−3+1)=(M)×(L1)(T−2)
Since we have (M) on both sides, we can cancel it out (assuming (M)≠0):
1=(L1)(T−2)
Thus, the dimension of muscle can be expressed as:
(M)=(L1)(T−2)
Thus, the dimension of muscle is:
(M)(L1)(T−2)
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Multiple correct Answer Type
54 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
Similar Questions
If 'muscle times speed equals power', then what is the ratio of the SI unit and the CGS unit of muscle?
View SolutionA cheetah, on seeing a prey, moves towards him at a very high speed. What causes the movement of his muscles ? How does the chemistry of cellular components of muscle change during this event ?
View Solution
Knowledge Check
A tradesman marks his goods at 35 percent above the cost price and then allows purchasers a discount of 15 percent. What profit percent does he save ?
A14.75%B13.95%C24.75%D25%A certain homeowner uses a gas edger to clean up his lawn every time he mows. If the edger uses 160 milliliters of fuel each time, what is the maximum number of times the homeowner can edge his lawn with 8 litres of fuel?( 1 liter = 1,000 milliliters)
A5B50C100D1000
Ravi walks at a uniform speed of 4 km per hour . How much time does he take to cover 600 metres ?
View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
View SolutionA person can see clearly only upto a distance of 25cm. He wants to read a book placed at a distance of 50cm. What kind of lens does he require for his spectacles and what must be its power ?
View SolutionA man is coming down an incline of angle 30∘. When he walks with speed 2(√3)ms−1 he has to keep his umbrella vertical to protect himself from rain. The actual speed of rain is 5ms−1. At angle with vertical should he keep his umbrella when he is at rest so that he does not getb drenched ?
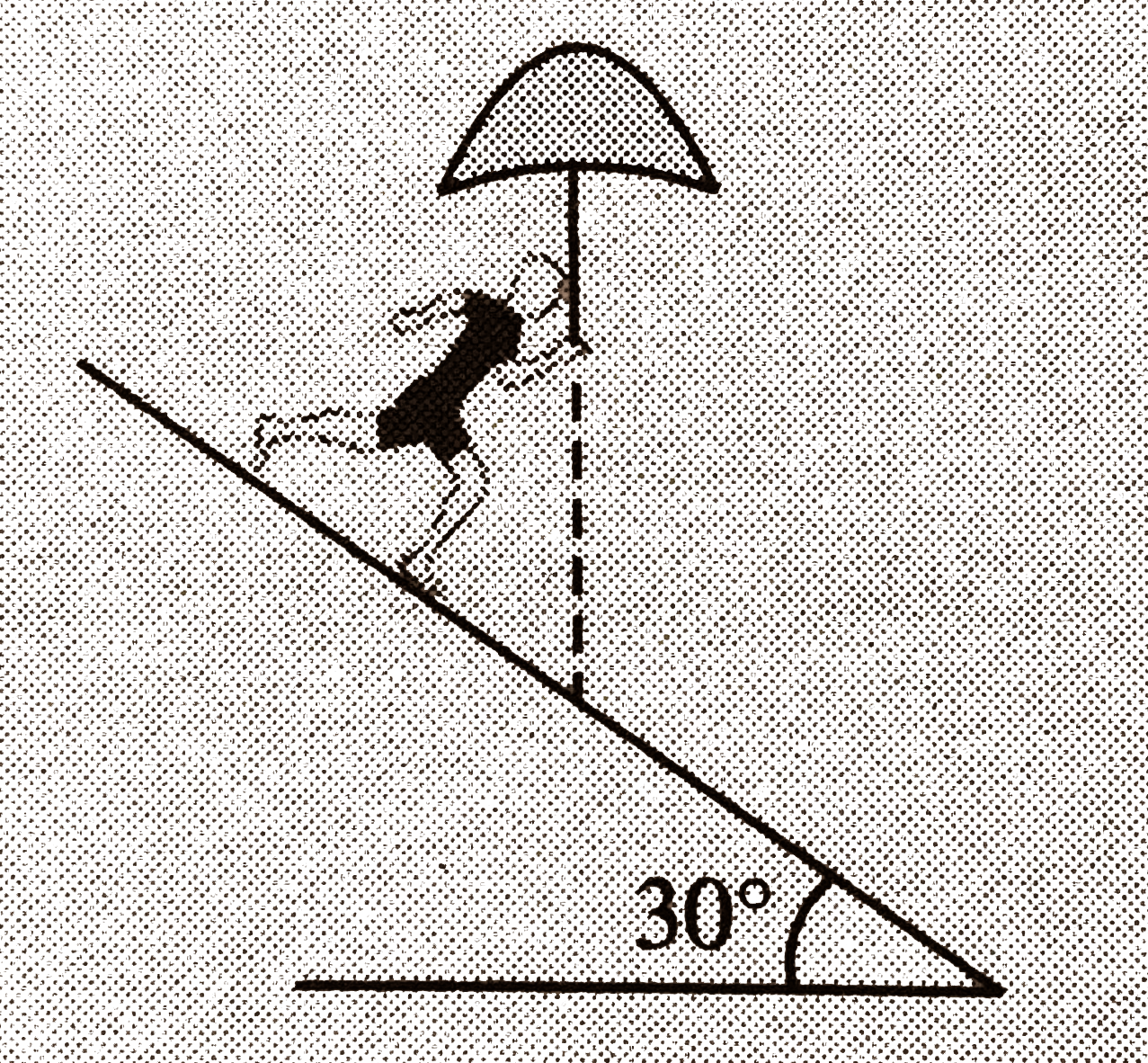 .
.
View SolutionA 90−kg man runs up an escalator while it is not in operation in 10s. What is the average power developed by the man. Suppose the escalator is running so that the escalator steps move at a speed of 0.5m−1. What is then the power developed by the man as seen by the ground reference if he moves at the same speed relative to the escalator steps as he did when the escalator is not in operation?

View SolutionA man's age is three times that of his son and in twelve years he will be twice as old as his son would be. What are their present ages?
View Solution
