In S=a+bt+ct2. S is measured in metres and t in seconds. The unit of c is
None
m
ms−1
ms−2
The correct Answer is:D
To find the unit of c in the equation S=a+bt+ct2, we can follow these steps:
Step 1: Identify the units of each term in the equation
The equation consists of four terms: S, a, bt, and ct2. Since all terms in the equation must have the same dimensions, we will start by identifying the units of S and t.
- The unit of S (displacement) is measured in meters (m).
- The unit of t (time) is measured in seconds (s).
Step 2: Analyze the terms
1. Term 1: S has units of meters (m).
2. Term 2: a must also have units of meters (m) since it is added to S.
3. Term 3: bt must also have units of meters (m). Since t is in seconds (s), we can express the units of b as follows:
Units of b=Units of SUnits of t=ms(units of b is m/s)
4. Term 4: ct2 must also have units of meters (m). Since t2 has units of seconds squared (s²), we can express the units of c as follows:
Units of c=Units of SUnits of t2=ms2
Step 3: Finalize the unit of c
Thus, the unit of c can be expressed as:
Units of c=m⋅s−2
Conclusion
The unit of c is meters per second squared (m/s²).
The equation consists of four terms: S, a, bt, and ct2. Since all terms in the equation must have the same dimensions, we will start by identifying the units of S and t.
- The unit of t (time) is measured in seconds (s).
1. Term 1: S has units of meters (m).
2. Term 2: a must also have units of meters (m) since it is added to S.
3. Term 3: bt must also have units of meters (m). Since t is in seconds (s), we can express the units of b as follows:
Units of b=Units of SUnits of t=ms(units of b is m/s)
Units of c=Units of SUnits of t2=ms2
Thus, the unit of c can be expressed as:
Units of c=m⋅s−2
The unit of c is meters per second squared (m/s²).
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Multiple correct Answer Type
54 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
Similar Questions
The position of the particle moving along Y-axis is given as y=At2−Bt3, where y is measured in metre and t in second. Then, the dimensions of B are
View SolutionThe position of the particle moving along Y-axis is given as y=At2−Bt3, where y is measured in metre and t in second. Then, the dimensions of B are
View SolutionA particle moves along the curve y=x22. Here x varies with time as x=t22. Where x and y are measured in metres and t in seconds. At t=2s, the velocity of the particle (in ms−1) is
View SolutionA particle moves along the positive branch of the curve y=x22 where x=t22,x and y are measured in metres and t in second. At t=2s, the velocity of the particle is
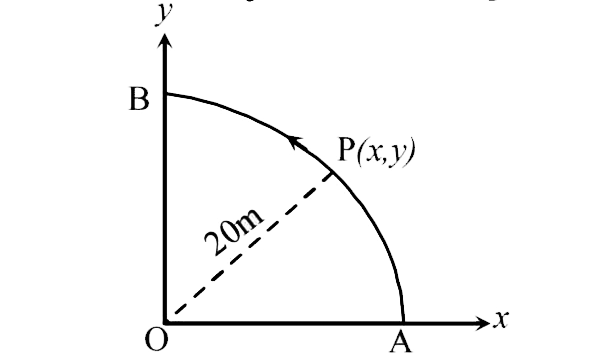
View SolutionA point p moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length s=t3+5 , where s is in metres and t is in seconds . The radius of the path is 20m . The acceleration of 'P' when t=2s is nearly .
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionA car moves along a straight line whose equation of motion is given by
s=12t+3t2−2t3
where s is in metres and t is in seconds. The velocity of the car at start will be :-
View SolutionThe x and y coordinates of a particle at any time t are given by x=2t+4t2andy=5t , where x and y are in metre and t in second. The acceleration of the particle at t = 5 s is
View SolutionThe displacement of a particle is moving by x=(t−2)2 where x is in metres and t in second. The distance covered by the particle in first 4 seconds is.
View Solution
