A point mass is subjected to two simultaneous sinusoidal displacements in x−direction,x1(t)=Asin(ω)tandx2(t)=Asin((ωt+2π3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mas to a complete rest. The values of (B) and (phi) are.
√2A,3π4
A,4π3
√3A,5π6
A,π3
The correct Answer is:B
To solve the problem, we need to analyze the given sinusoidal displacements and find the values of B and ϕ such that the total displacement brings the mass to rest. Here’s a step-by-step solution:
Step 1: Understanding the Given Displacements
We have two sinusoidal displacements:
1. x1(t)=Asin(ωt)
2. x2(t)=Asin(ωt+2π3)
Step 2: Adding the Two Displacements
We need to find the resultant of x1 and x2. Since both displacements have the same amplitude A and a phase difference of 2π3 (or 120 degrees), we can use the formula for the resultant of two vectors with the same magnitude:
R=2Acos(θ2)
where θ=2π3.
Step 3: Calculating the Resultant Amplitude
Calculating R:
R=2Acos⎛⎝2π32⎞⎠=2Acos(π3)
cos(π3)=12
Thus,
R=2A⋅12=A
Step 4: Finding the Phase of the Resultant
The resultant phase angle ϕR can be found using the angle bisector theorem:
ϕR=θ2=120∘2=60∘ or π3 radians
So, the resultant displacement can be expressed as:
xR(t)=Asin(ωt+π3)
Step 5: Adding the Third Displacement
Now, we introduce the third displacement:
x3(t)=Bsin(ωt+ϕ)
We need the total displacement to be zero:
x1+x2+x3=0
This implies:
Asin(ωt+π3)+Bsin(ωt+ϕ)=0
Step 6: Setting Up the Equation
For the total to be zero, x3(t) must be equal to the negative of the resultant:
x3(t)=−Asin(ωt+π3)
Step 7: Comparing Amplitudes and Phases
From this, we can see that:
1. The amplitude B must equal A:
B=A
2. The phase ϕ must be:
ϕ=π3+π=4π3
Final Result
Thus, the values of B and ϕ are:
B=A,ϕ=4π3
We have two sinusoidal displacements:
1. x1(t)=Asin(ωt)
2. x2(t)=Asin(ωt+2π3)
We need to find the resultant of x1 and x2. Since both displacements have the same amplitude A and a phase difference of 2π3 (or 120 degrees), we can use the formula for the resultant of two vectors with the same magnitude:
Calculating R:
R=2Acos⎛⎝2π32⎞⎠=2Acos(π3)
cos(π3)=12
Thus,
R=2A⋅12=A
The resultant phase angle ϕR can be found using the angle bisector theorem:
ϕR=θ2=120∘2=60∘ or π3 radians
So, the resultant displacement can be expressed as:
xR(t)=Asin(ωt+π3)
Now, we introduce the third displacement:
x3(t)=Bsin(ωt+ϕ)
We need the total displacement to be zero:
x1+x2+x3=0
This implies:
Asin(ωt+π3)+Bsin(ωt+ϕ)=0
For the total to be zero, x3(t) must be equal to the negative of the resultant:
x3(t)=−Asin(ωt+π3)
From this, we can see that:
1. The amplitude B must equal A:
B=A
2. The phase ϕ must be:
ϕ=π3+π=4π3
Thus, the values of B and ϕ are:
B=A,ϕ=4π3
Topper's Solved these Questions
- ARCHIVES 2 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 2 VOLUME 6Exercise:Multiple Correct
Explore 22 Videos
- ARCHIVES 2 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 2 VOLUME 6Exercise:Comprehension
Explore 12 Videos
- ARCHIVES 2 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 2 VOLUME 6Exercise:True/False
Explore 4 Videos
- ARCHIVES 1 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 1 VOLUME 6Exercise:Integer
Explore 4 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
Similar Questions
A point mass is subjected to two simultaneous sinusoidal displacement in x-direction, x1(t)=Asinωt and x2(t)=Asin(ωt+2π/3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mass to a complete rest. The values of B and ϕ are :
View SolutionIf i1=3sinωtand(i2)=4cosωt, then (i3) is

View SolutionIn y= A sin ωt + A sin (ωt+(2π)/3) match the following table.
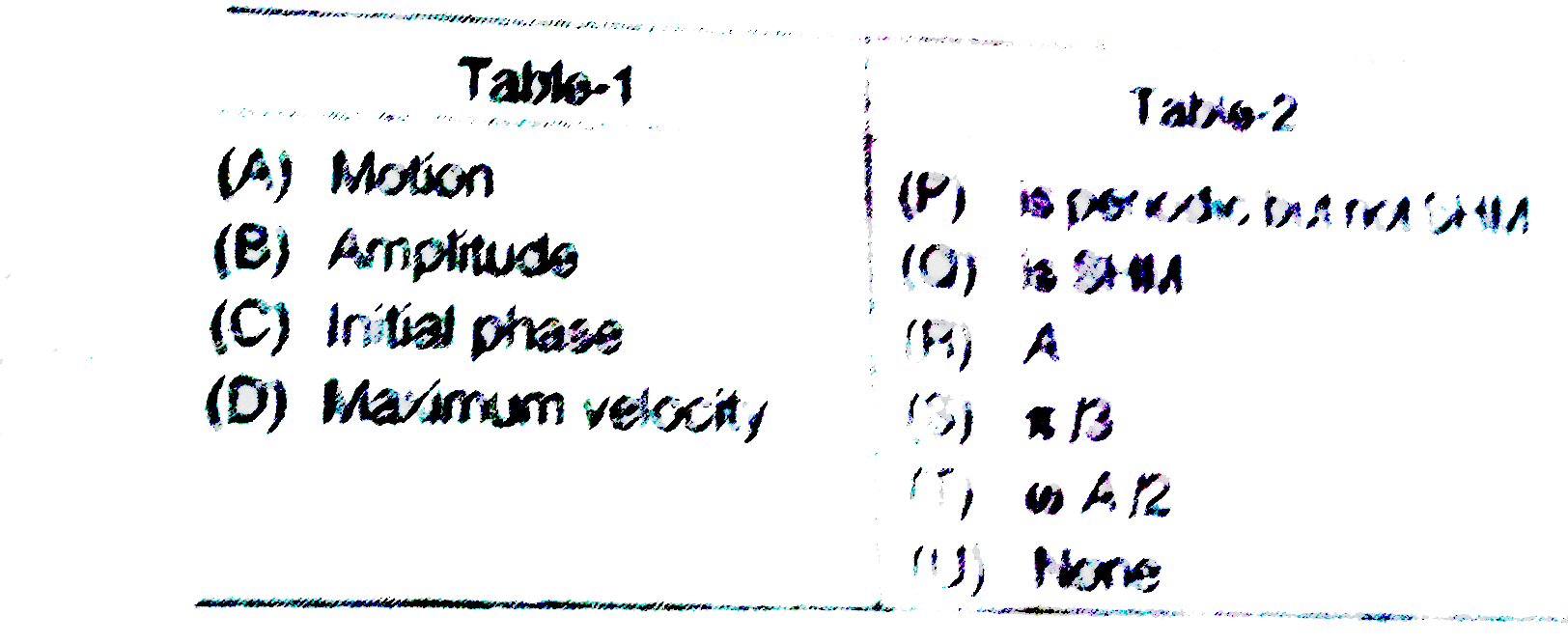
View SolutionFind the displacement equation of the simple harmonic motion obtained by combining the motion.
x1=2sinωt, x2=4sin(ωt+π6) and x3=6sin(ωt+π3)
View SolutionA partical is subjucted to two simple harmonic motions
x1=A1sinωt
and x2=A2sin(ωt+π/3)
Find(a) the displacement att=0, (b) the maximum speed of the partical and ( c) the maximum acceleration of the partical.
View Solutionx1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.
View Solutionx1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.
View SolutionFind time period of the function, y=sinωt+sin2ωt+sin3ωt
View SolutionWhen two displacement represented by y1=asin(ωt) and y2=bcos(ωt) are superimposed, the motion is
View SolutionTwo simple harmonic motions given by, x=asin(ωt+δ) and y=asin(ωt+δ+π2) act on a particle will be
View Solution

