In a standing wave experiment , a 1.2−kg horizontal rope is fixed in place at its two ends (x=0andx=2.0m) and made to oscillate up and down in the fundamental mode , at frequency of 5.0Hz. At t=0 , the point at x=1.0m has zero displacement and is moving upward in the positive direction of y−aξs with a transverse velocity 3.14m/s.
What is the correct expression of the standing wave equation ?
(0.1)sin(π/2)xsin(10π)t
(0.1)sin(π)xsin(10π)t
(0.05)sin(π/2)xcos(10π)t
(0.04)sin(π/2)xsin(10π)t
The correct Answer is:A
To derive the standing wave equation for the given problem, we will follow these steps:
Step 1: Determine the mass per unit length (μ) of the rope.
Given:
- Mass of the rope (m) = 1.2 kg
- Length of the rope (L) = 2.0 m
The mass per unit length (μ) is calculated as:
μ=mL=1.2kg2.0m=0.6kg/m
Step 2: Find the wavelength (λ) in the fundamental mode.
In the fundamental mode of a fixed string, the wavelength is given by:
λ2=L⟹λ=2L=2×2.0m=4.0m
Step 3: Calculate the wave speed (v).
The wave speed (v) can be calculated using the formula:
v=f⋅λ
Where:
- Frequency (f) = 5.0 Hz
- Wavelength (λ) = 4.0 m
Thus,
v=5.0Hz×4.0m=20.0m/s
Step 4: Calculate the tension (T) in the rope.
Using the relationship between wave speed, tension, and mass per unit length:
v=√Tμ⟹T=μv2
Substituting the values:
T=0.6kg/m×(20.0m/s)2=0.6×400=240N
Step 5: Determine the amplitude (A) of the wave.
At t=0, the transverse velocity (∂y∂t) is given as 3.14 m/s. The maximum transverse velocity is given by:
∂y∂t=ωA
Where ω=2πf:
ω=2π×5.0Hz=10πrad/s
Thus:
3.14=10πA⟹A=3.1410π≈0.1m
Step 6: Write the standing wave equation.
The general form of the standing wave equation is:
y(x,t)=Asin(kx)cos(ωt)
Where:
- k=2πλ=2π4=π2rad/m
Substituting the values of A, k, and ω:
y(x,t)=0.1sin(π2x)cos(10πt)
Final Answer:
The correct expression for the standing wave equation is:
y(x,t)=0.1sin(π2x)cos(10πt)
---
Given:
- Mass of the rope (m) = 1.2 kg
- Length of the rope (L) = 2.0 m
μ=mL=1.2kg2.0m=0.6kg/m
In the fundamental mode of a fixed string, the wavelength is given by:
λ2=L⟹λ=2L=2×2.0m=4.0m
The wave speed (v) can be calculated using the formula:
v=f⋅λ
Where:
- Frequency (f) = 5.0 Hz
- Wavelength (λ) = 4.0 m
v=5.0Hz×4.0m=20.0m/s
Using the relationship between wave speed, tension, and mass per unit length:
v=√Tμ⟹T=μv2
Substituting the values:
T=0.6kg/m×(20.0m/s)2=0.6×400=240N
At t=0, the transverse velocity (∂y∂t) is given as 3.14 m/s. The maximum transverse velocity is given by:
∂y∂t=ωA
Where ω=2πf:
ω=2π×5.0Hz=10πrad/s
Thus:
3.14=10πA⟹A=3.1410π≈0.1m
The general form of the standing wave equation is:
y(x,t)=Asin(kx)cos(ωt)
Where:
- k=2πλ=2π4=π2rad/m
y(x,t)=0.1sin(π2x)cos(10πt)
The correct expression for the standing wave equation is:
y(x,t)=0.1sin(π2x)cos(10πt)
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Integer
9 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct Answer Type
56 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning
6 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
In a standing wave experiment , a 1.2−kg horizontal rope is fixed in place at its two ends (x=0andx=2.0m) and made to oscillate up and down in the fundamental mode , at frequency of 5.0Hz. At t=0 , the point at x=1.0m has zero displacement and is moving upward in the positive direction of y−aξs with a transverse velocity 3.14m/s.
Tension in the rope is
View SolutionIn a standing wave experiment , a 1.2−kg horizontal rope is fixed in place at its two ends (x=0andx=2.0m) and made to oscillate up and down in the fundamental mode , at frequency of 5.0Hz. At t=0 , the point at x=1.0m has zero displacement and is moving upward in the positive direction of y−aξs with a transverse velocity 3.14m/s.
Speed of the participating travelling wave on the rope is
View SolutionA wave travelling in positive X-direction with A=0.2m has a velocity of 360m/sec if λ=60m, then correct exression for the wave is
View SolutionA wave travelling in positive X-direction with A=0.2m has a velocity of 360m/sec if λ=60m, then correct exression for the wave is
View SolutionA particle A of mass 10/7kg is moving in the positive direction of x-axis. At initial position x=0, its velocity is 1ms−1, then its velocity at x=10m is (use the graph given)
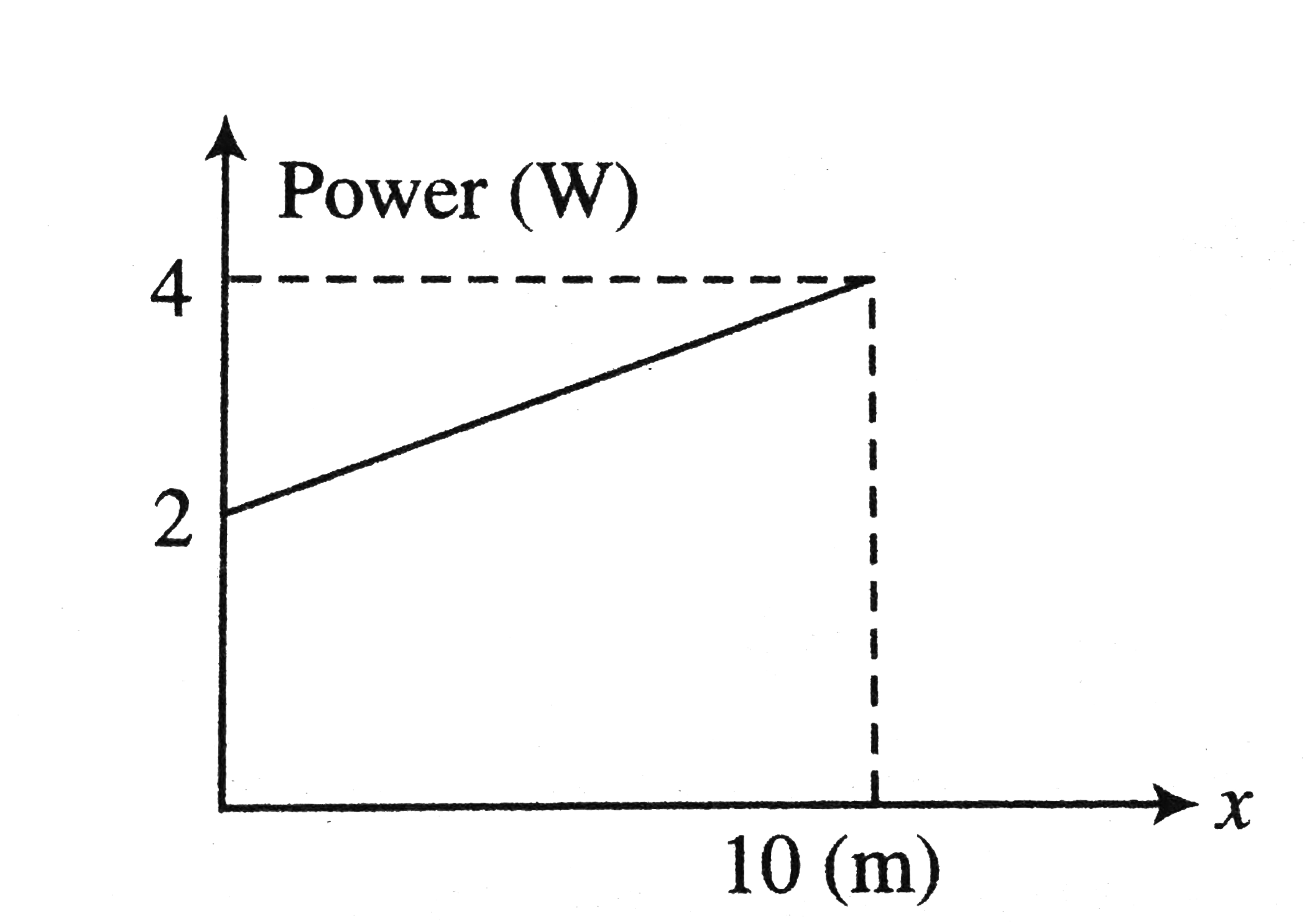
View SolutionA particle A of mass 10/7kg is moving in the positive direction of x−aξs. At initial position x=0, its velocity is 1ms−1, then its velocity at x=10m is (use the graph given)

View SolutionThe standing wave pattern shown in the tube has a wave speed of 5.0ms−1. What is the frequency of the standing wave [ in Hz approx.] ?

View SolutionA particle located at position x=0, at time t=0, starts moving along the positive x-direction with a velocity v2=αx (where alpha is a positive constant). The displacement of particle is proportional to
View SolutionA 100 Hz sinusoidal wave is travelling in the positve x - direaction along a string with a linear mass density of 3.5×10−3kgm−1 and a tension of 35 N. At time t =0 ,the point x=0 has zero displacment and the slope of the string is π/20then select the wrong alternative.
View SolutionTransverse waves on a srting have speed 12.0m/s, amplitude 0.05m and wavelength 0.4m. The waves travel in the +x−direction and at t=0 the x=0 end of the string has zero displacement and is moving upwards.
(a) Write a wave function describing the wave.
(b) Find the transverse displacement of a point at x=0.25m at time t=0.15s.
( c ) How much time must elapse from the instant in part (b) until the point at x=0.25m has zero dispacement?
View Solution
