A long string having a cross- sectional area 0.80mm2 and density 12.5gcm−3 is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency fo 20Hz. At t = 0. the source is at a maximujm displacement y= 1.0 cm. (a) Write the equation for the wave. (b) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s ? (c) What is the velocity of this particle at this instant ?
y=(1.0cm)cos[(40πs−1)t−{(π/2m−1x}]
y=(1.0cm)cos[(40πs−1)t+{(π/2m−1x}]
y=(1.0cm)cos[(40πs−1)t−{(π/4m−1x}]
y=(1.0cm)cos[(40πs−1)t+{(π/4m−1x}]
The correct Answer is:a
Mass per unit length of the string is
μ=Ad=(0.80mm2)×(12.5g/cm3)=0.01kg/m
=(0.80×10−6m2)×(12.5×103)=0.01kg/m
speed of transverse waves produced in the string
v=√Tμ=√640.01kg/m=80m/s
the amplitude of the source is a=1.0cm and the frequency is f=20Hz. the angular frequency is ω=2πf=40π/s.
also at t=0, the displacement is equal to its amplitute, i.e., at t=0,y=a. the equation of motion of the source is, therefore,
y=(1.0cm)cos[(40πs−1)t] ...(1)
the equation of the wave travelling on the string along the positive X−axis is obtained by replacing t by [t−(x/v)] in Eq. (i). It is, therefore,
y=(1.0cm)cos[940πs−1){t−(x/v)}x]
=(1.0cm)cos[(40πs−1)t−{(π/2)m−1)}x]
the displacement of the particle at x=50cm at time t=0.05s is obtained from Eq. (ii).
y=(1.0cm)cos[(40πs−1)(0.05s)
−{(π/2)m−1(0.5m)]
=(1.0cm)cos[2π−(π/4)]
=1.0cm/√2=0.71cm
the velocity of the particle at position x at time t is also obtained from Eq. (ii).
V=∂y∂t=−(1.0cm)(40πs−1)t−{(π/2)m−1}x]
=−(40πcms)sin(2π−π4)
=−40π√2cm/s=−89cm/s
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Assertion-Reasoning
6 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A sinusoidal wave is traveling on a string with speed 40 cm/s. The displacement of the particle of the string at x = 10 cm varies with time according to
y = (5.0cm) sin(1.0−4.0s−1)t)The linear density of the string is 4.0 g/cm
View SolutionA particle vibrates harmonically at a frequency of 0.5 Hz. At the initial moment it is in an equilibrium position moving at a speed of 20 cm/s. Write down the equation of the vibrations.
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
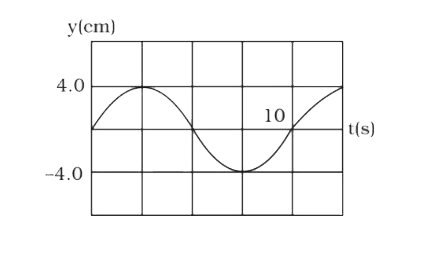
Q. The velocity of propagation of the wave is ?
View SolutionThe equation for a wave travelling in x-direction 0n a string is
y=(3.0cm)sin[(3.14cm−1x−(314s−1t]
(a) Find the maximum velocity of a particle of the string.
(b) Find the acceleration of a particle at x=6.0cm at time t=0.11s
View SolutionThe equation for a wave travelling in x-direction on a string is y =(3.0cm)sin[(3.14cm−1x−(314s−1)t] (a) Find the maximum velocity of a particle of the string. (b) Find the acceleration of a particle at x =6.0 cm at time t = 0.11 s.
View SolutionA string of density 7.5gcm−3 and area of cross - section 0.2mm2 is stretched under a tension of 20 N. When it is plucked at the mid-point, the speed of the transverse wave on the wire is
View SolutionA string vibrates in its first normal mode with a frequency of 220 vibrations /s. The vibrating segment is 70.0 cm long and has a mass of 1.20g.
(a) Find the tension in the string.
(b) Determine the frequency of vibration when the string vibrates in three segments.
View SolutionA string of length 1 m and mass 5 g is fixed at both ends. The tension in the string is 8.0 N. The string is set into vibration using an external vibrator of frequency 100 Hz. The separation between successive nodes on the string is close to :
View SolutionThe equation of a wave travelling on a string is y=(0.10mm)sin[(31.4m−1)x+(314s−1)t]
(a) In which direction does the travel?
(b) Find the wave speed, the wavelength and the frequency of the wave.
( c ) What is the maximum displacement and the maximum speed of a portion of the string?
View SolutionA pulse is started at a time t=0 along the +x directions an a long, taut string. The shaot of the puise at t=0 is given by funcation y with
y=⎧⎪ ⎪⎨⎪ ⎪⎩x4+1for−4<x≤0−x+1for0<x<10 otherwise
here y and x are in centimeters. The linear mass density of the string is 50g/m and it is under a tension of 5N,
The vertical displacement of the particle of the string at x=7cm and t=0.01s will be
View Solution
