A sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at x=2 cm is found at its mean position and it is moving in positive y-direction at t=1 s. the amplitude of the wave, the wavelength and the angular frequency of the wave are 0.1m,π/4m and 4πrad/s, respectively.
The equation of the wave is
y=0.1sin(4π(t−1)+8(x−2))
y=0.1sin((t−1)−(x−2))
y=0.1sin(4π(t−1)−8(x−2))
none of these
The correct Answer is:a
To find the equation of the sinusoidal wave propagating in the negative x-direction, we will follow these steps:
Step 1: Identify the given parameters
- Amplitude A=0.1m
- Wavelength λ=π4m
- Angular frequency ω=4πrad/s
- Position of the particle x=2cm=0.02m (convert cm to m)
- Time t=1s
Step 2: Calculate the wave number k
The wave number k is given by the formula:
k=2πλ
Substituting the value of λ:
k=2ππ4=8m−1
Step 3: Write the general form of the wave equation
For a wave propagating in the negative x-direction, the wave equation is given by:
y(x,t)=Asin(ωt+kx+ϕ)
Step 4: Determine the phase constant ϕ
We know that at x=0.02m and t=1s, the particle is at its mean position (which corresponds to y=0) and moving in the positive y-direction. This means the sine function must be at its maximum slope, which occurs at sin(ωt+kx+ϕ)=0.
Since the particle is at the mean position, we can set:
ωt+kx+ϕ=0
Substituting t=1s and x=0.02m:
4π(1)+8(0.02)+ϕ=0
4π+0.16+ϕ=0
ϕ=−4π−0.16
Step 5: Substitute the values into the wave equation
Now we can write the wave equation:
y(x,t)=0.1sin(4πt+8x−(4π+0.16))
Simplifying this gives:
y(x,t)=0.1sin(4πt+8x−4π−0.16)
y(x,t)=0.1sin(8x+4πt−4π−0.16)
Final Equation
Thus, the equation of the wave is:
y(x,t)=0.1sin(4πt+8x−4π−0.16)
- Amplitude A=0.1m
- Wavelength λ=π4m
- Angular frequency ω=4πrad/s
- Position of the particle x=2cm=0.02m (convert cm to m)
- Time t=1s
The wave number k is given by the formula:
k=2πλ
Substituting the value of λ:
k=2ππ4=8m−1
For a wave propagating in the negative x-direction, the wave equation is given by:
y(x,t)=Asin(ωt+kx+ϕ)
We know that at x=0.02m and t=1s, the particle is at its mean position (which corresponds to y=0) and moving in the positive y-direction. This means the sine function must be at its maximum slope, which occurs at sin(ωt+kx+ϕ)=0.
ωt+kx+ϕ=0
4π(1)+8(0.02)+ϕ=0
4π+0.16+ϕ=0
ϕ=−4π−0.16
Now we can write the wave equation:
y(x,t)=0.1sin(4πt+8x−(4π+0.16))
Simplifying this gives:
y(x,t)=0.1sin(4πt+8x−4π−0.16)
y(x,t)=0.1sin(8x+4πt−4π−0.16)
Thus, the equation of the wave is:
y(x,t)=0.1sin(4πt+8x−4π−0.16)
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Assertion-Reasoning
6 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at x=2 cm is found at its mean position and it is moving in positive y-direction at t=1 s. the amplitude of the wave, the wavelength and the angular frequency of the wave are 0.1m,π/4m and 4πrad/s, respectively.
The speed of particle at x=2m and t=1s is
View SolutionFigure shows a plot of the transverse displacements of the particles of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20cms−1. Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.
 .
.
View SolutionFigure shows a plot of the transverse displacement of the particle of a string at t=0 through which a travelling wave is passing in the positive in the positive x-direction. The wave speed is 20cm/s. Find (a) the amplitude (b) the wavelength (c) the wave number and (d) the frequency of the wave.

View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
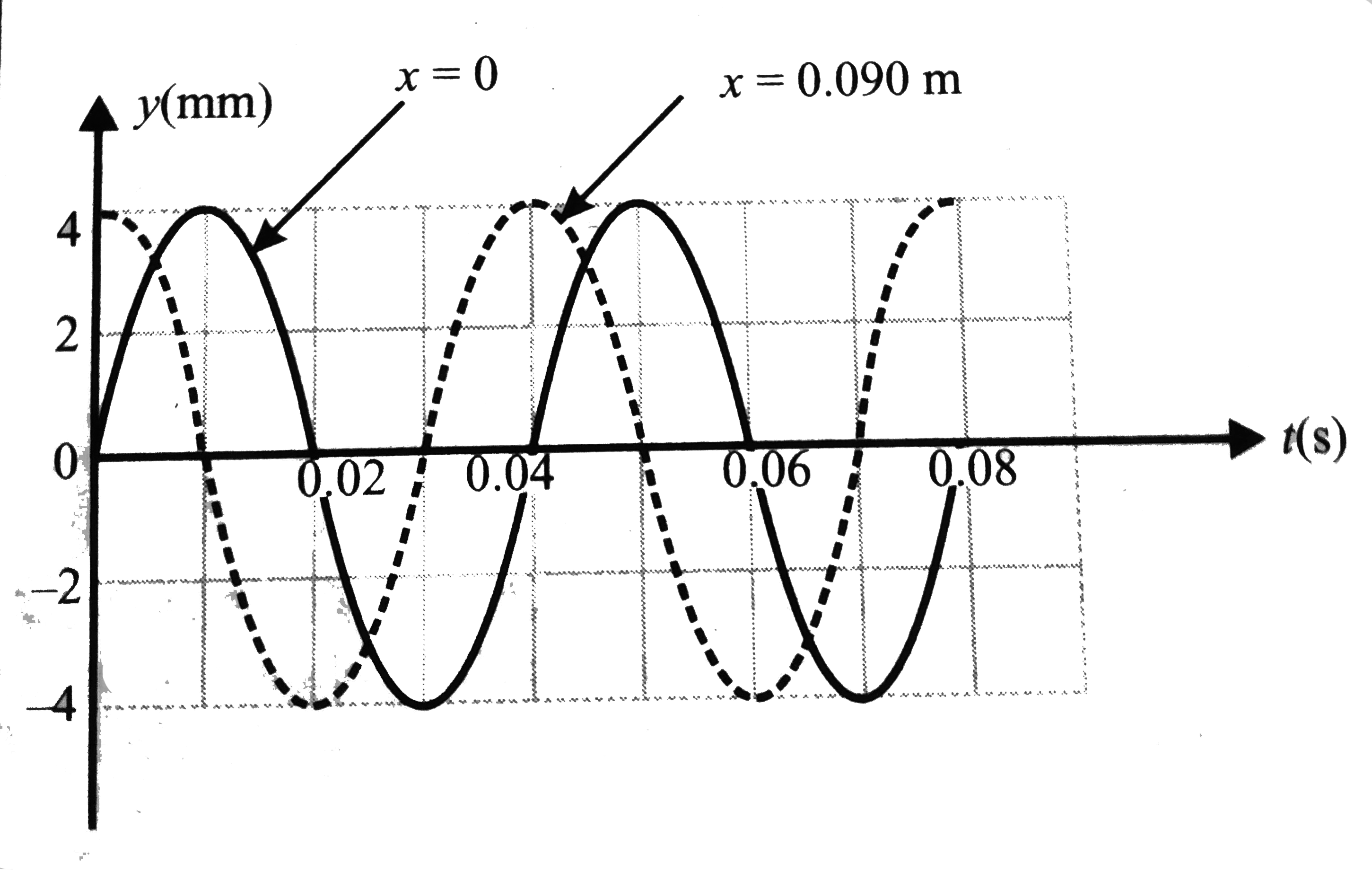
View SolutionA sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?
View SolutionThe equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View SolutionA transverse wave of amplitude 2 m, wavelength 4 m and frequency 6 Hz is propagating in a string toward positive y-direction. The equation of the wave may be (y is in m and t is in s)
View SolutionA sinusoidal wave trsvelling in the positive direction on a stretched string has amplitude 2.0cm, wavelength 1.0m and velocity 5.0m/s. At x=0 and t=0 it is given that y=0 and ∂y∂t<0. Find the wave function y(x,t).
View Solution
