A horizontal spring -block system of mass 2kg executes S.H.M when the block is passing through its equilibrium position an object of mass 1kg is put on it the two move together The new amplitude of vibration is (A being its initial amplitude)
√23A
√32A
√2A
A√2
The correct Answer is:A
To solve the problem of finding the new amplitude of the spring-block system after an additional mass is placed on it, we can follow these steps:
1. Identify the Initial Conditions:
- The initial mass of the block, m1=2kg.
- The initial amplitude of vibration, A.
- The additional mass placed on the block, m2=1kg.
- The total mass after adding the second block, m=m1+m2=2kg+1kg=3kg.
2. Conservation of Momentum:
- When the additional mass is placed on the block at the equilibrium position, the momentum of the system is conserved.
- Let the initial velocity of the 2 kg block be v. After the 1 kg mass is added, let the new velocity be v′.
- By conservation of momentum:
m1v=(m1+m2)v′
2v=3v′⇒v′=23v
3. Kinetic Energy and Potential Energy Relation:
- The total mechanical energy in the system is conserved. The kinetic energy at the equilibrium position is equal to the potential energy at the extreme position.
- Initially, the kinetic energy is given by:
KEinitial=12m1v2=12⋅2⋅v2=v2
- After adding the mass, the kinetic energy becomes:
KEfinal=12(m1+m2)v′2=12⋅3⋅(23v)2=12⋅3⋅49v2=23v2
4. Relate Kinetic Energy to Amplitude:
- The potential energy at the extreme position is given by:
PE=12kA2
- Since the total energy is conserved:
KEinitial=PEinitial⇒v2=12kA2
- For the new mass:
KEfinal=PEfinal⇒23v2=12kA′2
5. Setting the Equations Equal:
- From the equations for kinetic energy:
v2=12kA2and23v2=12kA′2
- Substitute v2 from the first equation into the second:
23⋅12kA2=12kA′2
- Cancel 12k from both sides:
23A2=A′2
6. Solve for the New Amplitude:
- Taking the square root of both sides:
A′=A√23
Final Answer:
The new amplitude of vibration after adding the mass is:
A′=A√23
- The initial mass of the block, m1=2kg.
- The initial amplitude of vibration, A.
- The additional mass placed on the block, m2=1kg.
- The total mass after adding the second block, m=m1+m2=2kg+1kg=3kg.
- When the additional mass is placed on the block at the equilibrium position, the momentum of the system is conserved.
- Let the initial velocity of the 2 kg block be v. After the 1 kg mass is added, let the new velocity be v′.
- By conservation of momentum:
m1v=(m1+m2)v′
2v=3v′⇒v′=23v
- The total mechanical energy in the system is conserved. The kinetic energy at the equilibrium position is equal to the potential energy at the extreme position.
- Initially, the kinetic energy is given by:
KEinitial=12m1v2=12⋅2⋅v2=v2
- After adding the mass, the kinetic energy becomes:
KEfinal=12(m1+m2)v′2=12⋅3⋅(23v)2=12⋅3⋅49v2=23v2
- The potential energy at the extreme position is given by:
PE=12kA2
- Since the total energy is conserved:
KEinitial=PEinitial⇒v2=12kA2
- For the new mass:
KEfinal=PEfinal⇒23v2=12kA′2
- From the equations for kinetic energy:
v2=12kA2and23v2=12kA′2
- Substitute v2 from the first equation into the second:
23⋅12kA2=12kA′2
- Cancel 12k from both sides:
23A2=A′2
- Taking the square root of both sides:
A′=A√23
The new amplitude of vibration after adding the mass is:
A′=A√23
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A horizontal spring block system of mass M executes simple harmonic motion. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration. Given, k is the spring constant of the system.
View SolutionA horizontal spring is connedted to a mass M. It exectues simple harmonic motion. When the mass M passes through its mean position, an object of mass m is put on it ans the two move together. The ratio of frequencies before and after will be-
View SolutionA block of mass M attached to the free end of a spring of force constant k is nounted on a smooth horizontal table as shown in figure.
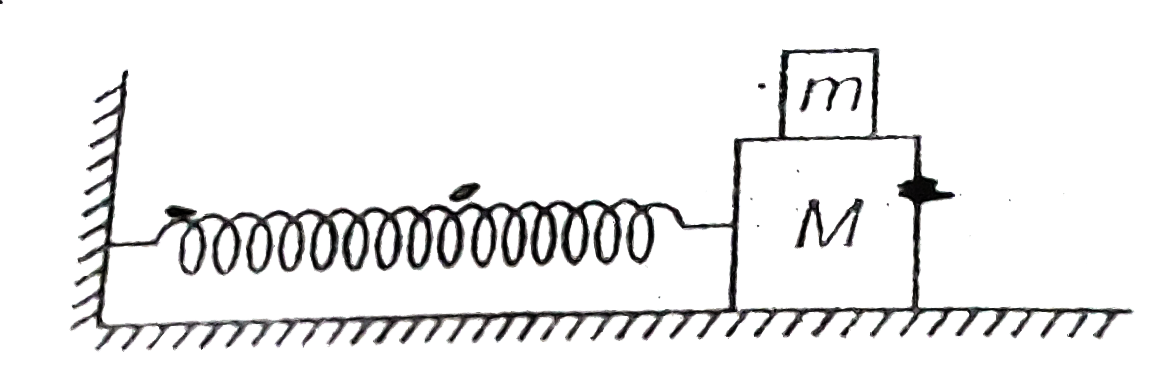
The block executes SHM with amplitude A and frequency f . If an object of mass m is put on it, when the block is passing through its equilibium position and the two move together ,then what is the new amplitude and frequency of vibration?
View SolutionA mass M, attached to a horizontal spring, excutes SHM with a amplitude A1. When the mass M passes through its mean position then a smaller mass m is placed over it and both of them move together with amplitude A2, the ratio of (A1A2) is :
View SolutionA mass m1=1kg connected to a horizontal spring performs S.H.M. with amplitude A. While mass m1 is passing through mean position another mass m2=3kg is placed on it so that both the masses move together with amplitude A1. The ratio of A1A is (pq)1/2, where p and q are the smallest integers. Then what is the value of p+q?
View SolutionA block with mass M attached to a horizontal spring with force constant k is moving with simple harmonic motion having amplitude A1. At the instant when the block passes through its equilibrium position a lump of putty with mass m is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.
View SolutionA block with mass M attached to a horizontal spring with force constant k is moving with simple harmonic motion having amplitude A1. At the instant when the block passes through its equilibrium position a lump of putty with mass m is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.
View SolutionA particle of mass 2kg executing SHM has amplitude 20cm and time period 1s. Its maximum speed is
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
View SolutionIn the figure shown, the block A of mass m collides with the identical block B and after collision they stick together. Calculate the amplitude of resulatant vibration.
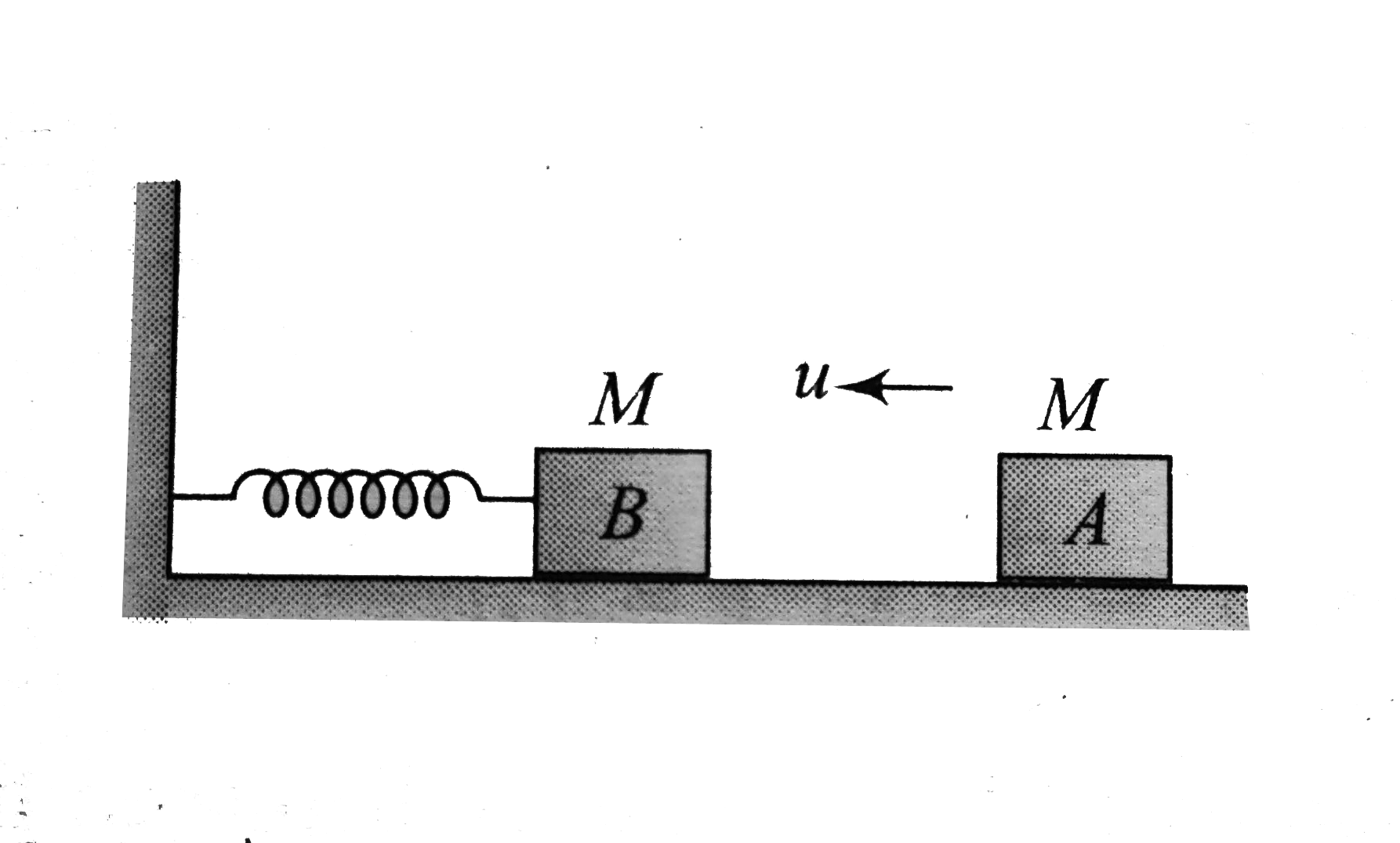
View Solution
