Question

Two springs with negligible massess and force constant of $k_1=200N{m}^{-1}$ and $k_2=160N{m}^{-1}$ are attached to the block of mass m = 10kg as shown in the figure. Initially the block is at rest at the equilibrium position the block is at rest at the equilibrium position nor compressed. At time t=0, sharp impulse of 50 N-s is given to the block.

Options

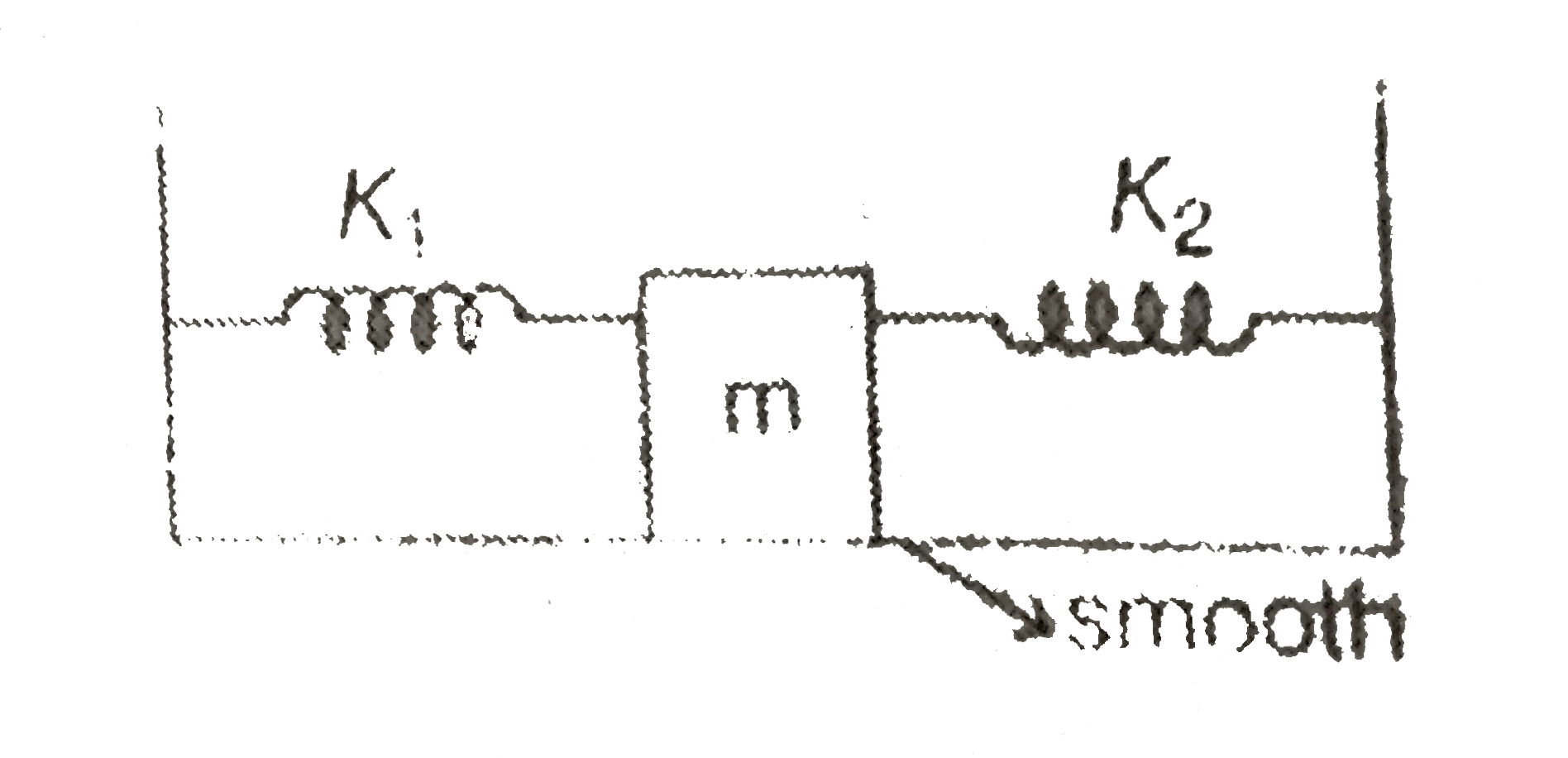
A. Period of oscillations for the mass m is `(pi)/(6)`s.
B. Maximum velocity of the mass m during its oscillation is `10(m)/(s)`
C. Data are insufficient to determine maximum velocity.
D. Amplitude of oscillation is `0.83m`.

Answer

D

Explanation

`T=2pisqrt((m)/(K_1+K_2))=2pisqrt((10)/(360))=(pi)/(3)s`
the maximum velocity is always at equilibrium position since at any other point there will be a restoring force at temting to slow the mass.
`V_("mass")=("impulse")/("mass")=(50)/(10)=5(m)/(s)impliesomega=(2pi)/(T)=6(rad)/(s)`
`impliesA=`amplitude`=(V_(max))/(omega)=(5)/(6)=0.83m`