Question

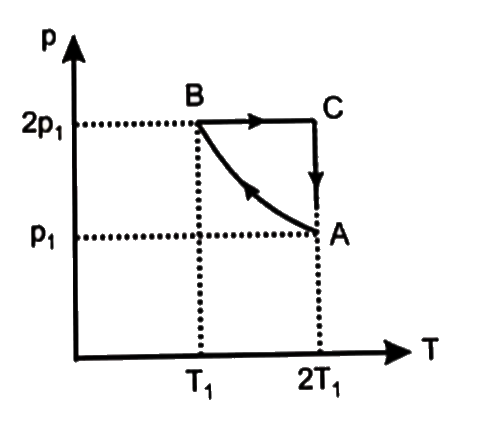
A reversible heat engine carries ${\displaystyle 1mol}$ of an ideal monatomic gas around the cycle ${\displaystyle ABCA}$, as shown in the diagram. The process ${\displaystyle BC}$ is adiabatic. Call the processes ${\displaystyle AB,BC}$ and ${\displaystyle CA}$ as ${\displaystyle 1,2}$ and ${\displaystyle 3}$ and the heat ${\displaystyle {(\Delta Q)}_r}$, change in internal energy ${\displaystyle (\Delta U)}$, and work done ${\displaystyle {(\Delta W)}_r,r=1,2,3}$ respectively. The temperature at ${\displaystyle A,B,C}$ are ${\displaystyle T_1=300K,T_2=600K}$ and ${\displaystyle T_3=455K}$. Indicate the pressure and volume at ${\displaystyle A,B}$ and${\displaystyle C}$ by ${\displaystyle P_r}$ and ${\displaystyle V_r,r=1,2,3,}$ respectively. Assume that intially pressure ${\displaystyle P_1=1.00atm.}$
Which of the following represents the correct values for the quantities indicated ?

Options

A. `V_(1)=3 xx 10^(-3)Rm^(3), P_(2)=0.5 atm`
B. `V_(2)=3 xx 10^(-3)Rm^(3), P_(3)=1.0 atm`
C. `V_(3)=3 xx 10^(-3)Rm^(3), P_(2)=2.0 atm`
D. `V_(2)=3 xx 10^(-3)Rm^(3), P_(3)=2.0 atm`

Answer

B

Explanation

To solve the problem step by step, we will analyze the reversible heat engine cycle involving an ideal monatomic gas. We will find the pressure and volume at points A, B, and C, given the temperatures and the initial pressure at point A.

Step 1: Identify the Given Values
- Temperature at point A, \( T_1 = 300 \, K \)
- Temperature at point B, \( T_2 = 600 \, K \)
- Temperature at point C, \( T_3 = 455 \, K \)
- Initial pressure at point A, \( P_1 = 1.00 \, atm \)
- The gas is monatomic and behaves ideally.

Step 2: Use the Ideal Gas Law
The ideal gas law is given by:
\( PV = nRT \)
where \( n \) is the number of moles, \( R \) is the ideal gas constant, and \( T \) is the temperature in Kelvin.

Since we have 1 mole of gas, we can express the pressure and volume at each point using the ideal gas law.

Step 3: Calculate Pressure at Point B
The process from A to B is isochoric (constant volume), and we can relate the pressures and temperatures at points A and B using the ratio:
\( \frac{P_1}{P_2} = \frac{T_1}{T_2} \)
Substituting the known values:
\( \frac{1 \, atm}{P_2} = \frac{300 \, K}{600 \, K} \)
Cross-multiplying gives:
\( P_2 = 2 \, atm \)

Step 4: Calculate Pressure at Point C
For the adiabatic process from B to C, we can use the relation for adiabatic processes for an ideal gas:
\( \frac{T_B}{T_C} = \left(\frac{P_B}{P_C}\right)^{\frac{\gamma - 1}{\gamma}} \)
For a monatomic gas, \( \gamma = \frac{5}{3} \). Rearranging gives:
\( P_C = P_B \left(\frac{T_C}{T_B}\right)^{\frac{\gamma}{\gamma - 1}} \)
Substituting the known values:
\( P_C = 2 \, atm \left(\frac{455 \, K}{600 \, K}\right)^{\frac{5/3}{2/3}} = 2 \, atm \left(\frac{455}{600}\right)^{\frac{5}{2}} \)
Calculating this gives:
\( P_C \approx 1.5 \, atm \)

Step 5: Calculate Volumes at Each Point
Using the ideal gas law, we can find the volumes at each point:
- At point A:
\( V_A = \frac{nRT_1}{P_1} = \frac{1 \cdot 0.0821 \cdot 300}{1} \approx 24.63 \, L \)
- At point B:
\( V_B = \frac{nRT_2}{P_2} = \frac{1 \cdot 0.0821 \cdot 600}{2} \approx 24.63 \, L \)
- At point C:
\( V_C = \frac{nRT_3}{P_C} = \frac{1 \cdot 0.0821 \cdot 455}{1.5} \approx 24.63 \, L \)

Summary of Results
- \( P_A = 1 \, atm \)
- \( P_B = 2 \, atm \)
- \( P_C \approx 1.5 \, atm \)
- \( V_A \approx 24.63 \, L \)
- \( V_B \approx 24.63 \, L \)
- \( V_C \approx 24.63 \, L \)

Conclusion
The correct values for the quantities indicated are:
- \( P_1 = 1 \, atm \)
- \( P_2 = 2 \, atm \)
- \( P_3 \approx 1.5 \, atm \)
- Volumes remain approximately constant due to the nature of the processes.