A gas expands in a piston-cylinder device from volume V1 to V2, the process being described by P=a/V+b, a and b are constants. Find the work done in the process.
To find the work done during the expansion of a gas in a piston-cylinder device, we start with the given pressure-volume relationship and apply the formula for work done in a thermodynamic process.
1. Identify the Work Done Formula:
The work done W during a gas expansion is given by the integral of pressure P with respect to volume V:
W=∫V2V1PdV
2. Substitute the Pressure Equation:
We are given that the pressure P is described by the equation:
P=aV+b
Therefore, we can substitute this expression into the work done formula:
W=∫V2V1(aV+b)dV
3. Separate the Integral:
We can break the integral into two parts:
W=∫V2V1aVdV+∫V2V1bdV
4. Evaluate the First Integral:
The first integral ∫aVdV evaluates to:
alnV∣∣∣V2V1=a(lnV2−lnV1)=aln(V2V1)
5. Evaluate the Second Integral:
The second integral ∫bdV evaluates to:
bV∣∣∣V2V1=b(V2−V1)
6. Combine the Results:
Now, we can combine the results from both integrals:
W=aln(V2V1)+b(V2−V1)
7. Final Expression for Work Done:
Thus, the work done during the gas expansion is:
W=aln(V2V1)+b(V2−V1)
The work done W during a gas expansion is given by the integral of pressure P with respect to volume V:
W=∫V2V1PdV
We are given that the pressure P is described by the equation:
P=aV+b
Therefore, we can substitute this expression into the work done formula:
W=∫V2V1(aV+b)dV
We can break the integral into two parts:
W=∫V2V1aVdV+∫V2V1bdV
The first integral ∫aVdV evaluates to:
alnV∣∣∣V2V1=a(lnV2−lnV1)=aln(V2V1)
The second integral ∫bdV evaluates to:
bV∣∣∣V2V1=b(V2−V1)
Now, we can combine the results from both integrals:
W=aln(V2V1)+b(V2−V1)
Thus, the work done during the gas expansion is:
W=aln(V2V1)+b(V2−V1)
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Single Correct
Explore 140 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Multiple Corrects
Explore 29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Exercise 2.2
Explore 28 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
Similar Questions
A sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
The work of expansion in adiabatic process (wadi) is related to work of expansion in isothermal process (wiso) is
View SolutionTemperature of two moles of an ideal gas is increased by 300K in a process V=aT, where a is positive constant. Find work done by the gas in the given process.
View Solution
Knowledge Check
A gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gas in these three processes then
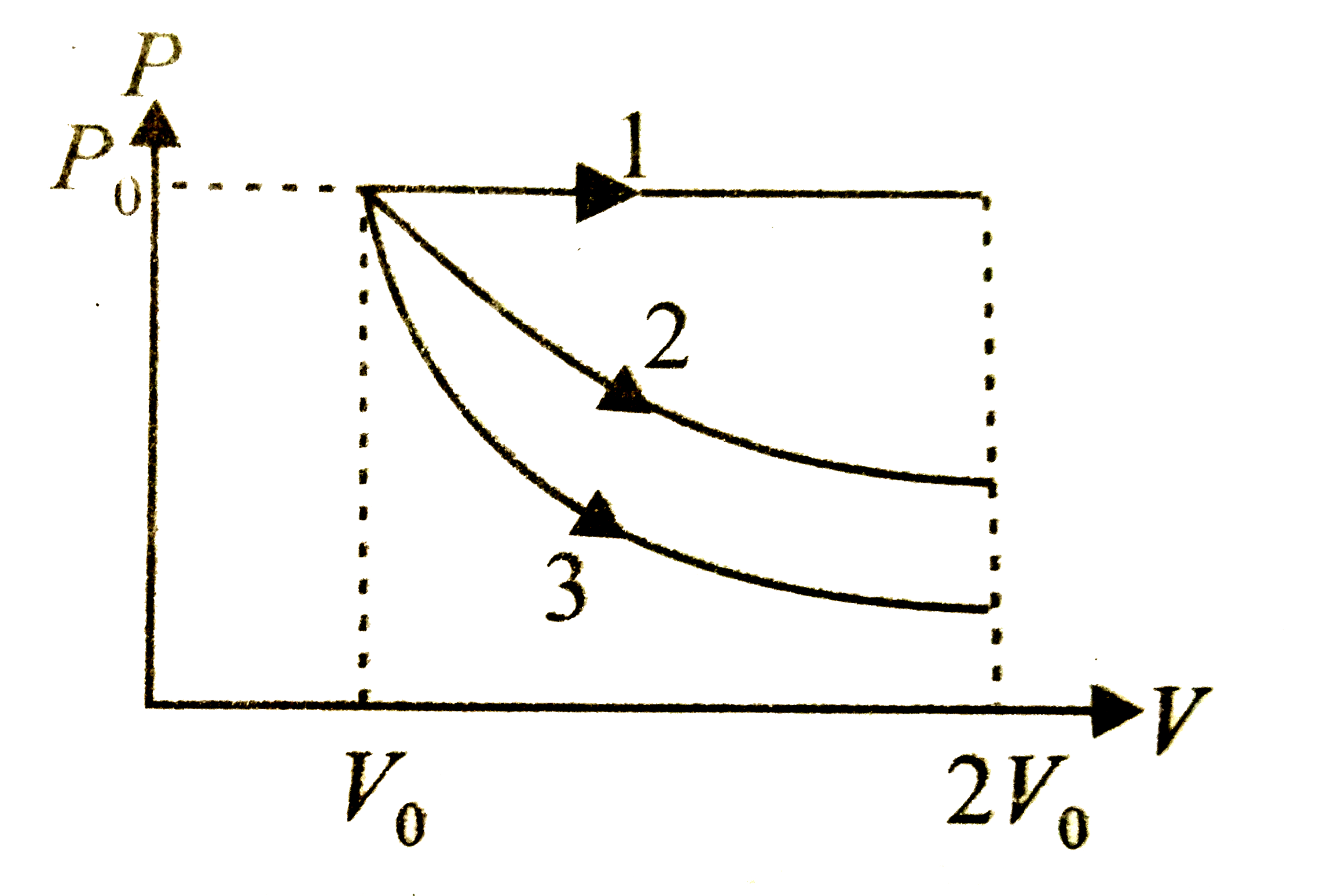 AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3
AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3
Pressure and volume of a gas changes from (p0V0) to (p04,2V0) in a process pV2= constant. Find work done by the gas in the given process.
View SolutionAt 27∘C two moles of an ideal monatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate
(a) final temperature of the gas
(b) change in its internal energy and
(c) the work done by the gas during the process. [ R=8.31J/mol−K]
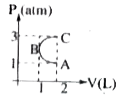
View SolutionIn the P-V diagram shown in figure ABC is a semicircle. The work done in the process A→B→C
View SolutionA sample of gas expands from volume V1 to V2. The amount of work done by the gas is greatest when the expansion is
View SolutionA gas is expanded from volume V1 to V2 through three different process:
a. Reversible adiabatic
b. Reversible isothermal
c. Irreversible adiabatic (against a constant external pressure Pex)
The correct option is
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
View SolutionIf a gas of a volume V1 at pressure p1 is compressed adiabatically to volume V2 and pressure p2, calculate the work done by the gas.
View Solution
