Gaseous hydrogen contained initially under standard conditions in sealed vessel of volume V=5L was cooled by ΔT=55K. Find how much the internal energy of the gas will change and what amount of heat will be lost by the gas.
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We need to find the change in internal energy (ΔU) and the amount of heat lost (ΔQ) by a sealed vessel of gaseous hydrogen when it is cooled by ΔT = 55 K.
Step 2: Identify Key Concepts
Since the vessel is sealed, the volume (V) remains constant. Therefore, the work done (W) is zero. According to the first law of thermodynamics:
ΔQ=ΔU+W
Since W=0, we have:
ΔQ=ΔU
Step 3: Use the Formula for Change in Internal Energy
The change in internal energy for an ideal gas can be expressed as:
ΔU=nCvΔT
Where:
- n = number of moles of the gas
- Cv = molar heat capacity at constant volume
- ΔT = change in temperature
Step 4: Calculate Molar Heat Capacity (C_v)
For a diatomic gas like hydrogen (H₂), the molar heat capacity at constant volume is given by:
Cv=Rγ−1
Where:
- R = universal gas constant =8.314J/(mol⋅K)
- γ = ratio of specific heats =1.4 for diatomic gases.
Step 5: Determine the Number of Moles (n)
Using the ideal gas law:
PV=nRT
At standard conditions (STP), the pressure P0=1.013×105Pa, volume V=5L=5×10−3m3, and standard temperature T0=273K.
Rearranging gives:
n=P0VRT0
Step 6: Substitute Values
Now substituting the values:
n=(1.013×105)×(5×10−3)(8.314)×(273)
Step 7: Calculate ΔU
Now we can substitute n, Cv, and ΔT into the equation for ΔU:
ΔU=nCvΔT
Step 8: Calculate ΔQ
Since ΔQ=ΔU, we can find the heat lost by the gas.
Step 9: Final Calculation
Putting all the values together, we can calculate ΔU and ΔQ.
Final Results
After performing the calculations, we find:
ΔU=ΔQ=−255J
We need to find the change in internal energy (ΔU) and the amount of heat lost (ΔQ) by a sealed vessel of gaseous hydrogen when it is cooled by ΔT = 55 K.
Since the vessel is sealed, the volume (V) remains constant. Therefore, the work done (W) is zero. According to the first law of thermodynamics:
ΔQ=ΔU+W
Since W=0, we have:
ΔQ=ΔU
The change in internal energy for an ideal gas can be expressed as:
ΔU=nCvΔT
Where:
- n = number of moles of the gas
- Cv = molar heat capacity at constant volume
- ΔT = change in temperature
For a diatomic gas like hydrogen (H₂), the molar heat capacity at constant volume is given by:
Cv=Rγ−1
Where:
- R = universal gas constant =8.314J/(mol⋅K)
- γ = ratio of specific heats =1.4 for diatomic gases.
Using the ideal gas law:
PV=nRT
At standard conditions (STP), the pressure P0=1.013×105Pa, volume V=5L=5×10−3m3, and standard temperature T0=273K.
n=P0VRT0
Now substituting the values:
n=(1.013×105)×(5×10−3)(8.314)×(273)
Now we can substitute n, Cv, and ΔT into the equation for ΔU:
ΔU=nCvΔT
Since ΔQ=ΔU, we can find the heat lost by the gas.
Putting all the values together, we can calculate ΔU and ΔQ.
After performing the calculations, we find:
ΔU=ΔQ=−255J
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Solved Examples
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.1
20 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
A gas consisting of rigid diatomic molecules (degrees of freedom r = 5) under standard conditions (P0=105 Pa and T0=273K) was compressed adiabatically η=5 times. Find the mean kinetic energy of a rotating molecule in the final state.
View SolutionA cylinder contains 3 moles of oxygen at a temperature of 27∘C. The cylinder is provided with a frictionless piston which maintains a constant pressure of 1 atm on the gas. The gas is heated until its temperature rises to 127∘C.
a. How much work is done by the gas in the process ?
b. What is the change in the internal energy of the gas ?
c. How much heat was supplied to the gas ?
For oxygen CP=7.03calmol−1.∘C−1.
View Solution
Knowledge Check
A gas is allowed to expand in a well insulated container against a constant external pressure of 2.5 atm from an initial volume of 2.50 L to a final volume of 4.50 L. The change in internal energy ΔU of the gas in joules will be
A1136.25 JB−500JC-505 JD+505 J
A gas is allowed to expand in a well insulated container against a constant external pressure of 2.5atm from an initial volume of 2.50L to a final volume of 4.50L. The change in internal energy ΔU of the gas in joules will be:
View SolutionA gas consisting of rigid di-atomic molecules (degree of freedom =5) at pressure p0=105N/m2 and temperature 273K was compressed adiabatically 5 times. The mean kinetic energy of rotating molecules in final state is nx10−21J. Find value of 'n'.(K=1.38×10−23,(5)2/5=1.90).
View SolutionCp is always greater than Cv for a gas, which of the following statements provide, partly or wholly, the reason for this?
(i) No work is done by a gas at constant volume
(ii) When a gas absorbs heat at constant pressure, its volume must change
(iii) For the same change in temperature, the internal energy of a gas changes by a smaller amount at constant volume that at constant pressure
(iv) The internal energy of an ideal gas is a function only of its temperature
View SolutionAn ideal gas is taken round a cyclic thermodynamic process ABCA as shown if Fig. If the internal energy of the gas at point A is assumed zero while at B it is 50 J. The heat absorbed by the gas in the process BC is 90 J.
(a) What is the internal energy og the gas at point C ?
(b) How much heat energy is absorbed by the gas in the process AB?
(c ) Find the heat energy rejected or absorbed by the gas in the process CA.
(d) What is the net work done by the gas in the complete cycle ABCA ?
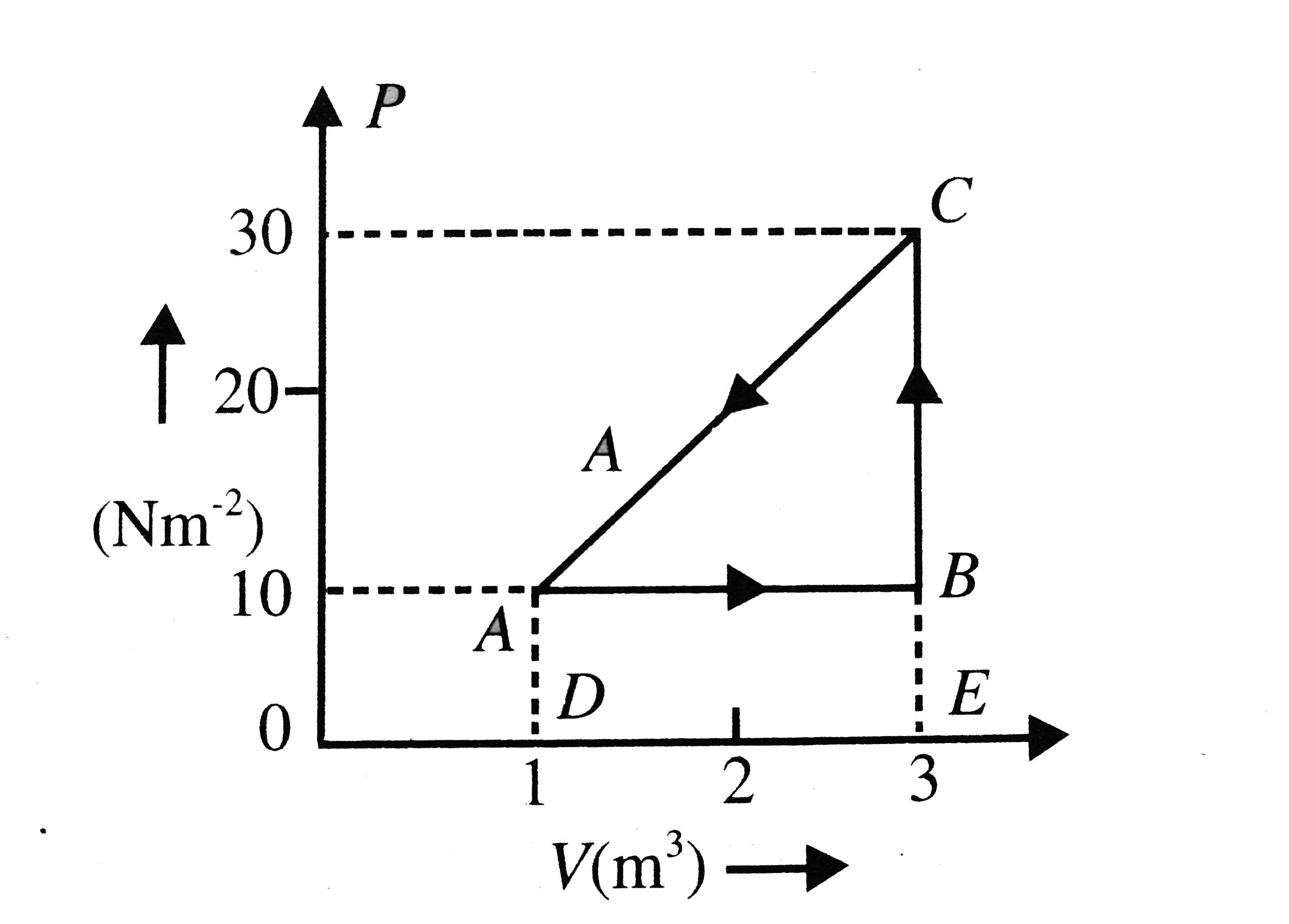
View SolutionSix grams of hydrogen gas at a temperature of 273 K isothoermally expanded to five times its initial volume and then isochorically heated so that the pressure in the final state becomes equal to that in the initial state. Find the total amount of heat absorbed by the gas during the entire process.
View SolutionA gas expands in an insulated container against a constant external pressure of 1.5 atm from an initial volume of 1.2 L to 4.2 L. The change in internal energy (ΔU) of gas is nearly (1 L-atm = 101.3 J)
View SolutionThere are two vessels. Each of them contains one moles of a monoatomic ideal gas. Initial volume of the gas in each vessel is 8.3×10−3m3at27∘C. Equal amount of heat is supplied to each vessel. In one of the vessels, the volume of the gas is doubled without change in its internal energy, whereas the volume of the gas is held constant in the second vessel. The vessels are now connected to allow free mixing of the gas. Find the final temperature and pressure of the combined gas system.
View Solution
