The ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
the length of the rod
the diameter of the rod
the cross sectional area of the rod
the temperature difference (θ2−θ1) between the ends of the rod
The correct Answer is:C, D
To solve the problem, we need to analyze the relationship between the rate of heat flow along a metal rod and various factors such as temperature difference, length of the rod, and cross-sectional area.
1. Understanding Heat Flow:
Heat flows from a region of higher temperature to a region of lower temperature. In this case, the ends of the rod are at temperatures θ2 and θ1 with θ2>θ1.
2. Using Fourier's Law of Heat Conduction:
According to Fourier's law, the rate of heat flow QT (where Q is the heat transferred and T is the time) is given by the formula:
QT=k⋅A⋅θ2−θ1L
where:
- k is the thermal conductivity of the material,
- A is the cross-sectional area of the rod,
- θ2−θ1 is the temperature difference,
- L is the length of the rod.
3. Identifying Proportional Relationships:
- From the equation, we can see that the rate of heat flow QT is directly proportional to:
- The temperature difference θ2−θ1 (Option 4).
- The cross-sectional area A of the rod (Option 3).
- The rate of heat flow is inversely proportional to the length L of the rod (Option 1), meaning that as the length increases, the rate of heat flow decreases.
4. Analyzing the Options:
- Option 1: Length of the rod - Incorrect (inversely proportional).
- Option 2: Diameter of the rod - Incorrect (directly proportional to the area, not diameter).
- Option 3: Cross-sectional area of the rod - Correct (directly proportional).
- Option 4: Temperature difference θ2−θ1 - Correct (directly proportional).
5. Conclusion:
The rate of flow of heat along the rod is directly proportional to the cross-sectional area of the rod and the temperature difference between the ends of the rod. Therefore, the correct answers are Option 3 and Option 4.
Heat flows from a region of higher temperature to a region of lower temperature. In this case, the ends of the rod are at temperatures θ2 and θ1 with θ2>θ1.
According to Fourier's law, the rate of heat flow QT (where Q is the heat transferred and T is the time) is given by the formula:
QT=k⋅A⋅θ2−θ1L
where:
- k is the thermal conductivity of the material,
- A is the cross-sectional area of the rod,
- θ2−θ1 is the temperature difference,
- L is the length of the rod.
- From the equation, we can see that the rate of heat flow QT is directly proportional to:
- The temperature difference θ2−θ1 (Option 4).
- The cross-sectional area A of the rod (Option 3).
- The rate of heat flow is inversely proportional to the length L of the rod (Option 1), meaning that as the length increases, the rate of heat flow decreases.
- Option 1: Length of the rod - Incorrect (inversely proportional).
- Option 2: Diameter of the rod - Incorrect (directly proportional to the area, not diameter).
- Option 3: Cross-sectional area of the rod - Correct (directly proportional).
- Option 4: Temperature difference θ2−θ1 - Correct (directly proportional).
The rate of flow of heat along the rod is directly proportional to the cross-sectional area of the rod and the temperature difference between the ends of the rod. Therefore, the correct answers are Option 3 and Option 4.
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Integer
8 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Single Correct
148 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A body cools in a surrounding of constant temperature 30∘C Its heat capacity is 2J/∘C. Initial temperature of cooling is valid. The body of mass 1 kg cools to 38∘C in 10 min
When the body temperature has reached 38∘C, it is heated again so that it reaches 40∘C in 10 min. The heat required from a heater by the body is
View Solution2 kg of ice at −15∘C is mixed with 2.5 kg of water at 25∘C in an insulating container. If the specific heat capacities of ice and water are 0.5cal/g∘C and 1cal/g∘C, find the amount of water present in the container? (in kg nearest integer)
View SolutionThe design of some physical instrument requires that there be a constant difference in length of 10 cm between an iron rod and a copper cylinder laid side by side at all temperature find their lengths
(αFe=11×106.∘C−1,αCu=17×10−6.∘C−1)
View SolutionThe displacement of a particle is given by y=(6t2+3t+4)m, where t is in seconds. Calculate the instantaneous speed of the particle.
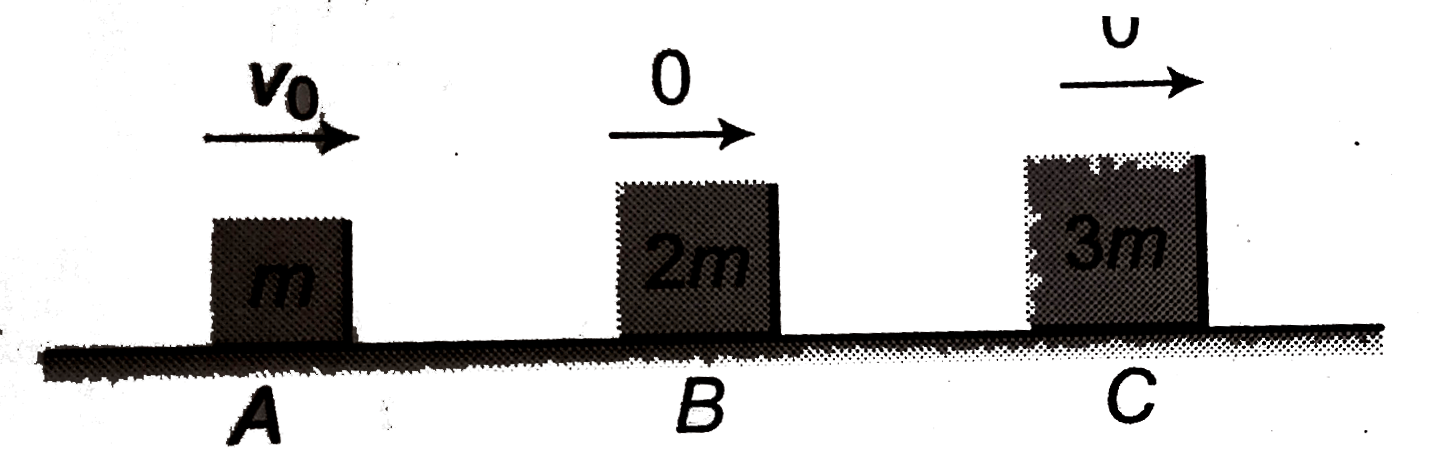
View SolutionThree objects A ,B and C are kept in a straight line on a smooth horizontal surface. These have masses m, 2m and 3m , respectively . The head - on elastic collision takes place between A and B and then B makes completely inelastic collision with C. All motions occur on the same straight line. The final speed of C will be
View SolutionOne end of a metal rod is kept in a furnce. In steady state, the temperature of the rod
View SolutionThe ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
View SolutionThe two ends of a metal rod are maintained at temperatures 100∘C and 110∘C . The rate of heat flow in the rod is found to be 4.0j/s. If the ends are maintaind at temperatures 200∘C and 210∘C, the rate of heat flow will be :
View SolutionIf the end of metal rod is heated then the rate of flow the heat does not depend on
View SolutionThe ends of a metal rod are kept at temperature theta_(1) and theta_(2) with theta_(2) gt theta_(1) . At steady state the rate of flow of heat along the rod is directly proportional to
View Solutionकिसी धातु की छड़ के दो सिरों के तापों को क्रमशः 100∘C तथा 110∘C पर रखा जाता है जिससे छड़ में ऊष्मा का प्रवाह 4.0 जूल/से पाया जाता है।यदि इन सिरों के तापों को क्रमशः 200∘C तथा 210∘C पर रखा जाये तो ऊष्मा प्रवाह होगा:
View SolutionWhich of the following cylindrical rods of the same metal has the highest rate of flow of heat ? The rods have equal difference of temperature between their ends :
View SolutionThe two ends of a metal rod are maintained at temperatures 100^(@)C and 110^(@)C . The rate of heat flow in the rod is found to be 4.0" Js"^(-1) . If the ends are maintained at temperatures 200^(@)C and 210^(@)C , the rate of heat flow will be :
View SolutionOne end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
View SolutionAmount of heat conducted through a metal rod is directly proportional to
View Solution
