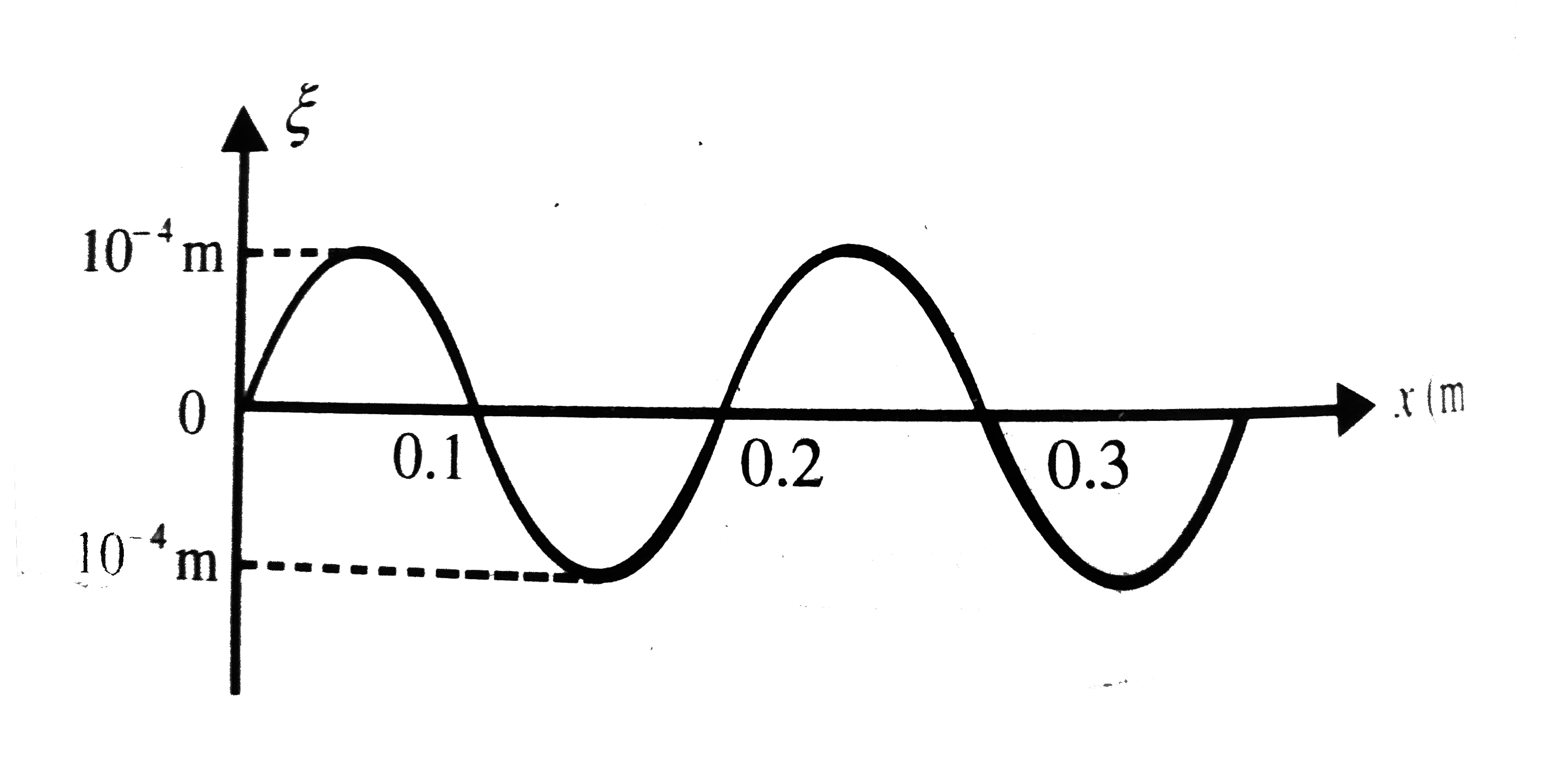
For a sound wave travelling towards +x direction, sinusoidal longitudinal displacement ε at a certain time is given as a function of x (Fig). If bulk modulus of air is B=5×105Nm2, the variation of pressure excess will be
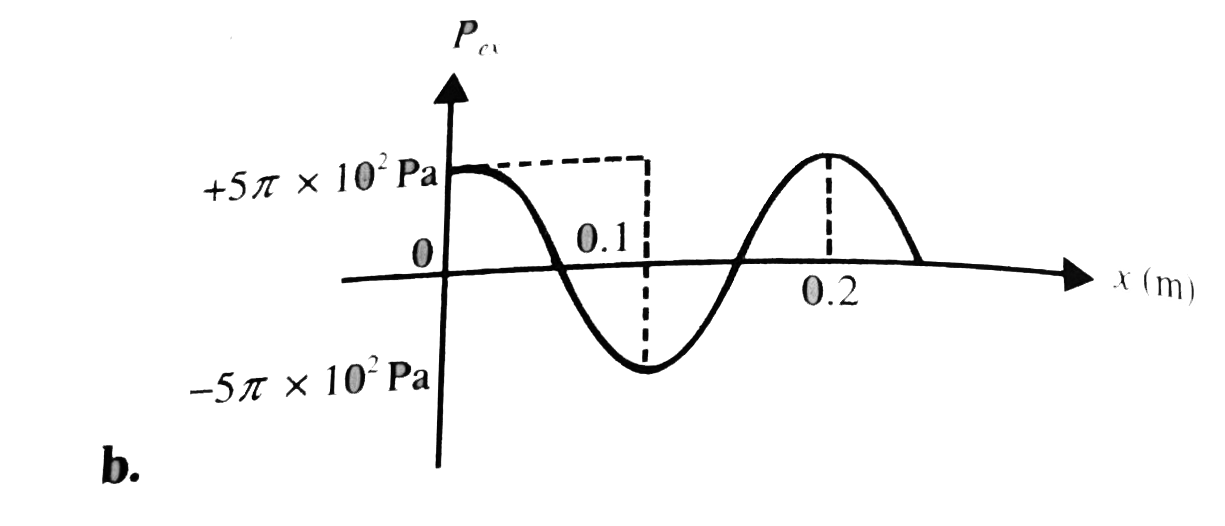
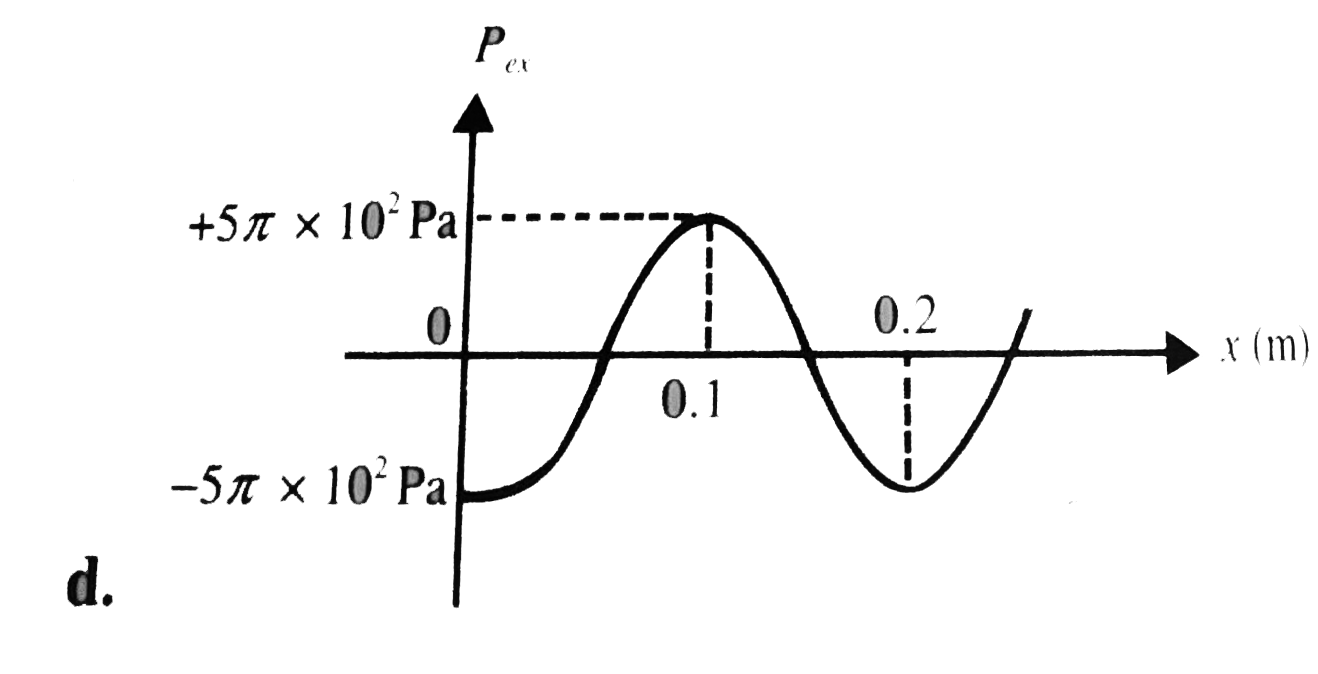
The correct Answer is:A
ε=Asin(kx−ωt)
Pex=−Bdεdx=−Bakcos(kx−ωt)
Amplitude of Pex is
Bak=(5×105)(10−4)(2π0.2)
=5π×102Pa
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Multiple Correct44videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning24videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective56videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type5videos
SUPERPOSITION AND STANDING WAVES
Similar Questions
The equation of displacement due to a sound wave is s=s0sin^(2)((wt-kx)). if the bulk modulus of the medium is B, then the equation of pressure variation due to that sound is
View SolutionA sound wave of wavelength 20π cm travels in air if the difference between the maximum and minimum pressures at a given point is 3.0×10−3N/m2.
Now sound level is increased by 20 dB, if the new amplitude of vibration of the particles of the medium at that given point is 20k (in Å) then 'k' is : (The bulk modulus of air is 1.5×105N/m2) (wavelength is same in both cases )View SolutionA person sitting at a distance of 10m from a point source of sound of power W0 writes down the following equation for the waves received by him.
y=Asin(20πx+7000πt)
(a) Determine the density of the air, if the Bulk modules of air =1.40×105Nm−2
(b) If the largest pressure amplitude tolerable to a human car is 28Pa then determine the maximum power W0 of the second source and the displacement amplitude A of the waves receive by him.View SolutionCalculate the speed of longitudinal sound wave in a liquid. The bulk modulus for the liquid is 20×109N/m2 and its density is 9.5×103kg/m3.
View SolutionThe equation of a sound wave in air is given by △p=(0.02)sin[(3000)t−(9.0)x], where all variables are is SI units. (a) find the frequency, wavelength and the speed of sound wave in air. (b) If the equilibrium pressure of air is 1.01×105Nm2, What are the maximum and minimum pressure at a point as the wave passes through that point?
View SolutionThe increase in pressure required to decrease volume by 0.005% of150litre liquid (in kPa) is (Bulk modulus of liquid, B=3x109Nm2)
View SolutionA sound wave of wavelength 40 cm travels in air. If the difference between the maximum and minimum pressures at a given point is 1.0×10−3Nm−2, find the amplitude of vibration of the particle o the medium. The bulk modulus of air is 1.4×105Nm−2.
View SolutionThe density of aluminium is 2.7×103kg/m3 and its Young's modulus is 7.0×1010N/m2. Calculate the velocity of sound wave in the bar.
View SolutionA plane longitudinal wave having angular frequency ω = 500 rad /sec is travelling in positive x-direction in a medium of density ρ =1 kg/m and bulk modulus 4×104N/m2 . The loudness at a point in the medium is observed to be 20 dB. Assuming at x = 0 initial phase of the medium particles to be zero, find the equation of the wave
View SolutionA longitudinal sine wave is travelling in air along positive x-direction. Displacement(s) of particles from their mean positions at a particular time t are shown in the figure. Choose the correct options for that instant only
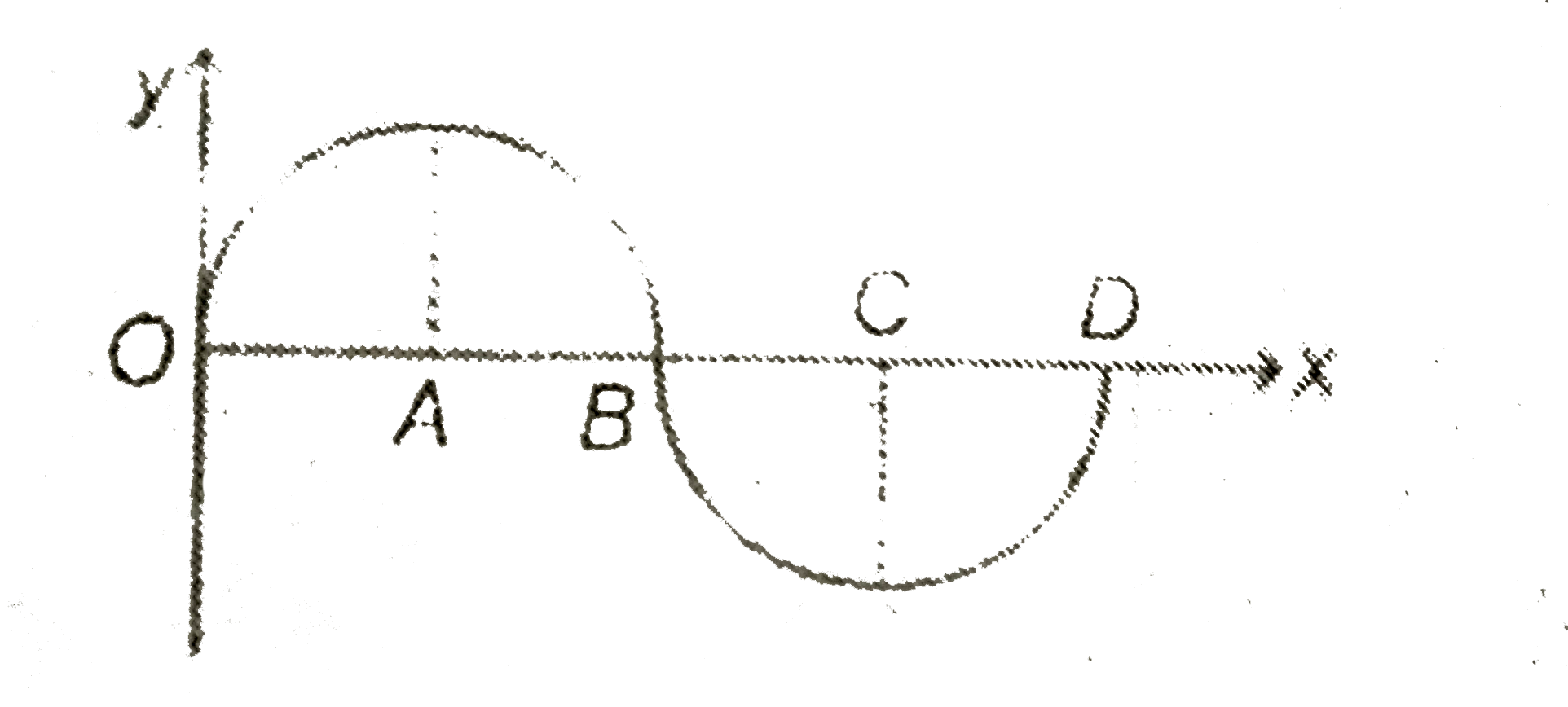
View Solution