A stationary observer receives sound waves from two tuning forks, one of which approaches and the other recedes with the same velocity. As this takes place, the observer hears beats of frequency υ=2Hz. Find the velocity of each tuning fork if their oscillation frequency is υ0=680Hz and the velocity of sound in air is υs=340ms.
To solve the problem, we will use the concept of beats and the Doppler effect. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Problem
We have two tuning forks, one approaching the observer and the other receding from the observer. The observer hears beats, which is the difference in frequency between the two sound waves. The beat frequency is given as ν=2Hz, and the natural frequency of the tuning forks is ν0=680Hz.
Step 2: Apply the Doppler Effect
The apparent frequency heard by the observer when the tuning fork is approaching is given by:
f1=vsvs−vν0
where vs is the speed of sound in air (340 m/s) and v is the speed of the tuning fork.
When the tuning fork is receding, the apparent frequency is:
f2=vsvs+vν0
Step 3: Set Up the Beat Frequency Equation
The beat frequency is the absolute difference between the two frequencies:
ν=|f1−f2|
Substituting the expressions for f1 and f2:
ν=∣∣∣vsvs−vν0−vsvs+vν0∣∣∣
Step 4: Simplify the Expression
Factoring out ν0:
ν=ν0∣∣∣vsvs−v−vsvs+v∣∣∣
Finding a common denominator:
ν=ν0∣∣∣vs(vs+v)−vs(vs−v)(vs−v)(vs+v)∣∣∣
This simplifies to:
ν=ν0∣∣∣vs⋅2v(vs−v)(vs+v)∣∣∣
Step 5: Substitute Known Values
We know ν=2Hz and ν0=680Hz:
2=680⋅∣∣∣2v(340−v)(340+v)∣∣∣
This simplifies to:
2680=∣∣∣2v(340−v)(340+v)∣∣∣
1340=2v(340−v)(340+v)
Step 6: Cross-Multiply and Rearrange
Cross-multiplying gives:
(340−v)(340+v)=680v
Expanding the left-hand side:
3402−v2=680v
Rearranging gives us a quadratic equation:
v2+680v−3402=0
Step 7: Solve the Quadratic Equation
Using the quadratic formula v=−b±√b2−4ac2a:
Here, a=1,b=680,c=−3402:
v=−680±√6802+4⋅34022
Calculating the discriminant:
6802+4⋅3402=462400+462400=924800
v=−680±9602
Calculating the two possible values:
1. v=2802=140m/s (valid)
2. v=−16402=−820m/s (not valid)
Step 8: Final Answer
The velocity of each tuning fork is v=140m/s.
---
We have two tuning forks, one approaching the observer and the other receding from the observer. The observer hears beats, which is the difference in frequency between the two sound waves. The beat frequency is given as ν=2Hz, and the natural frequency of the tuning forks is ν0=680Hz.
The apparent frequency heard by the observer when the tuning fork is approaching is given by:
f1=vsvs−vν0
where vs is the speed of sound in air (340 m/s) and v is the speed of the tuning fork.
f2=vsvs+vν0
The beat frequency is the absolute difference between the two frequencies:
ν=|f1−f2|
Substituting the expressions for f1 and f2:
ν=∣∣∣vsvs−vν0−vsvs+vν0∣∣∣
Factoring out ν0:
ν=ν0∣∣∣vsvs−v−vsvs+v∣∣∣
Finding a common denominator:
ν=ν0∣∣∣vs(vs+v)−vs(vs−v)(vs−v)(vs+v)∣∣∣
This simplifies to:
ν=ν0∣∣∣vs⋅2v(vs−v)(vs+v)∣∣∣
We know ν=2Hz and ν0=680Hz:
2=680⋅∣∣∣2v(340−v)(340+v)∣∣∣
This simplifies to:
2680=∣∣∣2v(340−v)(340+v)∣∣∣
1340=2v(340−v)(340+v)
Cross-multiplying gives:
(340−v)(340+v)=680v
Expanding the left-hand side:
3402−v2=680v
Rearranging gives us a quadratic equation:
v2+680v−3402=0
Using the quadratic formula v=−b±√b2−4ac2a:
Here, a=1,b=680,c=−3402:
v=−680±√6802+4⋅34022
Calculating the discriminant:
6802+4⋅3402=462400+462400=924800
v=−680±9602
Calculating the two possible values:
1. v=2802=140m/s (valid)
2. v=−16402=−820m/s (not valid)
The velocity of each tuning fork is v=140m/s.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective
56 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Single Correct
252 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.1
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
A stationary observer receives sonic oscillations from two tuning forks one of which approaches and the other recedes with the same velocity. As this takes place, the observer hears the beats of frequency f=2.0HZ. Find the velocity of each tuning fork if their oscillation frequency is fo=680HZ and the velocity of sound in air is υ=340m/s.
View SolutionA stationary observer receives sound from two identical tuning forks, one of which approaches and the other one recedes with the same speed (much less than the speed of sound). The observer hears 2 beats/ sec. The oscillation frequency of each tuning fork is v0=1400 Hz and the velocity of sound in air is 350 m/s. The speed of each tuning fork is close to :
View Solution
Knowledge Check
A person is observing two trains, one is approaching him with a velocity of of 4 m/s while the other is receding from him with the same velocity. IF both the trains blow their respective whistles of frequency 240 hertz, the beat frequency heard by the observer will be (speed of sound in air = 320 m/s)
A6B3CzeroD12
Distance travelled by the sound produced by a tuning fork of frequency 50 Hz completing 200 vibrations is, (the velocity of sound in air is 330 m/s)
View SolutionTwo tuning forks with natural frequencies of 340Hz each move relative to a stationary observer. One fork moves away form the observer, while the other moves towards him at the same speed. The observer hears beats of frequency 3Hz. Find the speed of the tuning fork.
View SolutionTwo tuning forks with natural frequencies 340HZ each move relative to a stationary observer . One forks moves away from the oberver while the other moves towards him at the same speed . The observer hears beats of frequency 3HZ . Find the speed the of the tuning fork (velocity of sound in air is 340m/s) .
View Solution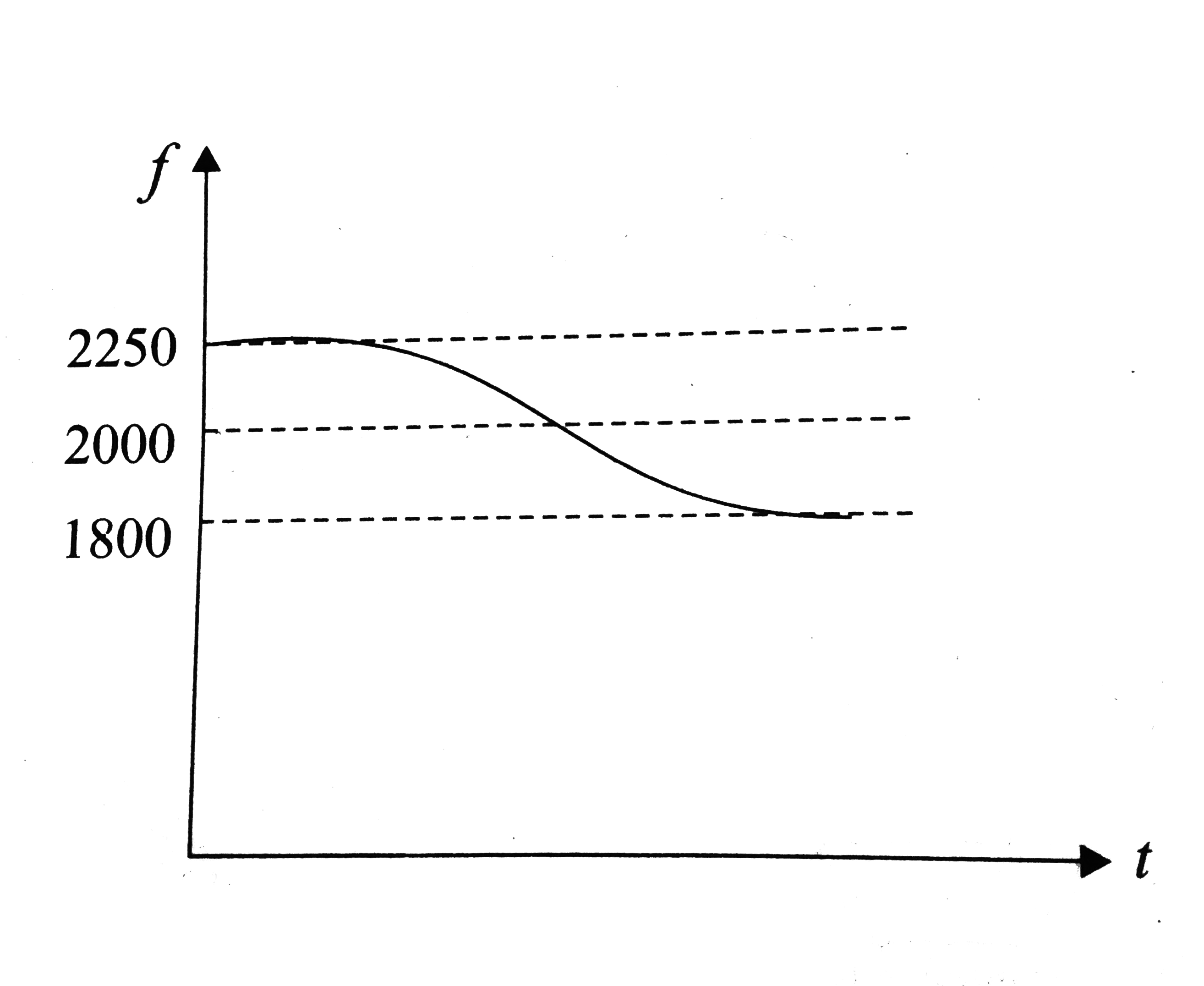
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionA standing tuning fork of frequency f is used to find the velocity of sound in air by resonance column appartus. The difference two resonating lengths is 1.0m. Then the velocity of sound in air is
View SolutionHow far does the sound travel in air when a tuning fork of frequency 500 Hz completes 25 vibrations ? Velocity of sound in air is 332 ms−1.
View SolutionAn engine blowing a whistle of frequency 133 Hz moves with a velocity of 60ms towards a hill from which an echo is heard. Calculate the frequency of the echo heard by the driver. (velocity of sound in air in 340ms.)
View Solution
