Two sources A and B are sounding notes of frequency 680 Hz. A listener moves from A to B with a constant velocity u. If the speed of sound is 340 m/s, What must be the value of u so that he hears 10 beats per second?
2.0ms
2.5ms
30ms
3.5ms
The correct Answer is:B
To solve the problem, we need to find the value of the listener's velocity u such that he hears 10 beats per second when moving from source A to source B, both emitting sound at a frequency of 680 Hz. The speed of sound in air is given as 340 m/s.
1. Identify the Frequencies:
- Both sources A and B emit a frequency f0=680Hz.
2. Determine the Apparent Frequencies:
- When the listener moves towards source B, the apparent frequency fB heard from source B is given by the formula:
fB=f0(v+uv)
where v is the speed of sound (340 m/s) and u is the listener's speed.
- When the listener moves away from source A, the apparent frequency fA heard from source A is given by:
fA=f0(v−uv)
3. Substituting Values:
- Substitute f0=680Hz and v=340m/s into the equations:
fB=680(340+u340)=680(1+u340)
fA=680(340−u340)=680(1−u340)
4. Calculate the Beat Frequency:
- The beat frequency Δf is given by:
Δf=fB−fA
- Substitute the expressions for fB and fA:
Δf=680(1+u340)−680(1−u340)
- Simplifying this gives:
Δf=680(u340+u340)=680(2u340)=4u
5. Set the Beat Frequency to 10 Hz:
- We know from the problem that the beat frequency is 10 Hz:
4u=10
6. Solve for u:
- Rearranging gives:
u=104=2.5m/s
Final Answer:
The value of u must be 2.5m/s.
---
- Both sources A and B emit a frequency f0=680Hz.
- When the listener moves towards source B, the apparent frequency fB heard from source B is given by the formula:
fB=f0(v+uv)
where v is the speed of sound (340 m/s) and u is the listener's speed.
fA=f0(v−uv)
- Substitute f0=680Hz and v=340m/s into the equations:
fB=680(340+u340)=680(1+u340)
fA=680(340−u340)=680(1−u340)
- The beat frequency Δf is given by:
Δf=fB−fA
- Substitute the expressions for fB and fA:
Δf=680(1+u340)−680(1−u340)
- Simplifying this gives:
Δf=680(u340+u340)=680(2u340)=4u
- We know from the problem that the beat frequency is 10 Hz:
4u=10
- Rearranging gives:
u=104=2.5m/s
The value of u must be 2.5m/s.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Multiple Correct
44 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning
24 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
Two sources A and B are sounding notes of frequency 660 Hz. A listener moves from A to B with a constant velocity u. If the speed is 330 m/s , what must be the value of u so that he hears 8 beats per second ?
View SolutionA and B are two identical sound sources cachemitting a note of frequency 1000 Hz. A person moves from A to B along the line joining the two sources. How fast should be move to that he has 7 beats per second. velocity of sound 330 m/s ?
View SolutionTwo sources of sound S1 and S2 produce sound waves of same frequency 660Hz. A listener is moving from source S1 towards S2 with a constant speed um/s and he hears 10 beats/s. The velocity of sound is 330m/s. Then, u equals :
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionThe frequency of the 5th harmonic of a pipe closed at one end is 680 Hz. If the speed of the sound is 340 m/s then the length of the pipe will be
View Solution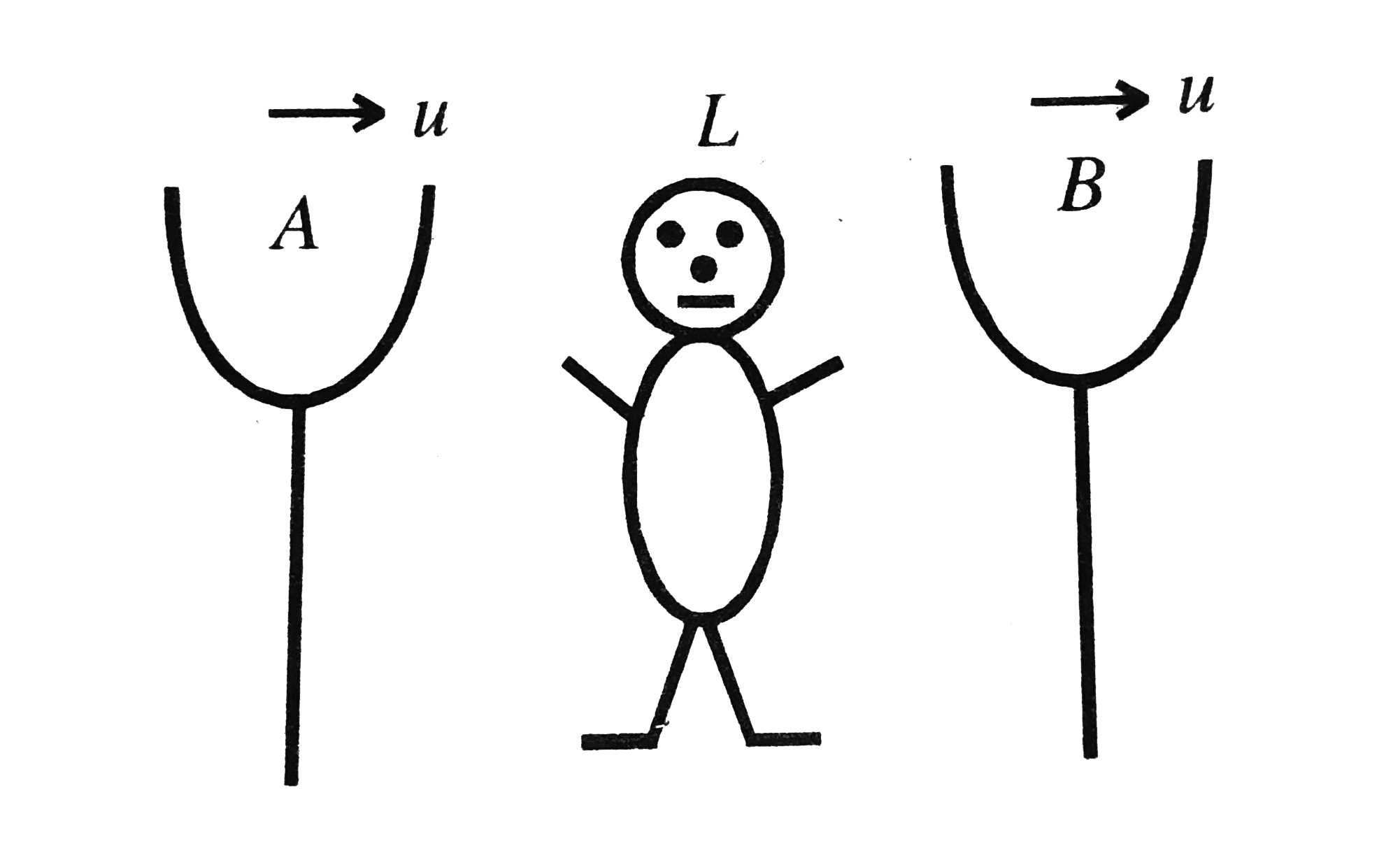
Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).
View Solution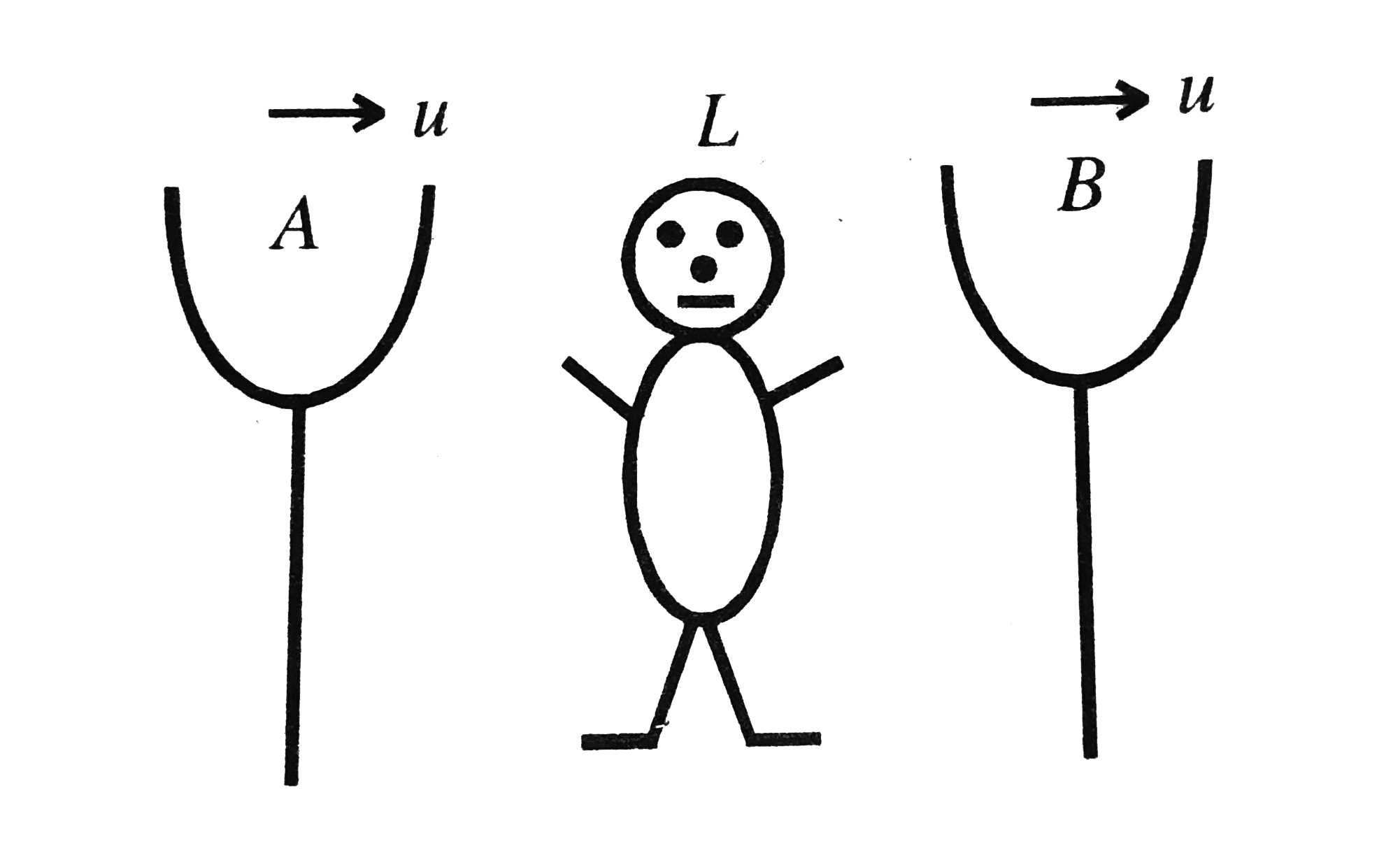- Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).
View Solution A source of sound emitting a note of frequency 200 Hz moves towards an observer with a velocity v equal to the velocity of sound. If the observer also moves away from the source with the same velocity v, the apparent frequency heard by the observer is
View SolutionTwo sources S1 and S2 of sound having frequencies 338Hz and 342Hz are separated by a large distance. The speed of sound is 340 ms^(-1). With what velocity should an observer move from source S2→S1 so that he hears no beats?
View SolutionA person with vibrating tuning fork of frequency 338 Hz is moving towards a vertical wall with speed of 2ms−1 Velocity of sound in air is 340ms−1 The number of beats heard per second is
View Solution