A and B are two identical sound sources cachemitting a note of frequency 1000 Hz. A person moves from A to B along the line joining the two sources. How fast should be move to that he has 7 beats per second. velocity of sound 330 m/s ?
The correct Answer is:1.15m/s
To solve the problem step by step, we will use the concept of the Doppler effect and the information provided in the question.
Step 1: Understand the Problem
We have two identical sound sources (A and B) emitting sound at a frequency of 1000 Hz. A person is moving from source A to source B and we need to find out how fast he should move to hear 7 beats per second.
Step 2: Define the Variables
- Frequency of the sound sources, f0=1000Hz
- Velocity of sound, v=330m/s
- Beats per second, Δf=7Hz
Step 3: Apply the Doppler Effect
The frequency heard by the observer moving towards source A and away from source B can be calculated using the Doppler effect formula.
For source A (moving towards):
fA=v+vovf0
For source B (moving away):
fB=v−vovf0
Step 4: Set Up the Equation for Beats
The difference in frequencies (beats) is given by:
|fA−fB|=7
This implies:
fA−fB=7
Step 5: Substitute the Frequencies
Substituting fA and fB into the beats equation:
(330+vo330⋅1000)−(330−vo330⋅1000)=7
Step 6: Simplify the Equation
This simplifies to:
(330+vo)⋅1000−(330−vo)⋅1000330=7
1000(330+vo−330+vo)330=7
2000vo330=7
Step 7: Solve for vo
Now, multiply both sides by 330:
2000vo=7⋅330
2000vo=2310
vo=23102000=1.155m/s
Step 8: Final Answer
The speed at which the person should move is approximately:
vo≈1.15m/s
We have two identical sound sources (A and B) emitting sound at a frequency of 1000 Hz. A person is moving from source A to source B and we need to find out how fast he should move to hear 7 beats per second.
- Frequency of the sound sources, f0=1000Hz
- Velocity of sound, v=330m/s
- Beats per second, Δf=7Hz
The frequency heard by the observer moving towards source A and away from source B can be calculated using the Doppler effect formula.
fA=v+vovf0
For source B (moving away):
fB=v−vovf0
The difference in frequencies (beats) is given by:
|fA−fB|=7
This implies:
fA−fB=7
Substituting fA and fB into the beats equation:
(330+vo330⋅1000)−(330−vo330⋅1000)=7
This simplifies to:
(330+vo)⋅1000−(330−vo)⋅1000330=7
1000(330+vo−330+vo)330=7
2000vo330=7
Now, multiply both sides by 330:
2000vo=7⋅330
2000vo=2310
vo=23102000=1.155m/s
The speed at which the person should move is approximately:
vo≈1.15m/s
Topper's Solved these Questions
Similar Questions
Two sources A and B are sounding notes of frequency 660 Hz. A listener moves from A to B with a constant velocity u. If the speed is 330 m/s , what must be the value of u so that he hears 8 beats per second ?
View SolutionTwo sources A and B are sounding notes of frequency 680 Hz. A listener moves from A to B with a constant velocity u. If the speed of sound is 340 m/s, What must be the value of u so that he hears 10 beats per second?
View SolutionTwo sound sources emitting sound each of wavelength λ are fixed at a given distance apart. A listener moves with a velocity u along the line joining the two sources. The number of beats heard by him per second is
View SolutionA sound source emitting sound of frequency 450 Hz is approaching a stationary observer with velocity 30ms−1 and another identical source is going away from the observer with the same velocity. If the velocity of sound is 330ms−1, then the difference of frequencies heard by observer is
View SolutionA stationary source emits sound waves of frequency 500 Hz. Two observes moving along a line passing through the source detect sount to be of frequencies 480 Hz and 530 Hz.Their respective speeds are, in ms−1
(Given speed of sound =300m/s)
View SolutionA man holding a sound source at the top of a tower emitting frequency of sound as v=1000Hz. Suddenly it slips from his hand and falls down with 'g' acceleration. The frequency of sound heard by the man at t=4sec. (Velocity of sound =320m/s, g=10m/s2)
View SolutionA stationary source of sound is emitting sound of frequency 500Hz. Two observers A and B lying on the same line as the source, observe frequencies 480Hz and 530Hz respectively. The velocity of A and B respectively are (in m/s), speed of sound =300m/s.
View SolutionTwo sources of sound S1 and S2 produce sound waves of same frequency 660Hz. A listener is moving from source S1 towards S2 with a constant speed um/s and he hears 10 beats/s. The velocity of sound is 330m/s. Then, u equals :
View SolutionA source of sound emitting a note of frequency 200 Hz moves towards an observer with a velocity v equal to the velocity of sound. If the observer also moves away from the source with the same velocity v, the apparent frequency heard by the observer is
View SolutionA source of sound of frequency 1000 Hzmoves to the right with a speed of 50 m/s relative to the ground. To its right is a reflecting surface moving to the left as shown in figure. Speed of the sound in air is 330 m/s.
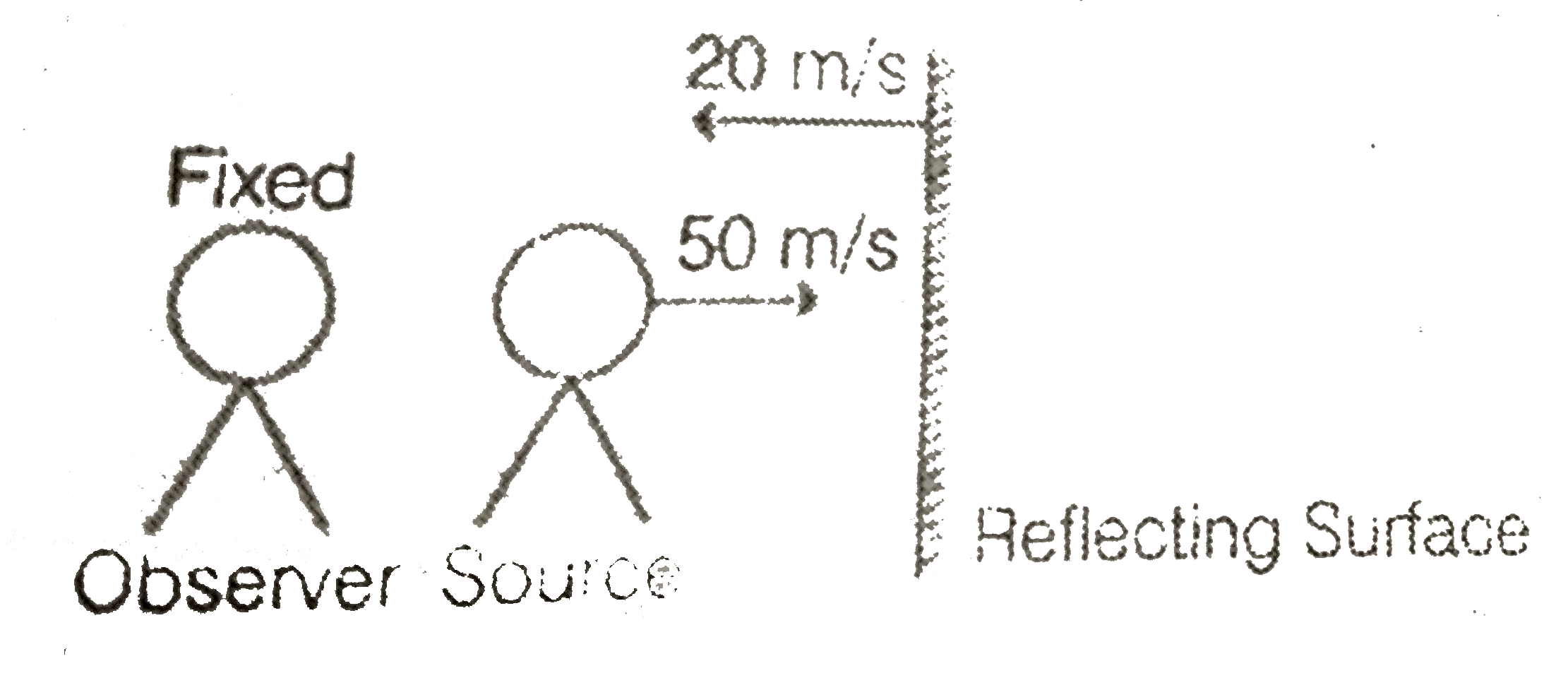

View Solution

