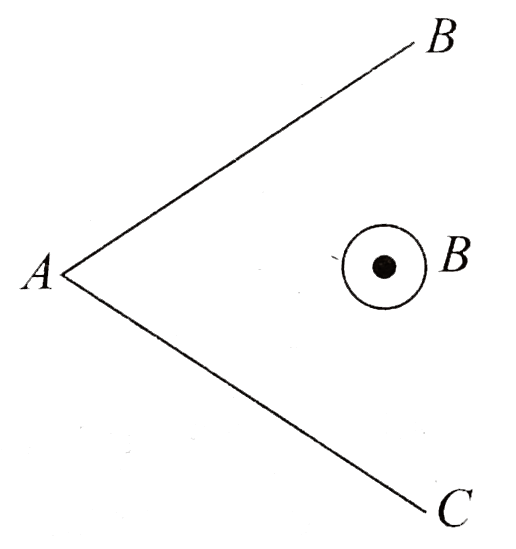
AB and AC are boundary lines within which a magnetic field B exists. If the magnetic field is absent, a charged particle of mass m and charge q must have passed through a point P on angle bisector of -BAC, at a distance r(√2) from A, if it has fallen on AB normally at a point Q such that QP =r. If the magnetic field is present, how much time the charged particle will take to come out of the magnetic field
mπBq
2mπBq
4mπBq
mπ2Bq
The correct Answer is:D
Since, QP=r,AP=r√2and∠AQP=90∘
AQ=rand∠QAP=45∘
The same logic concludes AR=r and ∠PAR=45∘
so, ∠QAR=90∘
r=mvBq
Distance travelled =πr2 ltbRgt Time=π2⋅mvBq⋅1v=mπ2Bq.

Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Multiple Correct
Explore 34 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Linked Comprehension
Explore 84 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:True and False
Explore 3 Videos
- NUCLEAR PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:NUCLEAR PHYSICSExercise:ddp.5.5
Explore 14 Videos
Similar Questions
A charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
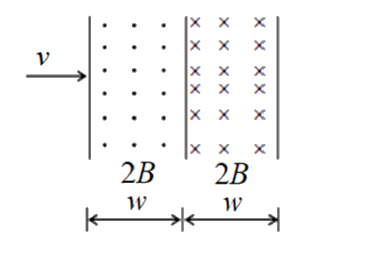
View SolutionThe figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
View SolutionA charged particle is moved along a magnetic field line. The magnetic force on the particle is
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View SolutionFigure shows a circular region of radius R in which uniform magnetic field B exists. The magnetic field is increasing at a rate dBdt. The induced electric field at a distance r from the centre for r<R is

View SolutionA charged particle of mass m is moving with a speed u in a circle of radius r. If the magnetic field induction at the centre is B, the charge on the particle is
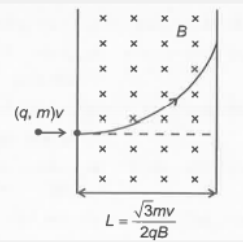
View SolutionA charge particle of mass m and charge q enters in a region of uniform magnetic field as shown in figure.The magnitude of change in linear momentum due to magnetic field will be
View SolutionA charged particle having charge q, is moving at right angles to a magnetic field. The quantity which is varying for it is-
View SolutionA charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time takeen by the particle to complete one revolution is
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View Solution