An inductor wire has some resistnce R when connected to dc. It is connected to an ac source. Now the impedance of the wire will be more than R. (ture/false)
To determine whether the statement "the impedance of the wire will be more than R" is true or false when an inductor wire with resistance R is connected to an AC source, we can analyze the situation step by step.
1. Understanding Resistance and Impedance:
- When the inductor wire is connected to a DC source, it has a resistance denoted as R.
- Resistance is a measure of how much the wire opposes the flow of direct current (DC).
2. Connecting to an AC Source:
- When the wire is connected to an AC source, the behavior changes because AC current alternates direction, and inductors respond to this change.
3. Defining Impedance:
- Impedance (Z) is the total opposition to current flow in an AC circuit and is a combination of resistance (R) and reactance.
- The formula for impedance in an inductive circuit is given by:
Z=√R2+X2L
- Here, XL is the inductive reactance, which is defined as:
XL=L⋅ω
- Where L is the inductance of the inductor and ω is the angular frequency of the AC source (ω=2πf, where f is the frequency).
4. Calculating Inductive Reactance:
- Since XL is always a positive value (as it depends on inductance and frequency), it adds to the resistance R when calculating impedance.
5. Conclusion:
- Because Z=√R2+X2L and XL is greater than zero, it follows that:
Z>R
- Therefore, the statement "the impedance of the wire will be more than R" is True.
Final Answer:
True
- When the inductor wire is connected to a DC source, it has a resistance denoted as R.
- Resistance is a measure of how much the wire opposes the flow of direct current (DC).
- When the wire is connected to an AC source, the behavior changes because AC current alternates direction, and inductors respond to this change.
- Impedance (Z) is the total opposition to current flow in an AC circuit and is a combination of resistance (R) and reactance.
- The formula for impedance in an inductive circuit is given by:
Z=√R2+X2L
- Here, XL is the inductive reactance, which is defined as:
XL=L⋅ω
- Where L is the inductance of the inductor and ω is the angular frequency of the AC source (ω=2πf, where f is the frequency).
- Since XL is always a positive value (as it depends on inductance and frequency), it adds to the resistance R when calculating impedance.
- Because Z=√R2+X2L and XL is greater than zero, it follows that:
Z>R
- Therefore, the statement "the impedance of the wire will be more than R" is True.
True
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Single Correct
63 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Solved Examples
6 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
Knowledge Check
Power dissipated in an L−C−R series circuit connected to an AC source of emf ε is
Aε2√R2+(ωL−1ωC)2RBε2[R2+(ωL−1ωC)2]RCε2R√R2+(ωL−1ωC)2Dε2R[R2+(ωL−1ωC)2]
In a series L, R, C, circuit which is connected to a.c. source. When resonance is obtained then net impedance Z will be
View SolutionThe current through an inductor of impedance 10Ω lags behind the voltage by a phase of 60∘ when just the inductor is connected to the ac source. Now the inductor is connected to a 5Ω resistance in series, then the net impedance of the circuit is
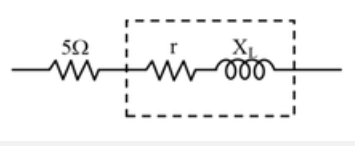
View SolutionName the colour code of the wire which is r connected to
switch for the appliance
View SolutionAn inductor of inductance L and ressistor of resistance R are joined in series and connected by a source of frequency ω. Power dissipated in the circuit is
View SolutionA 400 Ω resistor, a 3 H inductor and a 5 μF capacitor are connected in series to a 220 V, 50 Hz ac source. Calculate the :
(1) Impedance of the ciruit.
(ii) Current flowing through the circuit.
View SolutionPower dissipated in an L−C−R series circuit connected to an AC source of emf ε is
View SolutionIn the given figure , a series L-C-R circuit is connected to a variable frequency source of 230 V . The impedance and amplitude of the current at the resonating frequency will be
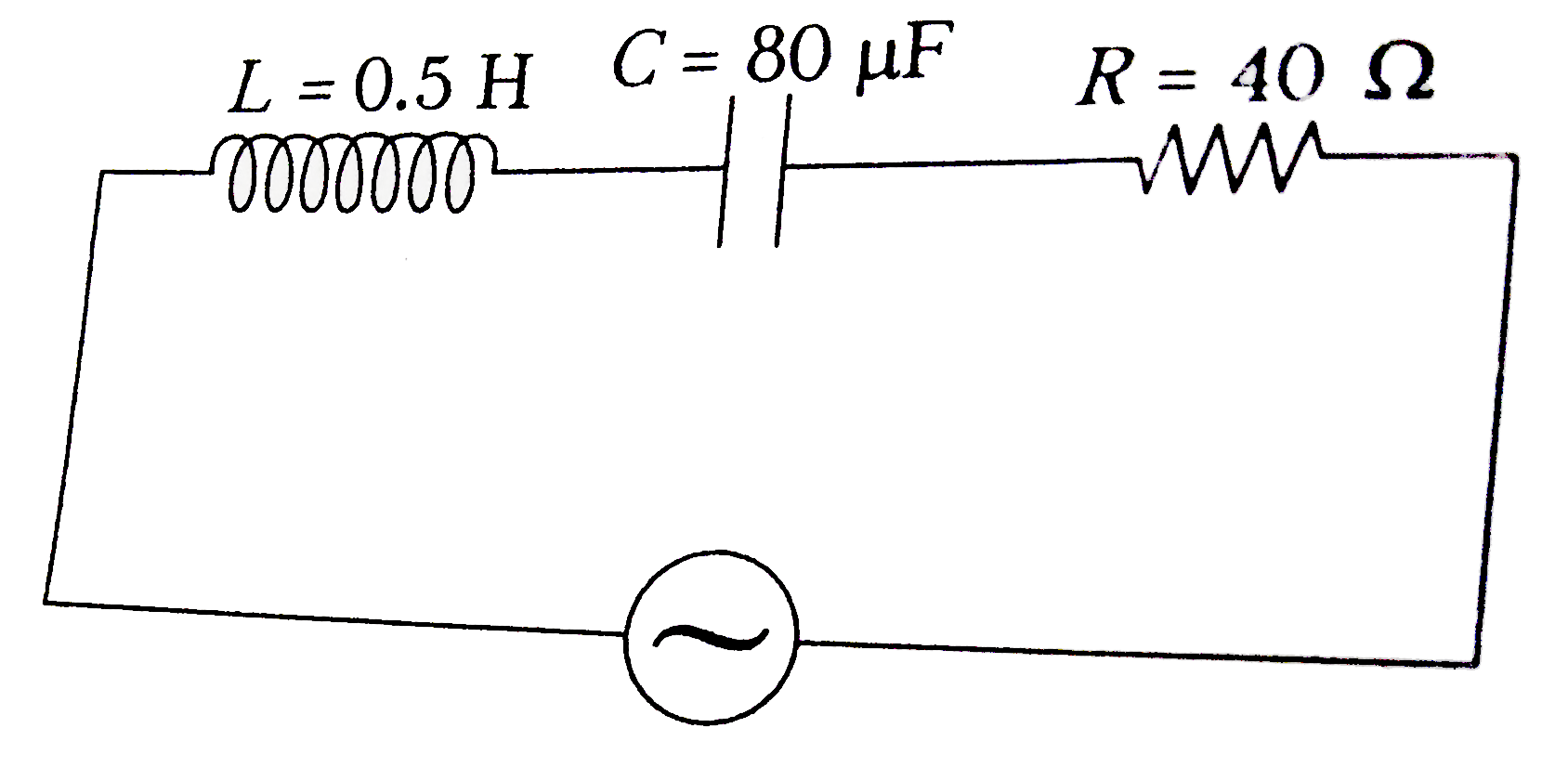
View Solution
