A voltage , E=60sin(314t), is applied across a resistor of 20Ω. What will be the reading of Irms.
(a) in an ac ammeter?
(b) in an ordinary moving coil ammeter in series with the resistor?
To solve the problem, we need to find the root mean square (RMS) current, Irms, for both an AC ammeter and an ordinary moving coil ammeter when a voltage E=60sin(314t) is applied across a resistor of 20Ω.
1. Identify the Peak Voltage:
The given voltage can be compared with the standard form E=E0sin(ωt).
Here, E0=60V.
2. Calculate the RMS Voltage:
The relationship between the peak voltage E0 and the RMS voltage Erms is given by:
Erms=E0√2
Substituting the value of E0:
Erms=60√2≈42.4V
3. Calculate the RMS Current for AC Ammeter:
The RMS current Irms can be calculated using Ohm's law:
Irms=ErmsR
where R=20Ω.
Substituting the values:
Irms=42.420≈2.12A
4. Determine the Reading in an Ordinary Moving Coil Ammeter:
An ordinary moving coil ammeter measures the average value of the current. For AC current, the average value over one complete cycle is zero. Therefore, the reading in an ordinary moving coil ammeter will be:
Iaverage=0A
Final Answers:
(a) The reading of Irms in an AC ammeter is approximately 2.12 A.
(b) The reading of Irms in an ordinary moving coil ammeter in series with the resistor is 0 A.
The given voltage can be compared with the standard form E=E0sin(ωt).
Here, E0=60V.
The relationship between the peak voltage E0 and the RMS voltage Erms is given by:
Erms=E0√2
Substituting the value of E0:
Erms=60√2≈42.4V
The RMS current Irms can be calculated using Ohm's law:
Irms=ErmsR
where R=20Ω.
Substituting the values:
Irms=42.420≈2.12A
An ordinary moving coil ammeter measures the average value of the current. For AC current, the average value over one complete cycle is zero. Therefore, the reading in an ordinary moving coil ammeter will be:
Iaverage=0A
(a) The reading of Irms in an AC ammeter is approximately 2.12 A.
(b) The reading of Irms in an ordinary moving coil ammeter in series with the resistor is 0 A.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Solved Examples
6 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 5.1
15 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
An alternating voltage E=E0sinωt , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
View SolutionAn alternating voltage V=140 sin 50 t is applied to a resistor of resistance 10 Ω. This voltage produces △H heat in the resistor in time △t. To produce the same heat in the same time, rquired DC current is
View Solution
Knowledge Check
A alternating voltage given by V=140sin314t is connected across a pure resistor of 50 ohm. Find the rms current through the resistor.
A1.98AB5.63AC3.536AD49.39A
An alternating voltage V=140 sin 50 t is applied to a resistor of resistance 10 Ω. This voltage produces △H heat in the resistor in time △t. To produce the same heat in the same time, rquired DC current is
View SolutionAn alternating voltage given by V=140sin314t is connected across a pure resistor of 50 ohm. Find (i) the frequency of the source. (ii) the rms current thought the resistor.
View SolutionAn alternating voltage given by V=70sin100πt is connected across a pure resistor of 25Ω. Find
(i) the frequency of the source.
(ii) the rms current through the resistor.
View SolutionThe value of escape speed from the surface of earth is
View SolutionAn a.c., source of emf ε=200sinωt is connected to a resistor of 50Ω. Calculate:
Root mean square (rms) value of emf
View SolutionAn a.c., source of emf ε=200sinωt is connected to a resistor of 50Ω. Calculate:
Average current (Iavg)
View SolutionA constant 60V dc supply is connected across two resistors of resistance 400kΩ and 200kΩ. What is the reading of the voltmeter, also of resistance 200kΩ, when connected across the second resistor as shows in Fig. 6.48?
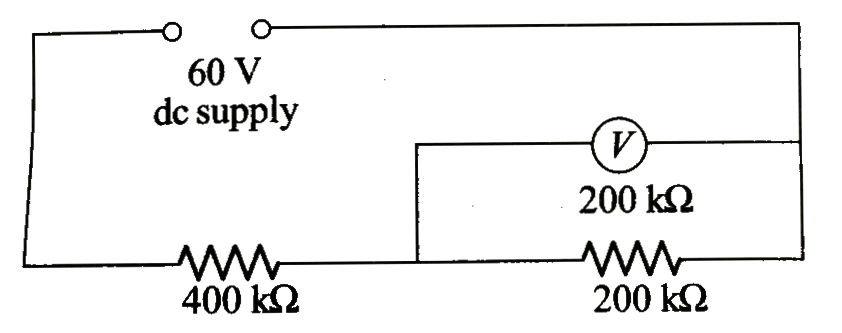
View Solution
