A coil of wire having inductance and resistance has a conducting ring placed coaxially within it. The coil is connected to a battery at time t=0, so that a time-dependent current 11(t) starts following through the coil. If I2(t) is the current induced in the ring, and B (t) is the magnetic field at the axis of the coil due to I1(t) then as a function of time (t>0), the product I2(t)B(t)
increases with time
decreases with time
does not vary with time
passes through a mximum
The correct Answer is:D
To solve the problem step by step, we will analyze the situation involving the coil, the induced current in the ring, and the magnetic field produced by the coil.
Step 1: Understand the System
We have a coil with inductance L and resistance R connected to a battery at t=0. A current I1(t) starts flowing through the coil. Inside this coil, there is a conducting ring placed coaxially.
Step 2: Determine the Magnetic Field B(t)
The magnetic field at the axis of the coil due to the current I1(t) can be expressed as:
B(t)=μ0nI1(t)
where μ0 is the permeability of free space and n is the number of turns per unit length of the coil.
Step 3: Find the Induced EMF in the Ring
The induced electromotive force (EMF) E in the ring is due to the change in magnetic flux through it. The magnetic flux Φ through the ring is given by:
Φ=B(t)⋅A
where A is the area of the ring. The induced EMF can be expressed as:
E=−dΦdt=−AdBdt
Since B(t) depends on I1(t), we can write:
E=−Aμ0ndI1dt
Step 4: Find the Induced Current I2(t)
The induced current I2(t) in the ring can be found using Ohm's law:
I2(t)=ER=−Aμ0nRdI1dt
Let’s denote the constant k1=−Aμ0nR, then:
I2(t)=k1dI1dt
Step 5: Determine I1(t)
For an LR circuit, the current I1(t) can be expressed as:
I1(t)=I0(1−e−tτ)
where τ=LR is the time constant.
Step 6: Differentiate I1(t)
Now, we differentiate I1(t) to find dI1dt:
dI1dt=I0τe−tτ
Step 7: Substitute dI1dt into I2(t)
Substituting dI1dt into the expression for I2(t):
I2(t)=k1⋅I0τe−tτ
Step 8: Find the Product I2(t)B(t)
Now, we can find the product I2(t)B(t):
I2(t)B(t)=(k1⋅I0τe−tτ)(μ0nI1(t))
Substituting I1(t):
I2(t)B(t)=k1⋅I0τe−tτ⋅μ0n⋅I0(1−e−tτ)
Step 9: Analyze the Behavior of I2(t)B(t)
As t approaches 0, I2(t)B(t) approaches 0. As t approaches infinity, I2(t)B(t) also approaches 0. Therefore, there is a maximum value at some point in time.
Conclusion
The product I2(t)B(t) passes through a maximum value as time progresses.
We have a coil with inductance L and resistance R connected to a battery at t=0. A current I1(t) starts flowing through the coil. Inside this coil, there is a conducting ring placed coaxially.
The magnetic field at the axis of the coil due to the current I1(t) can be expressed as:
B(t)=μ0nI1(t)
where μ0 is the permeability of free space and n is the number of turns per unit length of the coil.
The induced electromotive force (EMF) E in the ring is due to the change in magnetic flux through it. The magnetic flux Φ through the ring is given by:
Φ=B(t)⋅A
where A is the area of the ring. The induced EMF can be expressed as:
E=−dΦdt=−AdBdt
Since B(t) depends on I1(t), we can write:
E=−Aμ0ndI1dt
The induced current I2(t) in the ring can be found using Ohm's law:
I2(t)=ER=−Aμ0nRdI1dt
Let’s denote the constant k1=−Aμ0nR, then:
I2(t)=k1dI1dt
For an LR circuit, the current I1(t) can be expressed as:
I1(t)=I0(1−e−tτ)
where τ=LR is the time constant.
Now, we differentiate I1(t) to find dI1dt:
dI1dt=I0τe−tτ
Substituting dI1dt into the expression for I2(t):
I2(t)=k1⋅I0τe−tτ
Now, we can find the product I2(t)B(t):
I2(t)B(t)=(k1⋅I0τe−tτ)(μ0nI1(t))
Substituting I1(t):
I2(t)B(t)=k1⋅I0τe−tτ⋅μ0n⋅I0(1−e−tτ)
As t approaches 0, I2(t)B(t) approaches 0. As t approaches infinity, I2(t)B(t) also approaches 0. Therefore, there is a maximum value at some point in time.
The product I2(t)B(t) passes through a maximum value as time progresses.
Topper's Solved these Questions
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Archives (multiple Correct)
Explore 3 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Archives (linked Compreshension)
Explore 8 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Archives (fills In The Blanks)
Explore 3 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
Similar Questions
Knowledge Check
A circular coil of 25 turns and radius 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of the coil. If the current in the coil is 6 A then total torque acting on the coil is
AzeroB3.4 NmC3.8 NmD4.4 Nm
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
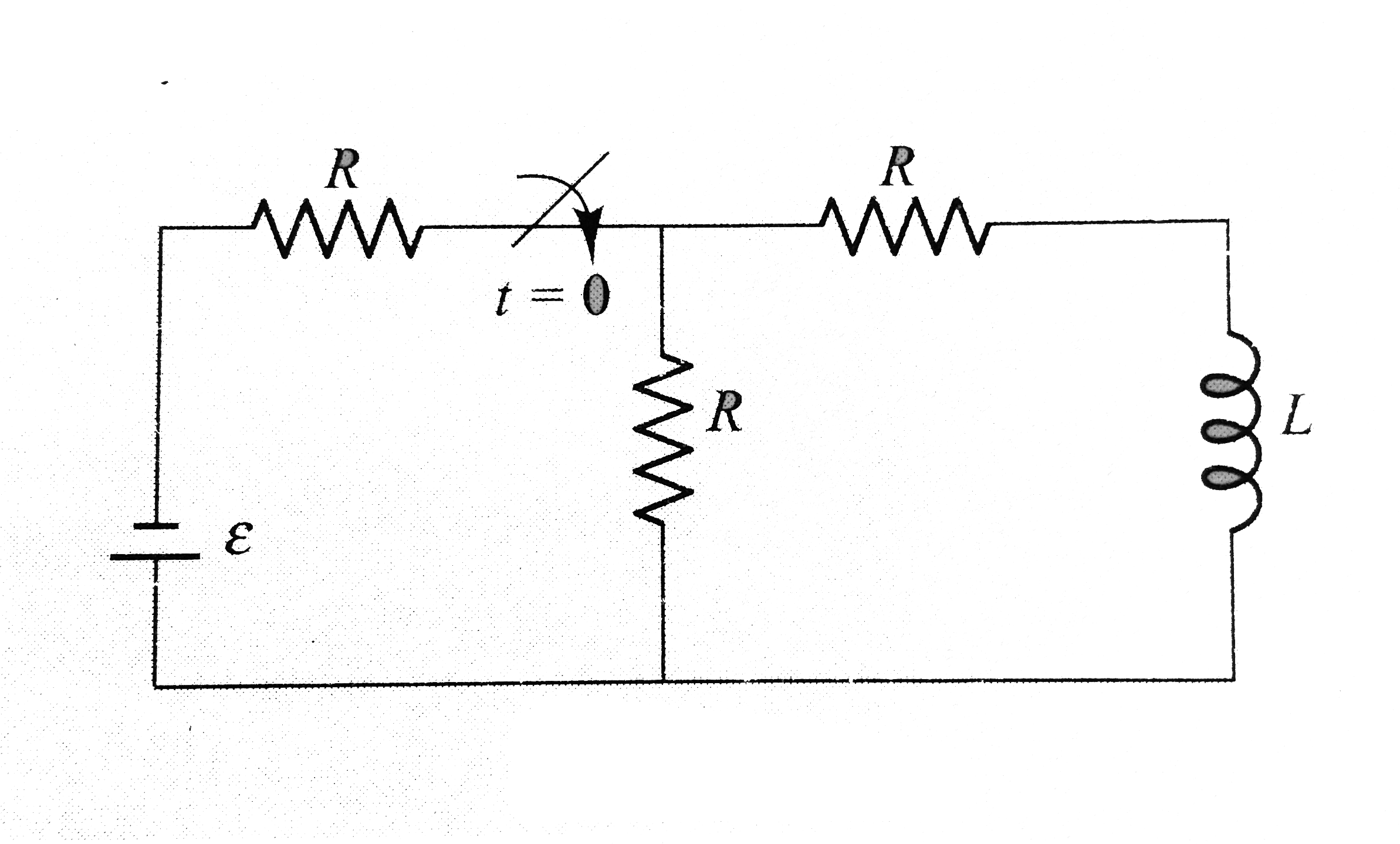
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 2I is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionA coil having inductance and L and resistance R is connected to a battery of emf ∈ at t=0. If t1 and t2 are time for 90% and 99% completion of current growth in the circuit, then t1t2 will be-
View SolutionThe current in the inner coil is I=2t2. Find the heat developed in the outer coil between t =0 and t seconds. The resistance of the outer coil is R and take b>>a.

View SolutionA coil of inductanece 5H is joined to a cell of emf 6V through a resistance 10Ω at time t=0. The emf across the coil at time t=ln√2 s is:
View SolutionIn the following circuit the switch is closed at t=0.Intially there is no current in inductor.Find out current the inductor coil as a function of time.
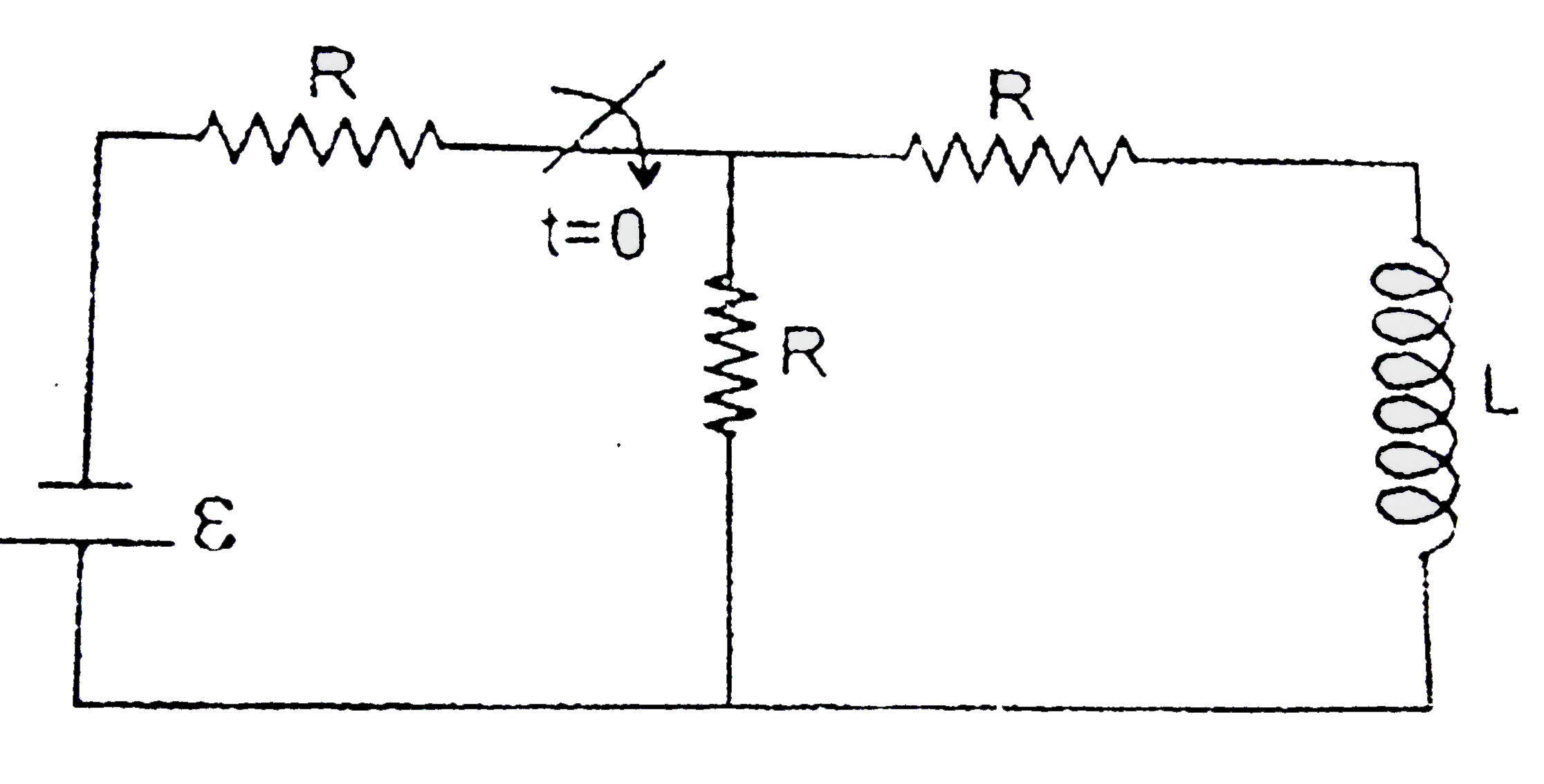
View Solution