In the circuit shows in Fig. the battery has negligible internal resistance. Show that the current in the circuit through the battery rises instanlty to its steady state value E/R when the switch is closed, provided that resistance R is √L/C.

Let the currents through inductive branch and capacitive branch be IL and IC, respectively. Then the current through the battery, from KCL, is I=IL+IC.
Since the battery is connected in parallel to the RL and RC branches of the circuit, the current in the RL branch is unaffected by the presence of the RC branch, so
IL=ER[1−e−(R/L)t]and IC=ERe−(t/RC)
Hence, the current through battery is I=ER[1−e−(R/L)t+e−(t/RC)]
If the current has to reach its final value E/R instananeously, the exponitial terms must cancel out, i.e.,
e−(t/τL)=e−(t/τC), which is possible if τL=τC.
L/R=RC,R=√(L/C)
For at t>0, this is the desired result.
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Solved Examples
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercise 4.1
24 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
Knowledge Check
A battery having 12V emf and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 1A, then the resistance of resistor and lost voltage of the battery when circuit is closed will be
A7Ω,7VB8Ω,8VC9Ω,9VD9Ω,10V
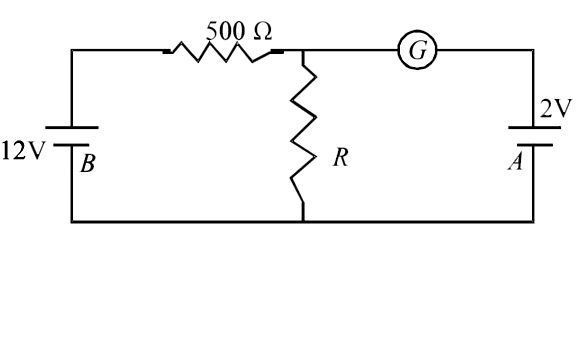
In the circuit shown, the galvanometer shows zero current. The value of resistance R is :
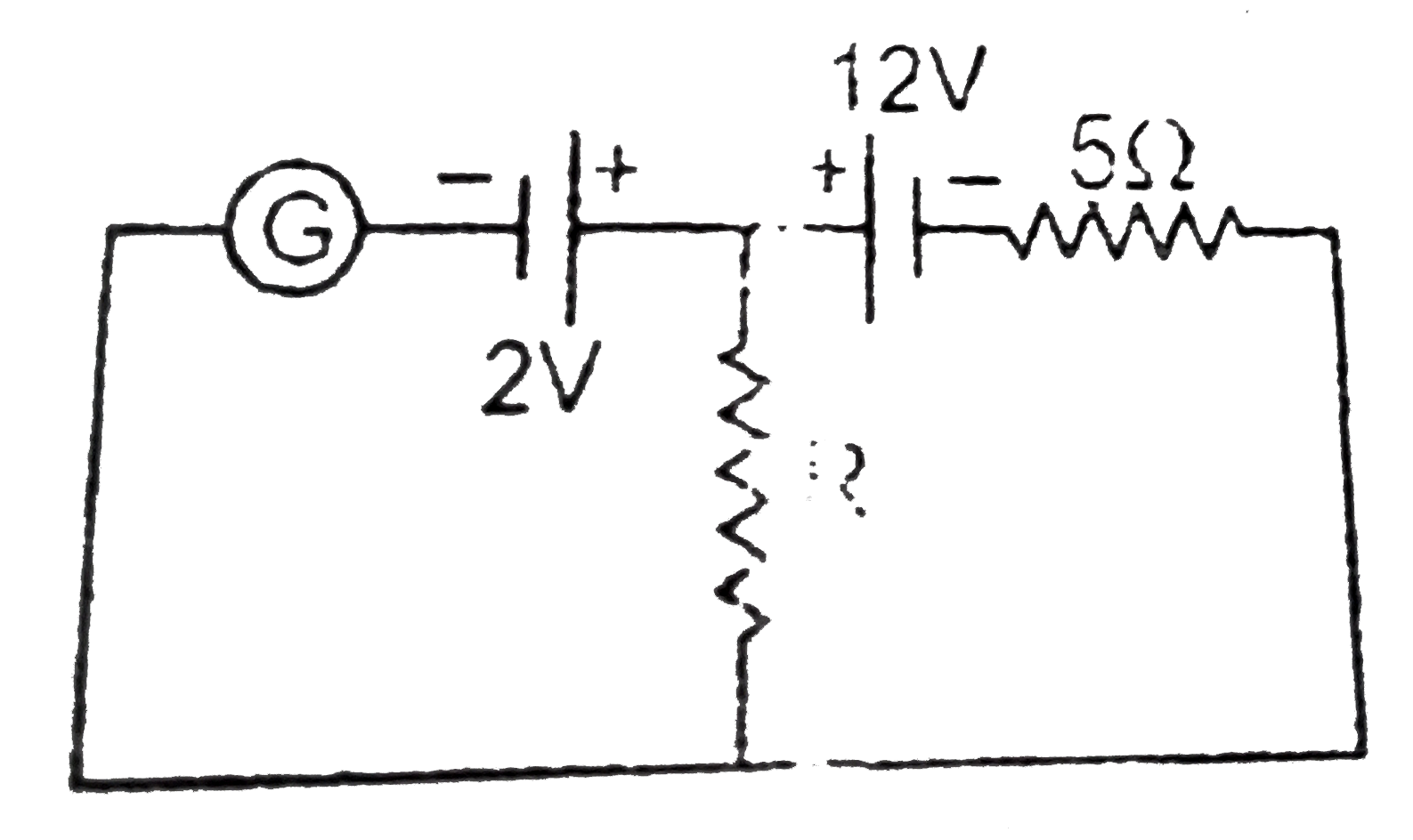
View SolutionIn the circuit, the galvanometer G shows zero deflection. If the batteries A and b have negligible internal resistance, the value of the resistor R will be -
View SolutionA 3 volt battery with negligible internal resistance is connected in a circuit as shown in the figure. The current I, in the circuit will be

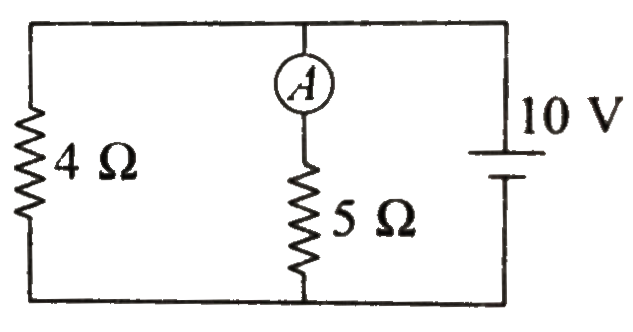
View SolutionIn the circuit shown below, E is a battery of emf 6 V and internal resistance 1Ω. Find the reading of the ammeter A. if it has negligible resistance :
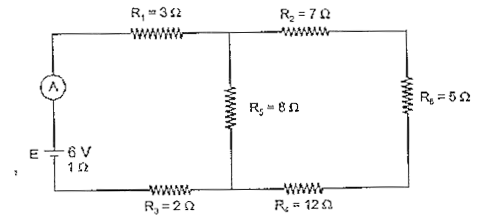
View SolutionAssume that the batteries in figure have negligible internal resistance. Find
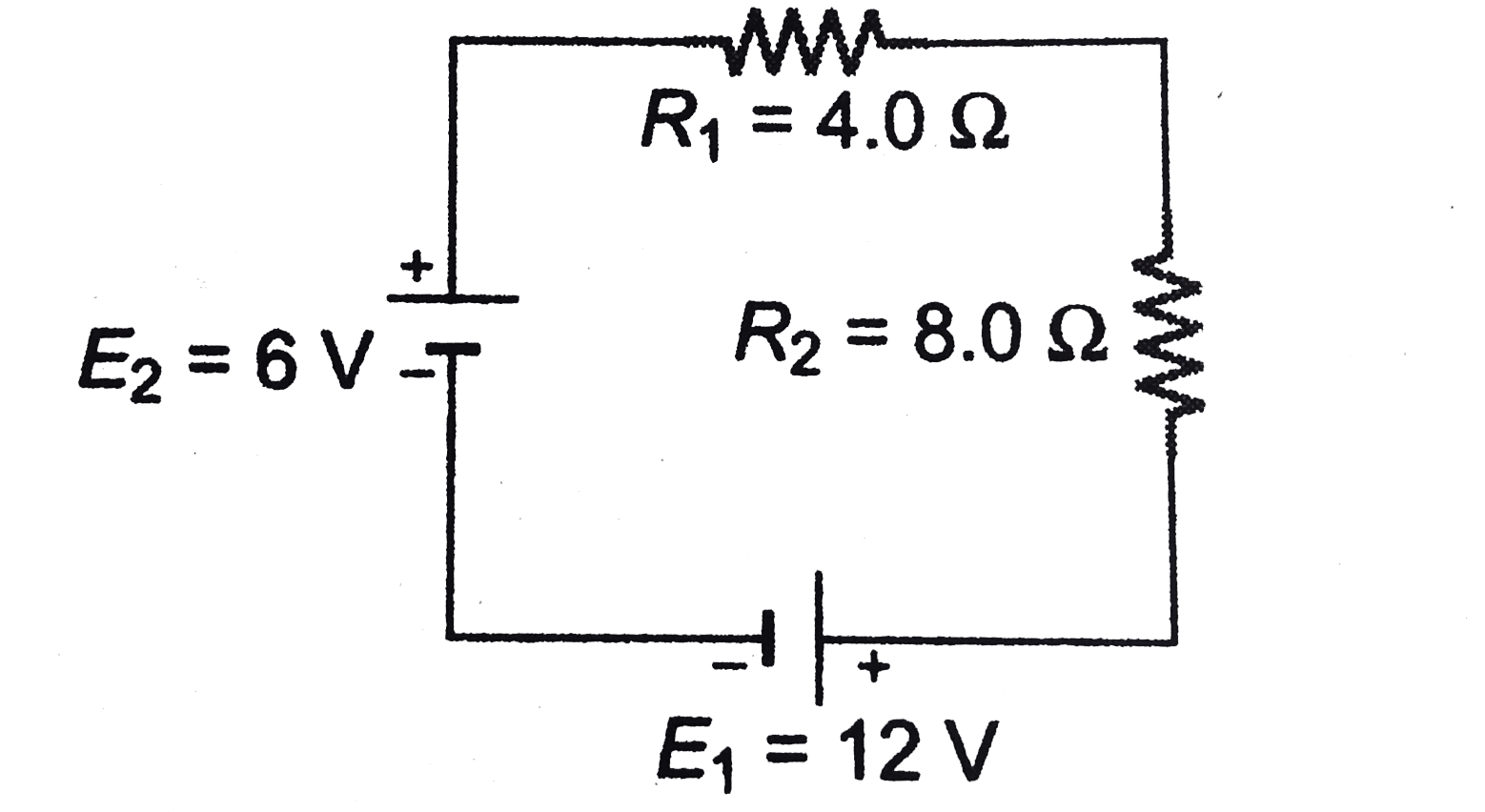
a. the current in the circuit,
(b) the power dissipated in each resistor and
(c) the power of each battery, stating whether energy is supplied by or absorbed by it
View SolutionIn the following circuit the value of current i through the battery just after switch S is closed is
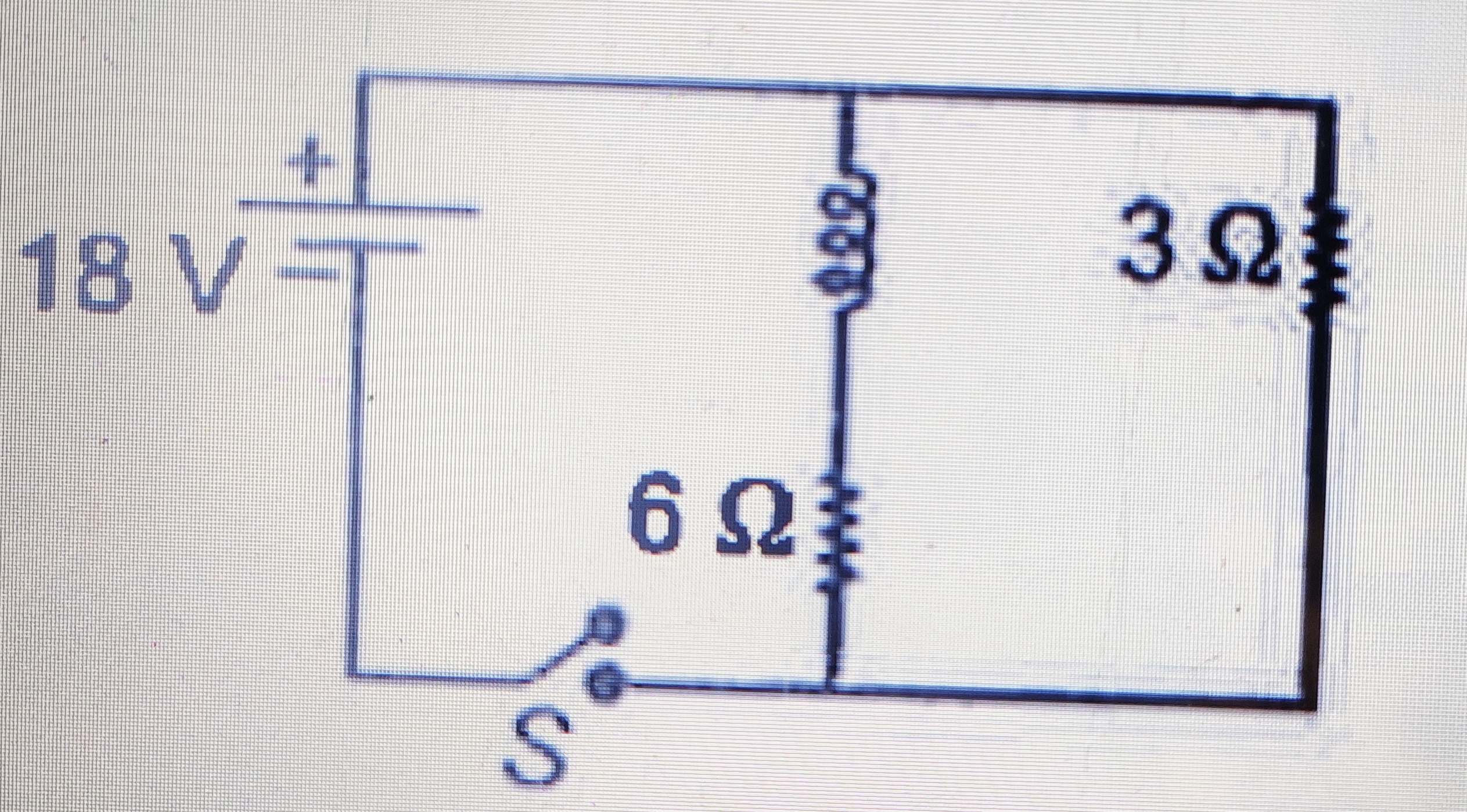
View SolutionThe figure shows three circuits with identical batteries, inductors and resistance . Rank the circuits in decreasing order, according to the current through the battery just after the switch is closed
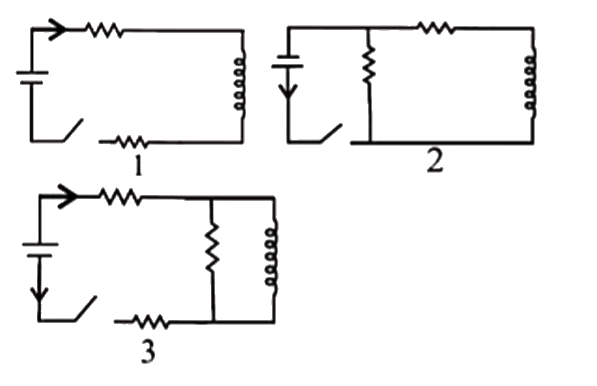
View Solution