In the circuit shown in Fig. the capacitor has capacitance C=20μF and is initially charged to 100V with the polarity shown. The resistor R0 has resistance 10Ω. At time t=0, the switch is closed. The smaller circuit is not connected in any way to teh larger one. the wire of the smaller circuit has a resistance of 1.0Ωm−1 and contains 25 loops. the larger circuit is a rectangle 2.0m by 4.0m, while the smaller one has dimensions a=10.0cm and b=20.0cm. the distance cis 5.0cm. (The figure is not drawn to scale.) Both circuit are held stationary. Assume that only the wire nearest to teh smaller circuit produces. an appreciable magnetic field through it.

The direction of current in the smaller circuit is
(a) clockwise
(b) anticlockwise
( c) always changes with time
(d) cannot be calculated
The correct Answer is:B
(b) The large circiut is a with a time constant of
τ=RC=(10Ω)(20×10−6F)=200μs.
Thus, the currnt as a function of time is
I=(100V10Ω)e−t200μs
At t=200ms, we obtain
I=(10A)(e−1)=3.7A.
Assuming that only the long wire nearest the small loop produces an appreciable magnetic flux through the small loop,
ΦB=∫c+acμ0ib2πdr=μ0ib2π1n(1+ac) ltbr> So the emf induced in the small loop at t=200ms
ε=−dΦdt=−μ0ib2π1n(1+ac)didt
=−(4π×10−7(Wb)A×m2)(0.200m)2π×1n(3.0)(−3.7A200×10−6s)
Thus, the induced current in the small loop is
i=εR=0.81mV25(0.600m)(1.0Ω/m)=54μA. ltbr> Initially current in large loop is maximum and afterwards decreases. Hence flux through the smaller loop decreases with time. The induced current will act to oppose the decreases in flux from the large loop. Thus, the induced current flows counterclockwise .
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Integer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Fill In The Blanks
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
In the circuit shown in Fig. the capacitor has capacitance C=20μF and is initially charged to 100V with the polarity shown. The resistor R0 has resistance 10Ω. At time t=0, the switch is closed. The smaller circuit is not connected in any way to teh larger one. the wire of the smaller circuit has a resistance of 1.0Ωm−1 and contains 25 loops. the larger circuit is a rectangle 2.0m by 4.0m, while the smaller one has dimensions a=10.0cm and b=20.0cm. the distance cis 5.0cm. (The figure is not drawn to scale.) Both circuit are held stationary. Assume that only the wire nearest to teh smaller circuit produces. an appreciable magnetic field through it.

The current in the circuit 200ms after closing S is
View SolutionIn the circuit shown in Fig. the capacitor has capacitance C=20μF and is initially charged to 100V with the polarity shown. The resistor R0 has resistance 10Ω. At time t=0, the switch is closed. The smaller circuit is not connected in any way to teh larger one. the wire of the smaller circuit has a resistance of 1.0Ωm−1 and contains 25 loops. the larger circuit is a rectangle 2.0m by 4.0m, while the smaller one has dimensions a=10.0cm and b=20.0cm. the distance cis 5.0cm. (The figure is not drawn to scale.) Both circuit are held stationary. Assume that only the wire nearest to teh smaller circuit produces. an appreciable magnetic field through it.

The curent in the smaller circuit 200μs after closing S is
View SolutionIn the circuit shown in fig. the cell has emf 10V and internal resistance 1Ω
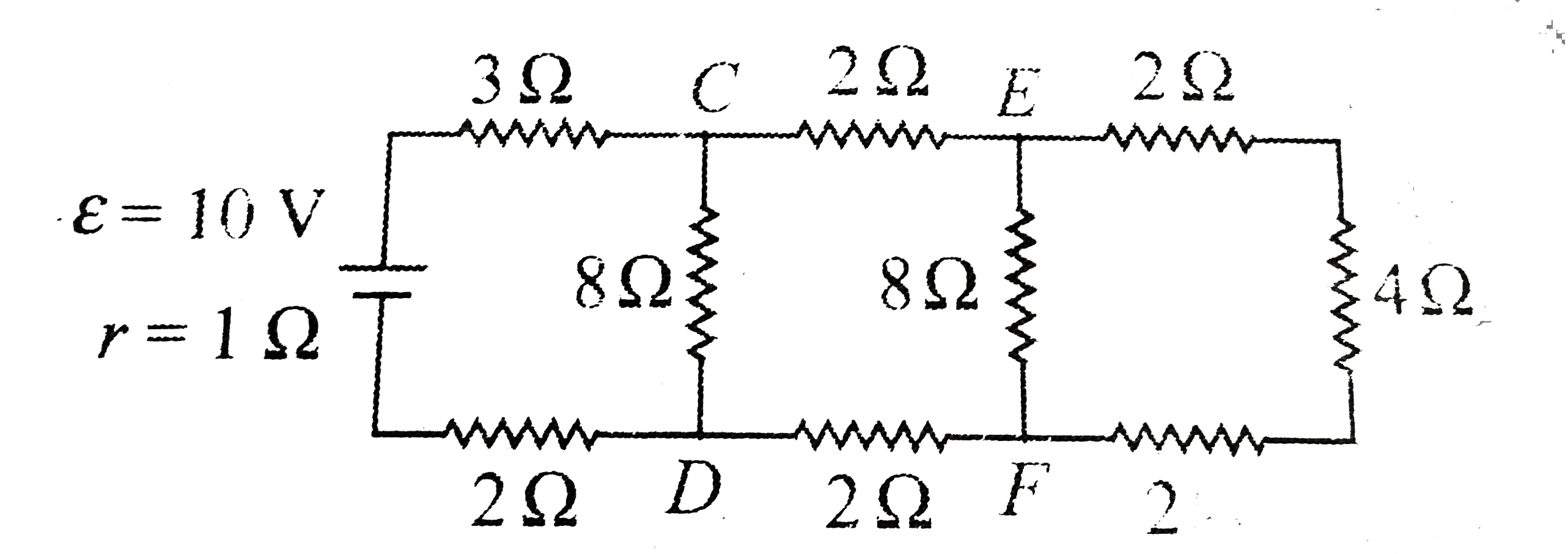
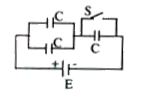
View SolutionIn the circuit shown, each capacitor has a capacitance C. The emf of the cell is E. If the switch S is closed
View SolutionThe charge on the capacitor of capacitance 10μF in steady state condition in the circuit shown is
_PHY_E05_271_Q01.png)
View SolutionA wire of length 1 m and radius 0.1mm has a resistance of 100(Ω).Find the resistivity of the material .
View SolutionIn the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is
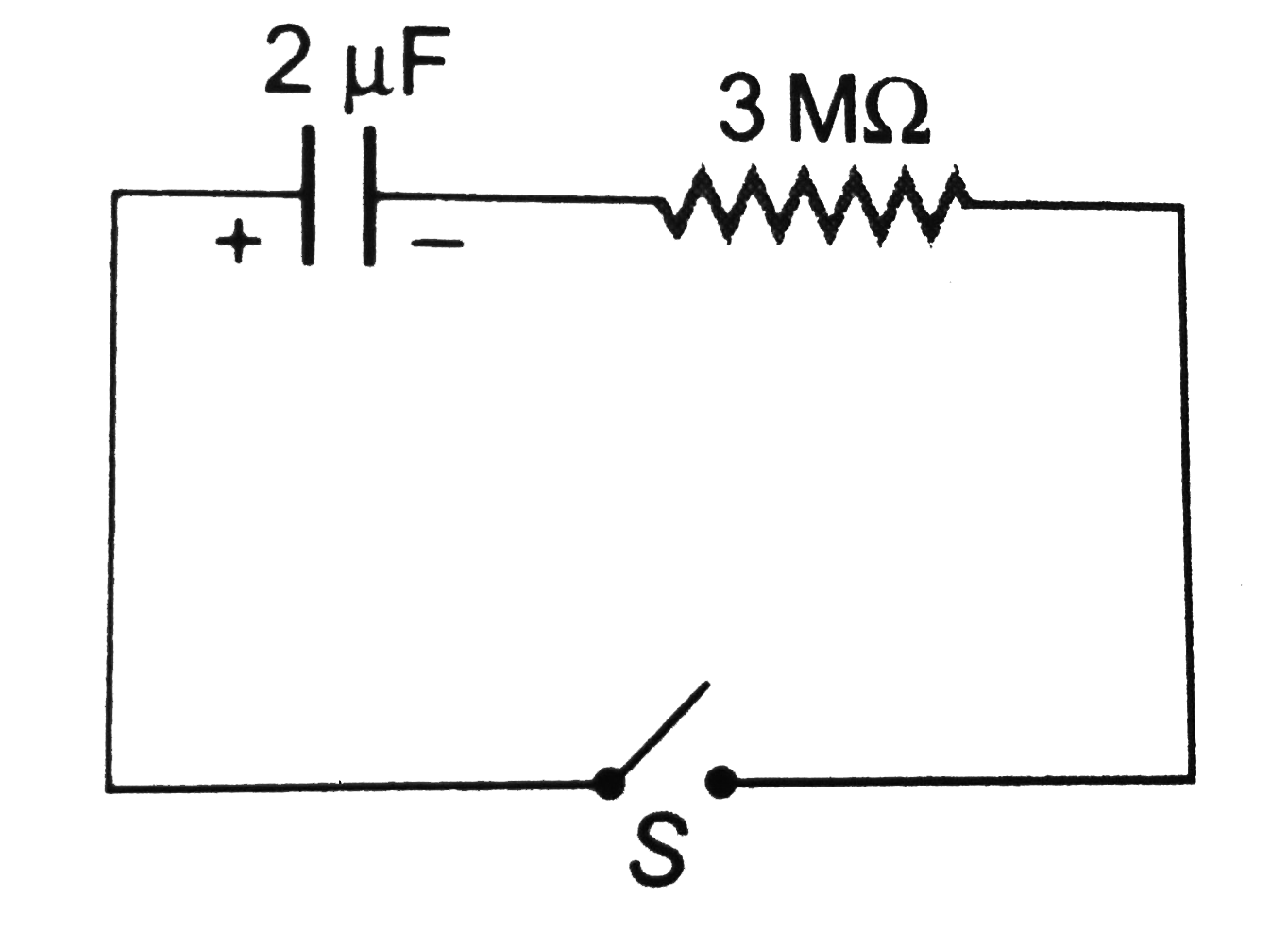
View SolutionIn the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
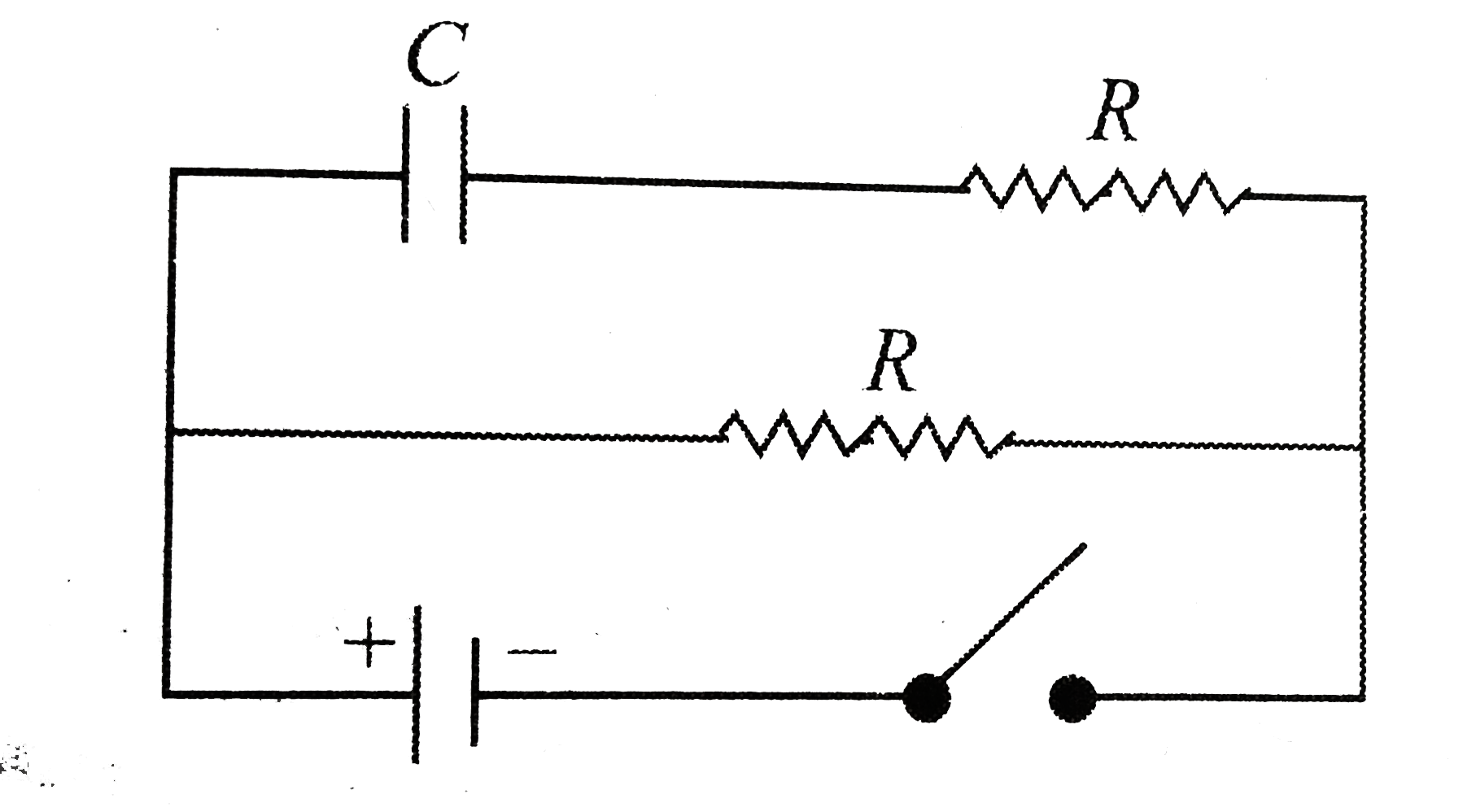
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
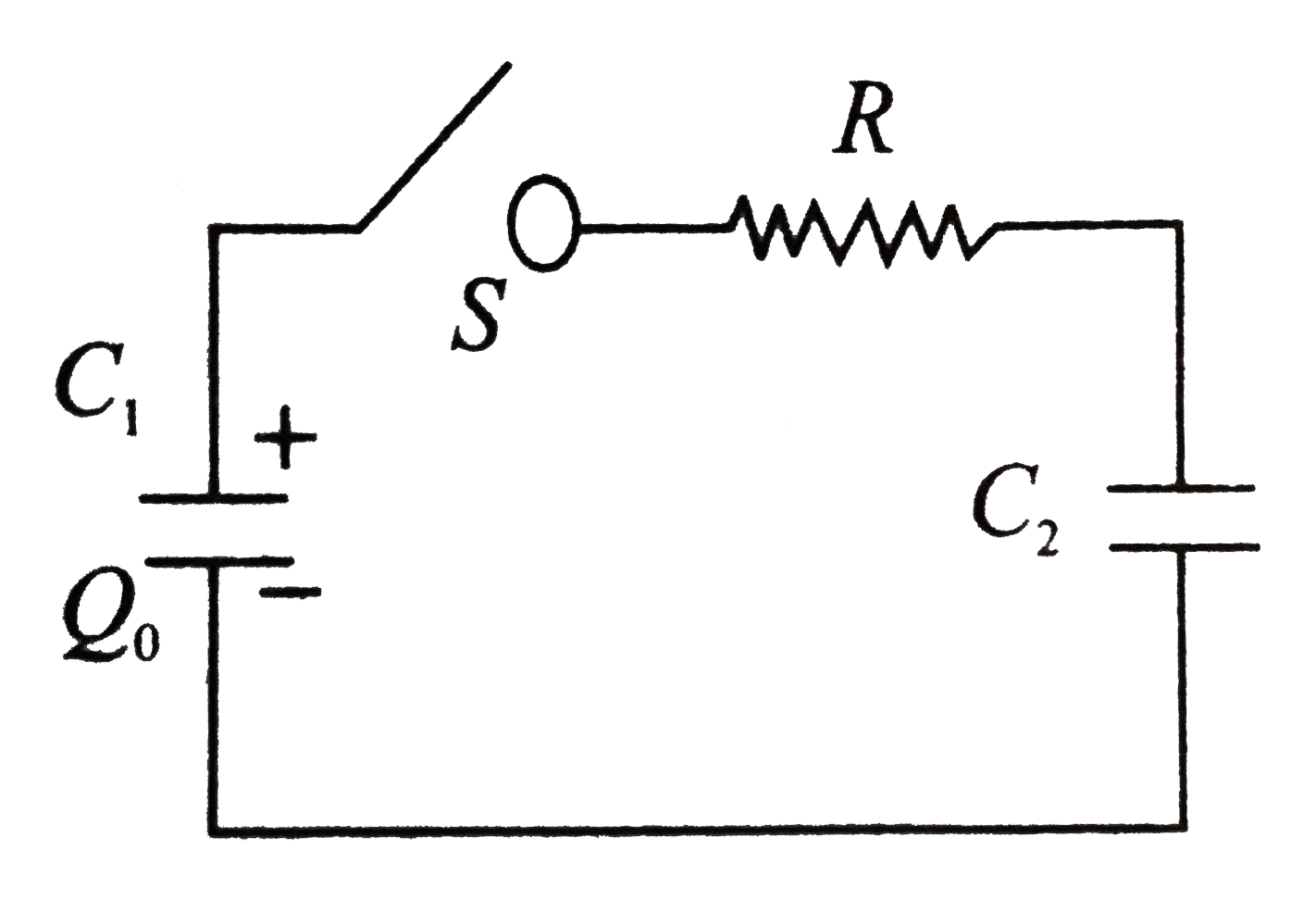
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
View Solution
