A metal rod 1.5m long rotates about its one end in a vertical plane at right angles to the magnetic meridian. If the frequency of rotation is 20revs−1, find the emf induced between the ends of the rod (BH=0.32G).
To find the induced EMF between the ends of a rotating metal rod, we can follow these steps:
Step 1: Identify the given values
- Length of the rod (L) = 1.5 m
- Frequency of rotation (ν) = 20 rev/s
- Horizontal component of the magnetic field (B_H) = 0.32 G
Step 2: Convert the magnetic field from Gauss to Tesla
1 Gauss (G) = 10−4 Tesla (T)
So,
BH=0.32G=0.32×10−4T=3.2×10−5T
Step 3: Use the formula for induced EMF
The formula for the induced EMF (E) when a rod rotates in a magnetic field is given by:
E=12BHL2ω
Where:
- ω is the angular frequency in radians per second.
Step 4: Convert frequency to angular frequency
Angular frequency ω is related to frequency ν by:
ω=2πν
Substituting the value of frequency:
ω=2π×20rev/s=40πrad/s
Step 5: Substitute the values into the EMF formula
Now, substituting the values into the EMF formula:
E=12×(3.2×10−5T)×(1.5m)2×(40πrad/s)
Calculating (1.5m)2:
(1.5)2=2.25m2
Now substituting this back into the equation:
E=12×(3.2×10−5)×2.25×(40π)
Step 6: Calculate the EMF
Calculating the numerical values:
- First calculate 40π:
40π≈125.66
Now substituting:
E=12×(3.2×10−5)×2.25×125.66
Calculating:
E≈12×3.2×2.25×125.66×10−5
E≈12×3.2×2.25×125.66×10−5
E≈4.5×10−3V=4.5mV
Final Answer
The induced EMF between the ends of the rod is approximately 4.5 mV.
---
- Length of the rod (L) = 1.5 m
- Frequency of rotation (ν) = 20 rev/s
- Horizontal component of the magnetic field (B_H) = 0.32 G
1 Gauss (G) = 10−4 Tesla (T)
So,
BH=0.32G=0.32×10−4T=3.2×10−5T
The formula for the induced EMF (E) when a rod rotates in a magnetic field is given by:
E=12BHL2ω
Where:
- ω is the angular frequency in radians per second.
Angular frequency ω is related to frequency ν by:
ω=2πν
Substituting the value of frequency:
ω=2π×20rev/s=40πrad/s
Now, substituting the values into the EMF formula:
E=12×(3.2×10−5T)×(1.5m)2×(40πrad/s)
(1.5)2=2.25m2
E=12×(3.2×10−5)×2.25×(40π)
Calculating the numerical values:
- First calculate 40π:
40π≈125.66
E=12×(3.2×10−5)×2.25×125.66
E≈12×3.2×2.25×125.66×10−5
E≈12×3.2×2.25×125.66×10−5
E≈4.5×10−3V=4.5mV
The induced EMF between the ends of the rod is approximately 4.5 mV.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Solved Example5videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.115videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
Similar Questions
A metal rod length l rotates about on end with a uniform angular velocity ω. A uniform magnetic field →B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they moving in circular paths.
View SolutionA metal disc of radius 200 cm is rotated at a constant angular speed of 60rads−1 in a plane at right angles to an external field of magnetic induction 0.05Wbm−2. Find the e.m.f. induced between the centre and a point on the rim.
View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View SolutionThe figure shown an L-shaped rod rotating about its end O in a plane perpendicular to a magnetic field B. The part OA of rod is non conducting while AB is conducting the emf induced between A and B is
 View Solution
View SolutionA copper rod AB-of length / pivoted at one end A, rotates at constant angular velocity ω, at right angles to a uniformn magnetic field of induction B. The emf, developed between the mid point of the rod and end B is
View SolutionA conducting rod of unit length moves with a velocity of 5m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.4T. Find the emf induced between the ends of the stick.
View SolutionA wire of length 10cm translates in a direction making an angle of 60∘ with its length. The plane of motion is perpendicular ot a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation of 20 cm s^(-1).
View SolutionA wire of length 10cm translates in a direction making an angle of 60∘ with its length. The plane of motion is perpendicular ot a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation of 20cms−1.
View SolutionA conducting rod of length / is rotating about point Pin a uniform transverse magnetic field B0 as shown in the figure. If angular speed of the rod is ω0 then the magnitude of induced emf across the ends of the rod will be (PA=2l3andPB=l3)
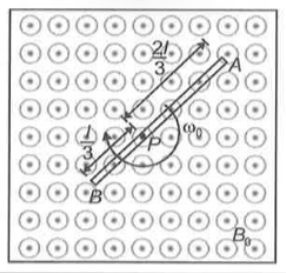 View Solution
View SolutionA metallic rod of length 'l' is tied to a string of length 2l and made to rotate with angular speed w on a horizontal table with one end of the string fixed. If there is a vertical magnetic field 'B' in the region, the e.m.f. Induced across the ends of the rod is
 View Solution
View Solution
