Consider the motion of a positive point charge in a region where there are simultaneous uniform eletric and magnetic field and . At time , this charge has velocity v in the x-y-plane making an angle with the x-axis. Which of the following option(s) is (are) correct for time
a. If the charge moves in a circular path in the xy-plane.
the charge undergoes helical motion with constant pitch along the y-axis.
c. If the charge undergoes helicalmotion with its pitch increasing with time along the -axis.
d. If the charge undergoes linear but accelerated motion along the -axis.
If , the charge moves in a circular path in the x-z plane
If , the charge undergoes helical motion with constant pitch along the y-axis
If , the charge undergoes helical motion with its pitch increasing with time, along the y-axis
If , the charge undergoes linear but accelerated motion along the y-axis
The correct Answer is:(c,d)
If then due to magnetic force path is circular but due
to force will have accelerated motion along y-axis. So
combined path of q will be a helical
path with variable pitch so (a) and
(b) are wrong.
If , then dut to , path
is circular and due to and v sin
, q has accelerated motion along
y-axis so combined path is a helical
path with variable pitch (C) is correct.
If and due to motion is accelerated along
y-axis. (d)

Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Comprehension
2 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Integer
1 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Single Correct
18 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A charge particle is moving along positive y-axis in uniform electric and magnetic fields
E=E0ˆk
and B=B0ˆi
Here E0 and B0 are positive constants.choose the correct options.
View SolutionA particle of mass m and charge q is lying at the origin in a uniform magnetic field B directed along x-axis. At time t = 0, it is given a velocity v0, at an angleθ with the y-axis in the xy-plane. Find the coordinates of the particle after one revolution.
View SolutionA proton moves at a constant velocity of 50ms along the x-axis, in uniform electric and magnetic fields. The magnetic field is B=(2.0mT)ˆj. What is the electric field?
View SolutionElectric field and magnetic field n a region of space is given by E=E0ˆj and B=B0ˆj. A particle of specific charge alpha is released from origin with velocity v=v0ˆi. Then path of particle
View SolutionA positively charged particle is moving along the positive x-axis in a unifom electric field→E=E0ˆj and magnetic field →B=B0ˆk (where E0 and B0 are positive constants), then
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass m and charge q is given a velocity v=vj+vk. Find the minimum speed of the particle and the time when it happens so.

View SolutionUniform electric field exists in a region and is given by →E=E0ˆi+E0ˆj. There are four points A(−a,0),B(0,−a),C(a,0),andD(0,a) in the xy plane. Which of the following is the correct relation for the electirc potential?
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
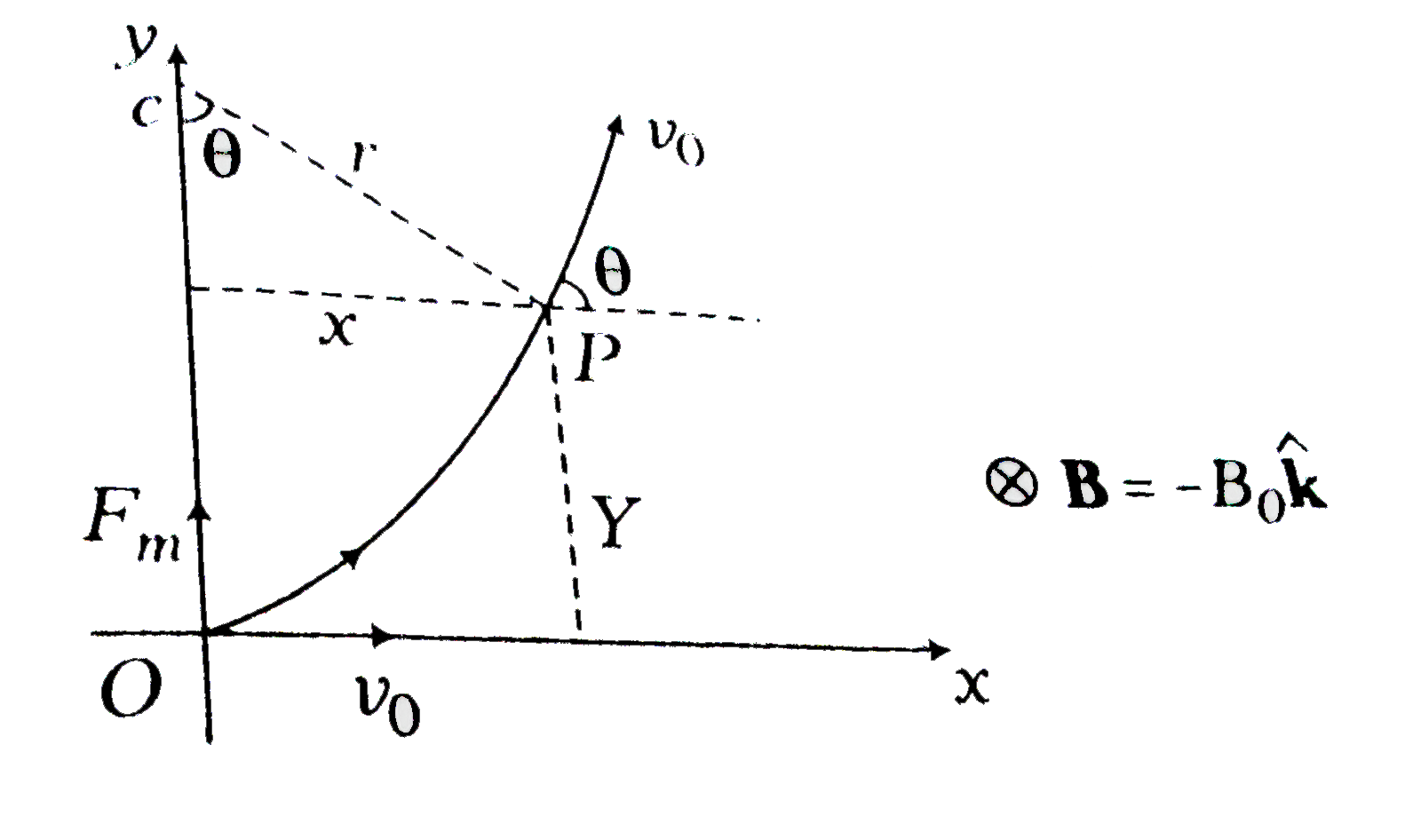
View SolutionA particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.

View SolutionA particle having mass m and charge q is released from the origin in a region in which ele field and magnetic field are given by B=−B0ˆjand E=E0ˆk.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.
View Solution
