According to classical physics, an electron in periodic motion with emit electromagnetic radiation with the same frequency as that of its revolution. Compute this value for hydrogen atom in nth quantum theory permit emission of such photons due to transition between adjoining orbits ? Discuss the result obtained.
To solve the problem, we need to compute the frequency of electromagnetic radiation emitted by an electron in a hydrogen atom during a transition between adjoining orbits, according to both classical and quantum theories. Let's break this down step by step.
Step 1: Frequency of Electron Revolution in Classical Physics
According to classical physics, an electron in a circular orbit emits electromagnetic radiation with a frequency equal to its orbital frequency. The frequency f of an electron in the n-th orbit can be derived from the formula:
f=me44πϵ20n3h2
Where:
- m is the mass of the electron,
- e is the charge of the electron,
- ϵ0 is the permittivity of free space,
- n is the principal quantum number (orbit number),
- h is Planck's constant.
This shows that the frequency is inversely proportional to n3:
f∝1n3
Step 2: Frequency of Emitted Radiation in Quantum Theory
In quantum theory, when an electron transitions from the n-th orbit to the (n−1)-th orbit, the frequency of the emitted radiation can be calculated using the energy difference between these two states:
f=En−En−1h
Using Bohr's model, the energy levels are given by:
En=−me48ϵ20h2n2
Thus, the energy difference is:
En−En−1=−me48ϵ20h2(1n2−1(n−1)2)
Calculating this difference gives:
En−En−1=−me48ϵ20h2((n−1)2−n2n2(n−1)2)=−me48ϵ20h2(−2n+1n2(n−1)2)
Substituting this into the frequency equation:
f=me48ϵ20h2⋅2n−1n2(n−1)2
Step 3: Comparing Classical and Quantum Frequencies
Now we compare the two frequencies:
1. Classical Frequency:
fclassical∝1n3
2. Quantum Frequency:
fquantum∝me48ϵ20h2⋅2n−1n2(n−1)2
Step 4: Discussion of Results
- For small values of n:
- The quantum frequency is significantly larger than the classical frequency due to the factor 2n−1 in the numerator of the quantum frequency expression. This indicates that the quantum model predicts a stronger emission of radiation during transitions between orbits.
- For large values of n:
- As n approaches infinity, the quantum frequency approaches the classical frequency, as the differences in energy levels become negligible. This is known as Bohr's correspondence principle, where quantum mechanics converges to classical mechanics in the limit of large quantum numbers.
Conclusion
The analysis shows that quantum mechanics provides a more accurate description of atomic transitions, especially at lower energy levels, while classical mechanics is a good approximation at higher energy levels.
- m is the mass of the electron,
- e is the charge of the electron,
- ϵ0 is the permittivity of free space,
- n is the principal quantum number (orbit number),
- h is Planck's constant.
fclassical∝1n3
fquantum∝me48ϵ20h2⋅2n−1n2(n−1)2
- The quantum frequency is significantly larger than the classical frequency due to the factor 2n−1 in the numerator of the quantum frequency expression. This indicates that the quantum model predicts a stronger emission of radiation during transitions between orbits.
- As n approaches infinity, the quantum frequency approaches the classical frequency, as the differences in energy levels become negligible. This is known as Bohr's correspondence principle, where quantum mechanics converges to classical mechanics in the limit of large quantum numbers.
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 4.2
12 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Subject
17 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Solved Examples
23 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
Similar Questions
According to classical electromagnetic theory, calculate the initial frequency of the light emitted by the electron revolving around a proton in hydrogen atom.
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
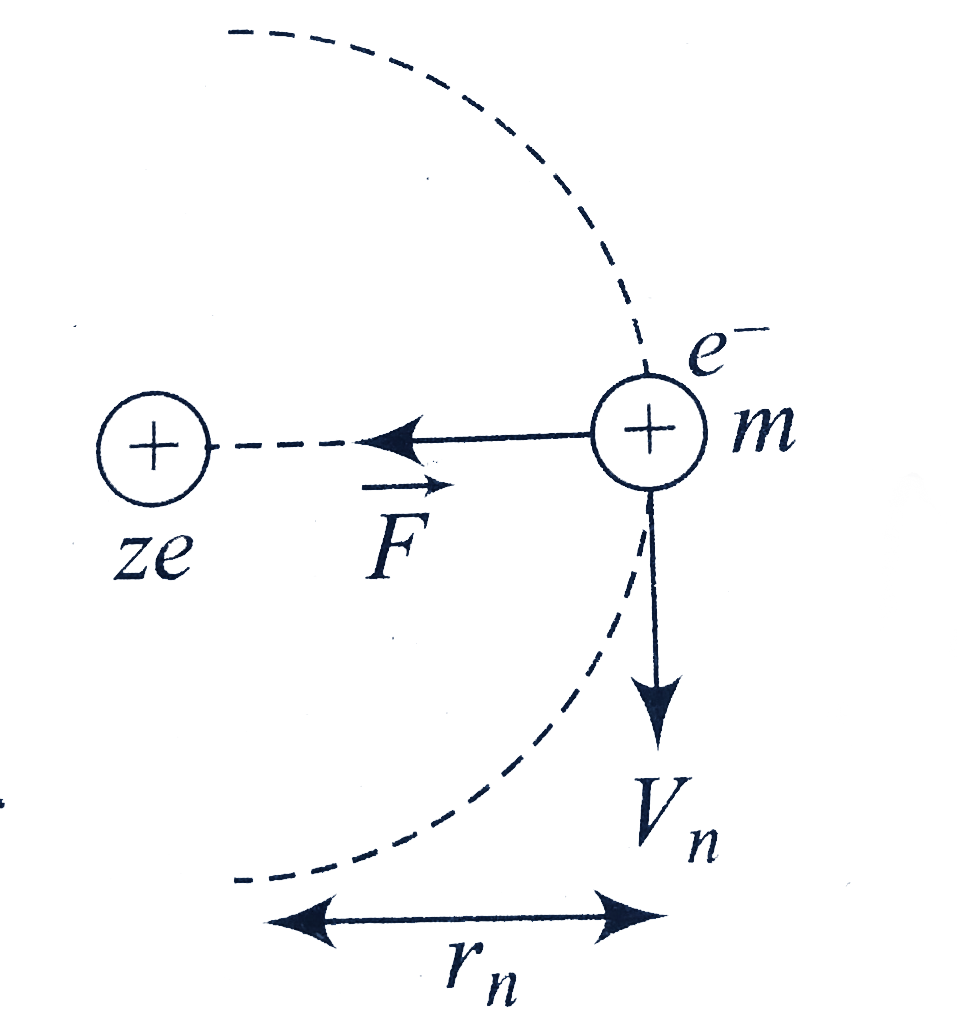
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state on the other planet should be
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
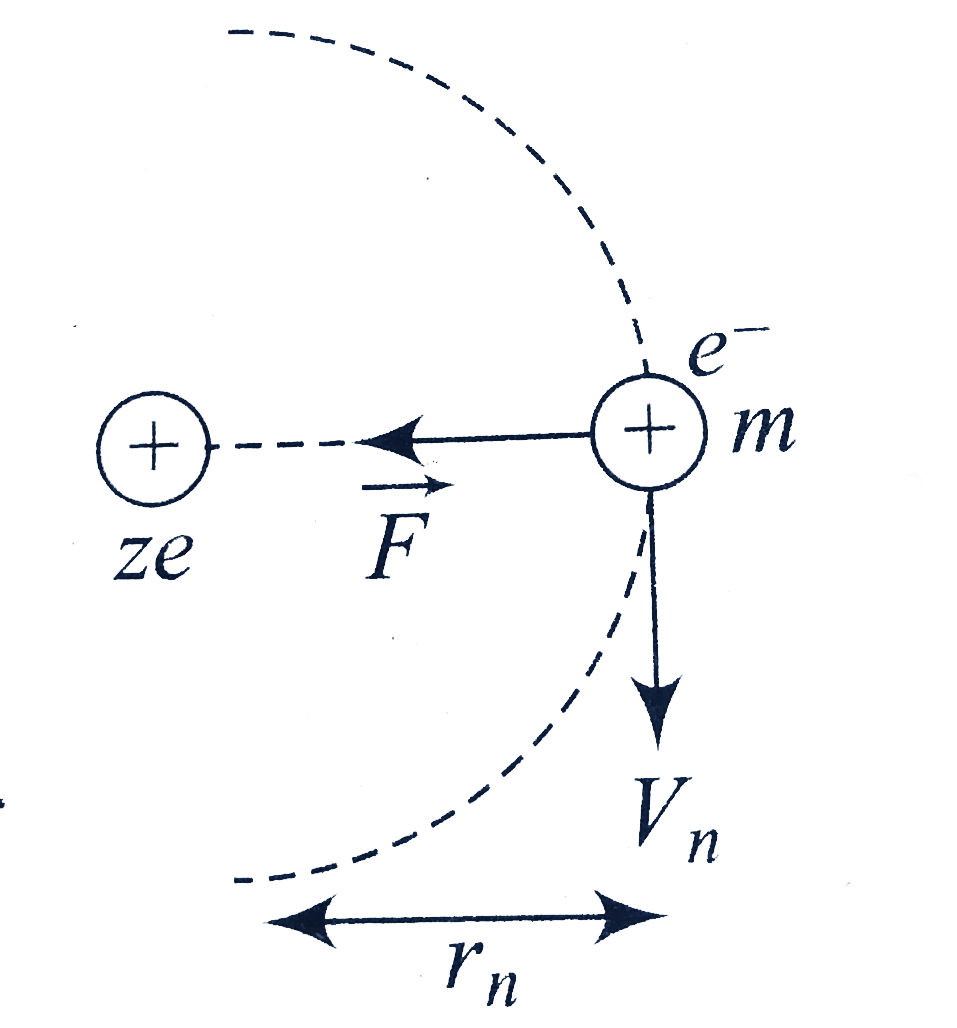
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planet, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multiple of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the ionization potential energy of a hydrogen atom is 13.6eV. On the other planet, this ionization potential energy will be
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
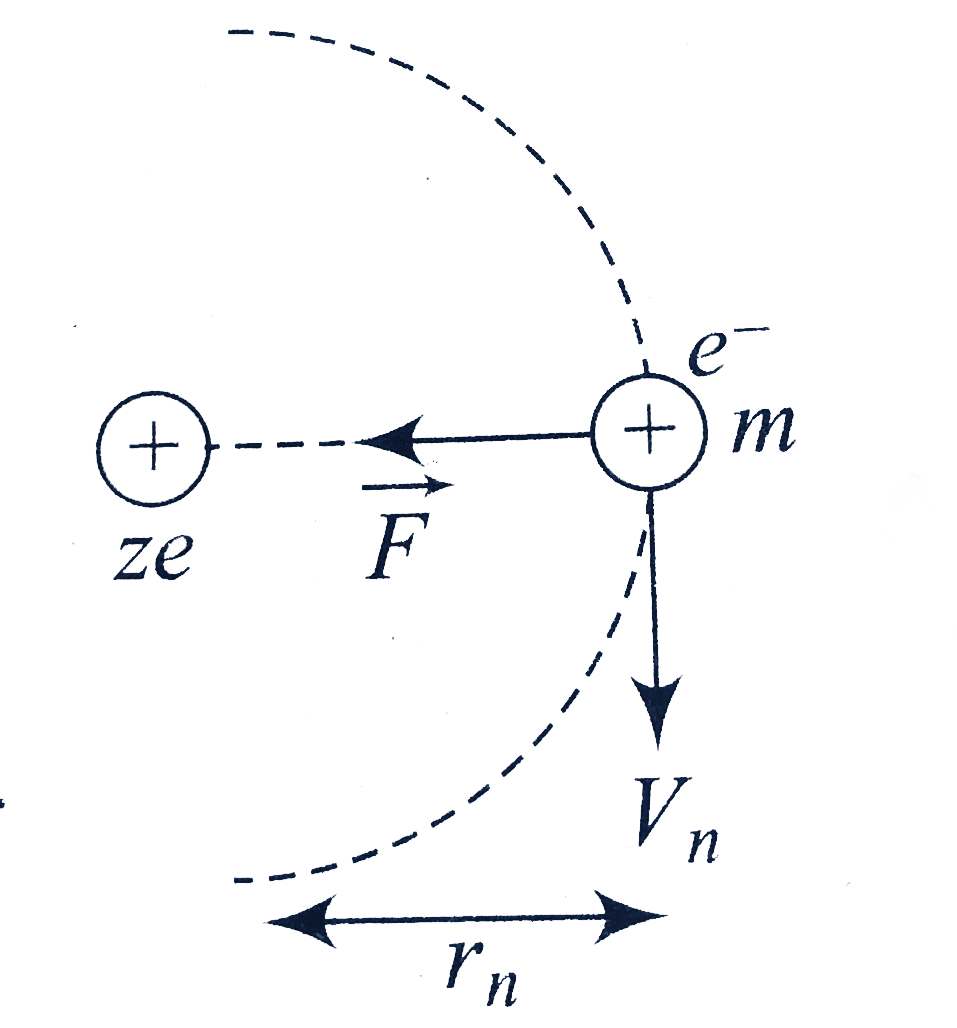
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
The minimum permissible radius of the orbit will be
View SolutionObtain an expression for the frequency of radiations emitted when a hydrogen atom de-excites from level n to level (n-1). for larger n, show that the frequency equals the classical frequency of revolution of the electron in the orbit.
View SolutionCalculate the ratio of the frequencies of the radiation emitted due to transition of the electron in a hydrogen atom from its (i) second permitted energy level to the first level and (ii) highest permitted energy level to the second permitted level .
View SolutionThe frequency of revolution of an electron in nth orbit is fn. If the electron makes a transition from nth orbit to (n=1) th orbit , then the relation between the frequency (v) of emitted photon and fn will be
View SolutionAccording to Bohr's theory, the time averaged magnetic field at the centre (i.e. nucleus) of a hydrogen atom due to the motion of electrons in the nth orbit is proportional to :
(n = principal quantum number)
View SolutionAccording to Bohr model, magnetic field at the centre (at the nucleus) of a hydrogen atom due to the motion of the electron in nth orbit is proportional to 1/nx, find the value of x
View SolutionA particle known as mu meson has a charge equal to that of no electron and mass 208times the mass of the electron B moves in a circular orbit around a nucleus of charge +3e Take the mass of the nucleus to be infinite Assuming that the bohr's model is applicable to this system (a)drive an expression for the radius of the nth Bohr orbit (b) find the value of a for which the radius of the orbit it appropriately the same as that at the first bohr for a hydrogen atom (c) find the wavelength of the radiation emitted when the u - mean jump from the orbit to the first orbit
View Solution
