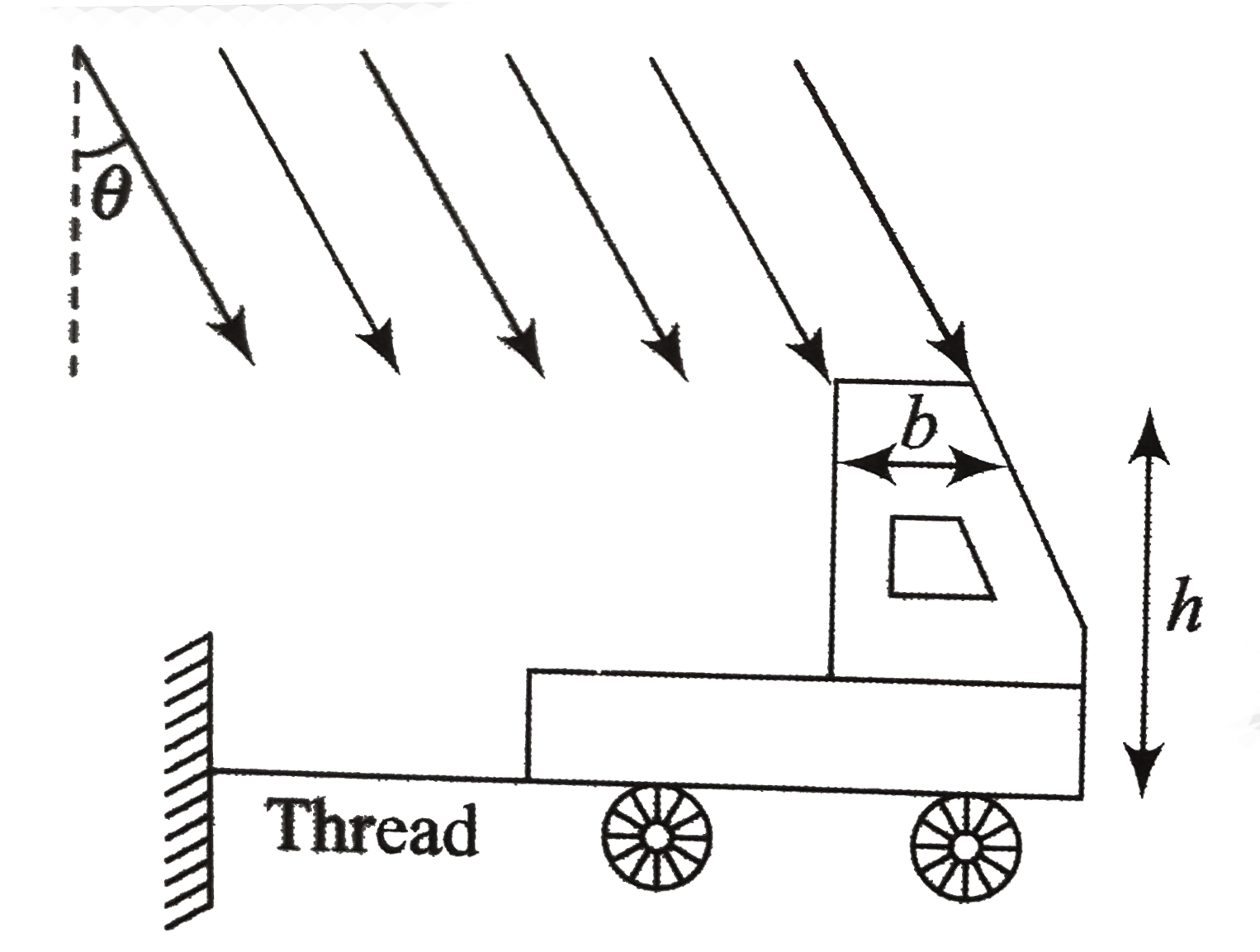
A toy truck has dimensions as shown in fig. and its width, normal to the plane of this paper, is d. The sun rays are incident on it as shiwn in the figure. If intensity of rays is I and all surfaces of truck are perfectly black, calculate tension in the thread used to keep the truck stationary. Neglect friction.

Video Solution

Text Solution

Verified by Experts

First, we have to calculate power incident on the truck and then momentum of light photons incident per second. Since the truck surfaces are perfectly black, therefore momentum finally reduces to zero. It means that the rate of change of momentum of light is equal to the momentum of photons incident per second.
Area of top of the driving cabin $= b d$ .
Light is incident due to the component I $cos θ$ of intensity I.
Power incident on top of the cabin $= b d I cos θ$
Similarly, power incident on rear horizontal part of the truck is $a d I cos θ$ and power incident on rear vertical wall of the driving cabin in $h d I sin θ$ .
Total power incident on the truck is
$P = (b cos θ + a cos θ + h sin θ) I d$
Momentum of these photons is $p = \frac{P}{c}$ (where c is speed of light in vacuum).
But rate of change in momentum of photons,
$p = (\frac{I d}{c}) (b cos θ + a cos θ + h sin θ)$
This momentum is inclined at angle $θ$ with vertical. Its vertical component $p cos θ$ is balanced by normal reaction of the floor and horizontal component $ψ n θ$ is balanced by tension in the thread.
Tension $= p sin θ = (\frac{I d}{c} (b cos θ + a cos θ + h sin θ) sin θ)$

Updated on:21/07/2023

|

Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER

Topper's Solved these Questions

CENGAGE PHYSICS ENGLISH-PHOTOELECTRIC EFFECT-Integer Type

Home
Ask Doubt
Profile