Most materials have the refractive index, n>1. So, when a light ray from air enters a naturally occuring material, then by Snell's law, sinθ1sinθ2=n1n2, it is understood that the refracted ray bends towards the normal. But it never emerges on the same side of the normal as the incident ray. According to electromagnetism, the refractive index of the medium is given by the relation, n=(c/v)=±√εr,μr, where c is the speed of the electromagnetic waves in vacuum, v its speed in the medium, εr and μr are negative, one must choose the negative root of n. Such negative refractive index materials can now be artifically prepared and are called meta-materials. They exhibit significantly different optical behaviour, without violating any physical laws. Since n is negative, it results in a change in the direction of propagation of the refracted light. However, similar to normal materials, the frequency of light remains unchanged upon refraction even in meta-materials.
Answer the following questions :
For light incident from air on a meta-material, the appropriate ray diagram is
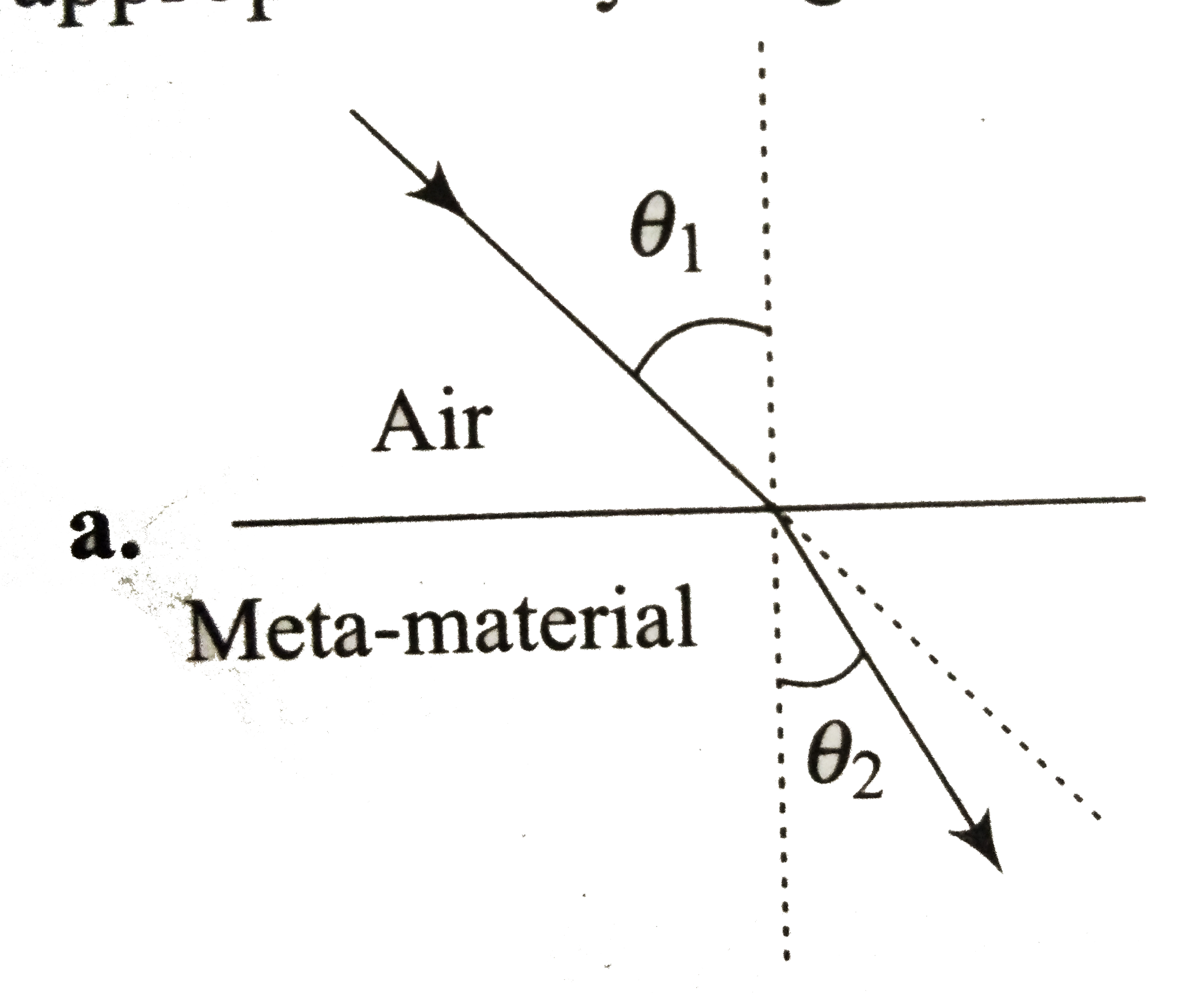

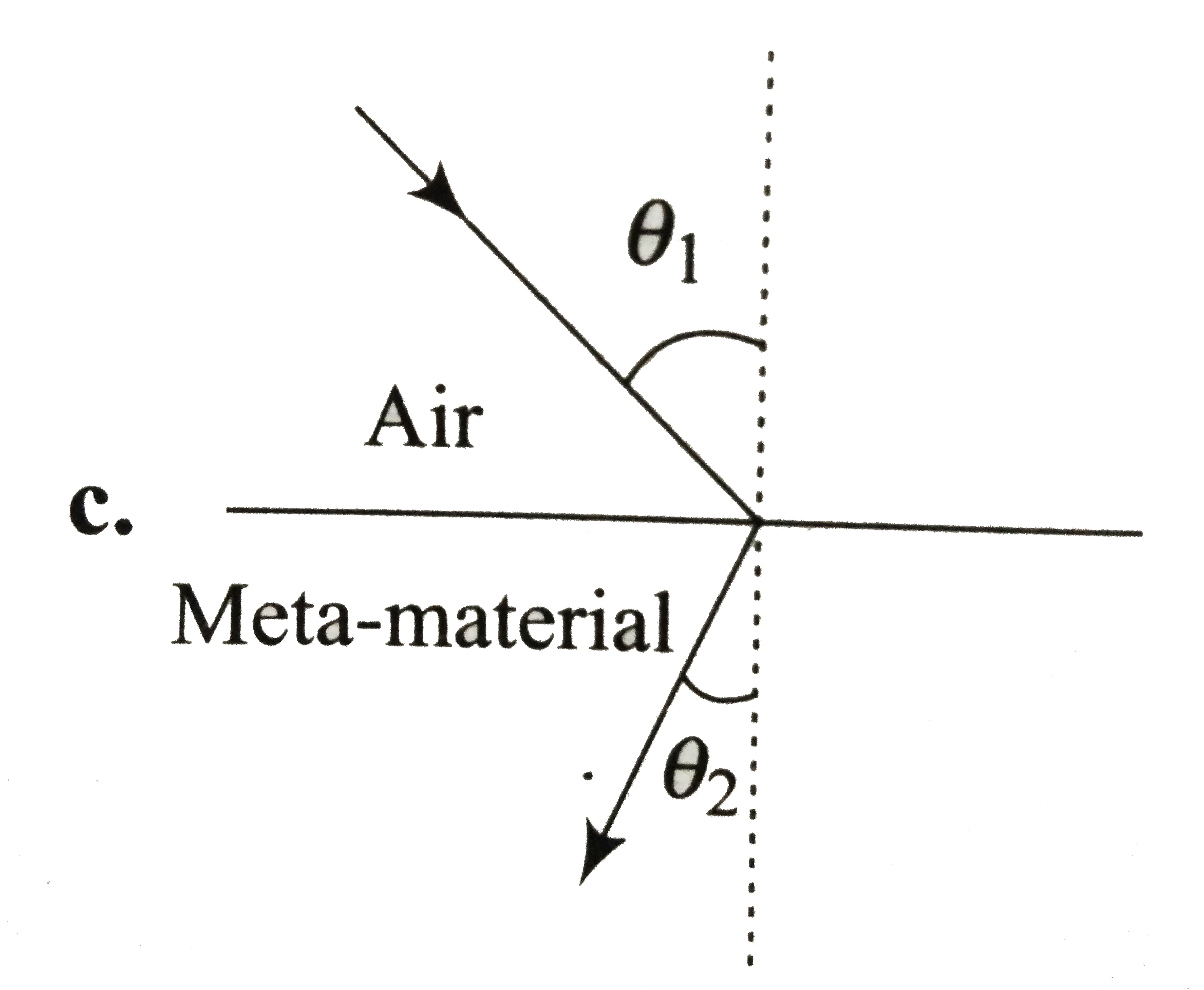

The correct Answer is:c
To solve the problem of determining the direction of the refracted ray when light passes from air into a metamaterial with a negative refractive index, we can follow these steps:
Step 1: Understand Snell's Law
Snell's law states that:
sinθ1sinθ2=n1n2
where:
- θ1 is the angle of incidence,
- θ2 is the angle of refraction,
- n1 is the refractive index of the first medium (air, which is approximately 1),
- n2 is the refractive index of the second medium (metamaterial, which is negative).
Step 2: Substitute Values
Since the refractive index of air n1=1 and the refractive index of the metamaterial n2<0, we can rewrite Snell's law:
sinθ2=n1sinθ1n2=sinθ1n2
Since n2 is negative, this means:
sinθ2=sinθ1n2<0
This implies that θ2 must be negative.
Step 3: Analyze the Implications
A negative angle for θ2 indicates that the refracted ray is bending away from the normal. In typical scenarios where n2>1, the light bends towards the normal, but in this case, since n2 is negative, the light will bend in the opposite direction.
Step 4: Draw the Ray Diagram
1. Draw the boundary between air and the metamaterial.
2. Draw the incident ray coming from air at an angle θ1 towards the boundary.
3. Since θ2 is negative, draw the refracted ray on the opposite side of the normal, indicating that it is bending away from the normal.
Step 5: Identify the Correct Ray Diagram
From the options provided, the correct ray diagram will show the refracted ray bending away from the normal, indicating that it is in the opposite direction compared to the incident ray.
Conclusion
The correct option for the ray diagram is the one that shows the refracted ray bending away from the normal.
---
Snell's law states that:
sinθ1sinθ2=n1n2
where:
- θ1 is the angle of incidence,
- θ2 is the angle of refraction,
- n1 is the refractive index of the first medium (air, which is approximately 1),
- n2 is the refractive index of the second medium (metamaterial, which is negative).
Since the refractive index of air n1=1 and the refractive index of the metamaterial n2<0, we can rewrite Snell's law:
sinθ2=n1sinθ1n2=sinθ1n2
Since n2 is negative, this means:
sinθ2=sinθ1n2<0
This implies that θ2 must be negative.
A negative angle for θ2 indicates that the refracted ray is bending away from the normal. In typical scenarios where n2>1, the light bends towards the normal, but in this case, since n2 is negative, the light will bend in the opposite direction.
1. Draw the boundary between air and the metamaterial.
2. Draw the incident ray coming from air at an angle θ1 towards the boundary.
3. Since θ2 is negative, draw the refracted ray on the opposite side of the normal, indicating that it is bending away from the normal.
From the options provided, the correct ray diagram will show the refracted ray bending away from the normal, indicating that it is in the opposite direction compared to the incident ray.
The correct option for the ray diagram is the one that shows the refracted ray bending away from the normal.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Matching Column Type
2 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - MCQ
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
Most materials have the refractive index, n>1. So, when a light ray from air enters a naturally occuring material, then by Snell's law, sinθ1sinθ2=n1n2, it is understood that the refracted ray bends towards the normal. But it never emerges on the same side of the normal as the incident ray. According to electromagnetism, the refractive index of the medium is given by the relation, n=(c/v)=±√εr,μr, where c is the speed of the electromagnetic waves in vacuum, v its speed in the medium, εr and μr are negative, one must choose the negative root of n. Such negative refractive index materials can now be artifically prepared and are called meta-materials. They exhibit significantly different optical behaviour, without violating any physical laws. Since n is negative, it results in a change in the direction of propagation of the refracted light. However, similar to normal materials, the frequency of light remains unchanged upon refraction even in meta-materials.
Answer the following questions :
Choose the correct statement.
View SolutionOne of the refracting surfaces of a prism of angle of 30∘ is silvered. A ray of light incident at an angle of 60∘ retraces its path. The refractive index of the material of prism is
View SolutionA ray of light incidents on a refracting surface at 30∘ with the surface . If the angle of refraction is 45∘ refractive index of the medium is
View SolutionWhen light rays enter the eye, most of the refraction occurs at the
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5)
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View SolutionThe angle of minimum deviation for an incident ligt ray on an equillateral prism is equal to its refracting angle. The refractive index of its material is
View SolutionWhen light travels from glass to air, the incident angle is θ1 and the refracted angle is θ2. The true relation is
View SolutionA light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View SolutionThe incident ray, the _______ ray and the normal lie in the same plane during refraction.
View Solution
