Microwaves from a transmitter are directed normally toward a plane reflector. A detector moves along the normal to the reflector. Between positions of 14 successive maxima the detector travels a distance 0.14 m. The frequency of the transmitter is (c=3×108ms−1).
1.5×1010Hz
3.0×1010Hz
1.5×109Hz
3.0×109Hz
The correct Answer is:a
To solve the problem, we need to determine the frequency of the microwaves emitted by the transmitter. Here’s a step-by-step breakdown of the solution:
Step 1: Understanding the Problem
The detector moves along the normal to the reflector and detects maxima due to the interference of direct and reflected microwaves. The distance traveled by the detector between 14 successive maxima is given as 0.14 m.
Step 2: Relating Distance to Wavelength
The distance between two successive maxima in an interference pattern is equal to half the wavelength (λ/2). Therefore, if the detector travels a distance of 0.14 m for 14 maxima, we can express this mathematically.
Step 3: Setting Up the Equation
Since there are 14 maxima, the number of half wavelengths (λ/2) that fit into the distance of 0.14 m is 14. Thus, we can write:
14×λ2=0.14 m
Step 4: Solving for Wavelength (λ)
Now, we can solve for λ:
14λ2=0.14
7λ=0.14
λ=0.147=0.02 m
Step 5: Using the Wave Equation
We know the relationship between the speed of light (c), frequency (n), and wavelength (λ) is given by:
c=nλ
where:
- c=3×108 m/s
- λ=0.02 m
Step 6: Solving for Frequency (n)
Rearranging the equation to solve for frequency (n):
n=cλ
Substituting the known values:
n=3×1080.02
Calculating this gives:
n=3×108÷0.02=1.5×1010 Hz
Final Answer
The frequency of the transmitter is:
n=1.5×1010 Hz
The detector moves along the normal to the reflector and detects maxima due to the interference of direct and reflected microwaves. The distance traveled by the detector between 14 successive maxima is given as 0.14 m.
The distance between two successive maxima in an interference pattern is equal to half the wavelength (λ/2). Therefore, if the detector travels a distance of 0.14 m for 14 maxima, we can express this mathematically.
Since there are 14 maxima, the number of half wavelengths (λ/2) that fit into the distance of 0.14 m is 14. Thus, we can write:
14×λ2=0.14 m
Now, we can solve for λ:
14λ2=0.14
7λ=0.14
λ=0.147=0.02 m
We know the relationship between the speed of light (c), frequency (n), and wavelength (λ) is given by:
c=nλ
where:
- c=3×108 m/s
- λ=0.02 m
Rearranging the equation to solve for frequency (n):
n=cλ
Substituting the known values:
n=3×1080.02
Calculating this gives:
n=3×108÷0.02=1.5×1010 Hz
The frequency of the transmitter is:
n=1.5×1010 Hz
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
Plane microwaves from a transmitter are directed normally towards a plane reflector. A detector moves along the normal to the reflection. Between positions of 14 successive maxima, the detector travels a distance 0.14m. If the velocity of light is 3×108m/s, find the frequency of the transmitter.
View SolutionA boat is travelling in a river with a speed 10m/s along with stream flowing 2m/s. From this boat, a sound transmitter is lowered into the river through a rigid support. The wavelength of the sound emitted from the transmitter inside the water is 14.45mm. Assume that attenuation of sound in water and air is negligible.
(a) What will be the frequency detected by a receiver kept inside the river downstream?
(b) The transmitter and the receiver are now pulled up into air. the air is blowing with a speed 5m/s in the direction opposite the river stream. Determine the frequency of the sound detected by the receiver.
(Temperature of the air and water = 20∘C, Density of river water =103kg/m3,
Bulk modulus of the water =2.088×109Pa, gas constant R=8.31J/mol−K,
Mean molecular mass of air =28.8×10−3kg/mol, CP/CV for air =1.4)
View SolutionA detector is released from rest over a source of sound of frequency f0=103Hz. The frequency observed by the detector at time t is plotted in the graph. The speed of sound in air is (g=10m/s2)
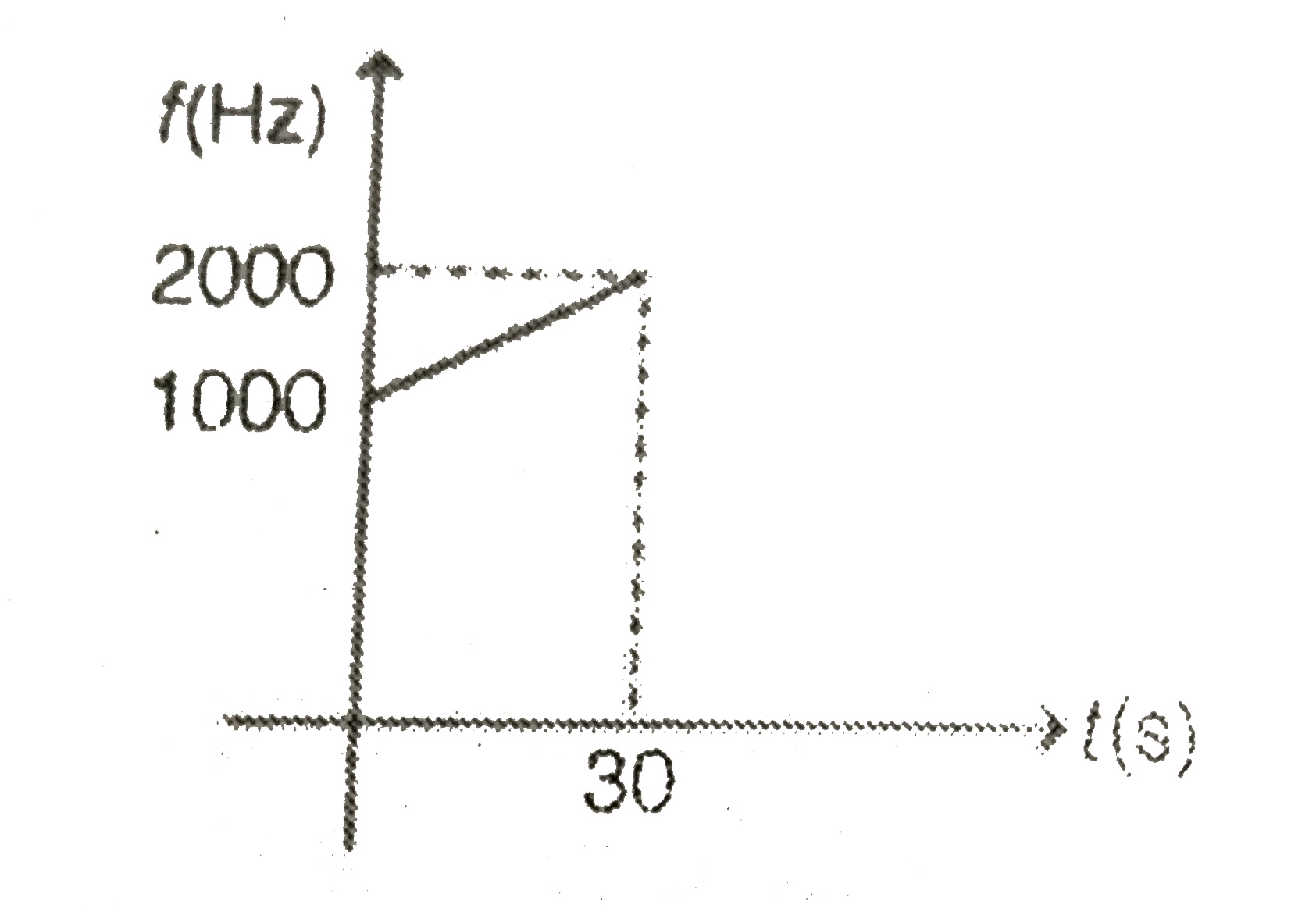
View SolutionA boat is travelling in a river with a speed 10m/s along the stream flowing with a speed 2m/s . From this boat , a sound transmitter is lowered into the river throught a rigid support. The wavelength of the sound emitted from the transmitter inside the water is 14.45mm . Aassume that attenuation of sound in water and air is neglisible.
(a) What will be the frequency delected by a receiver kept inside the river downstream ?
(b) The transmitter and the reciver are now pulled up into air. The air is blowing with a speed 5m/s in the direction opposite the river stream. Determine the frequency of the sound delected by the reciver.
(Temperature of the air and water = 20∘C , Density of river water = 103kg/m3 , Bulk modulus of the water = 2.088×109Pa , Gas constant, R=8.31J/mol−K , Mean molecular mass of air = 28.8×10−3kg/mol , Cp/CV for air = 1.4
View SolutionMicrowaves are reflected from a distant airplane approaching a stationary observer. It is found that when the reflected waves beat against the waves radiating from the source, the beat frequency is 900 Hz. Calculate the approach speed of the airplane if the wavelength of the microwave is 0.1 H. Velocity of microwave is 3×108 m/s.
View SolutionA flat plate moves normally towards a discharging jet of water at the rate of 3m/s. The jet discharges the water at the rate of 0.1m3/s and at the speed of 18m/s. The force exerted on the plate due to the jet is
View SolutionWhen the resistance of copper wire is 0.1Ω and the radius is 1mm, then the length of the wire is (specific resistance of copper is 3.14×10−8ohm×m)
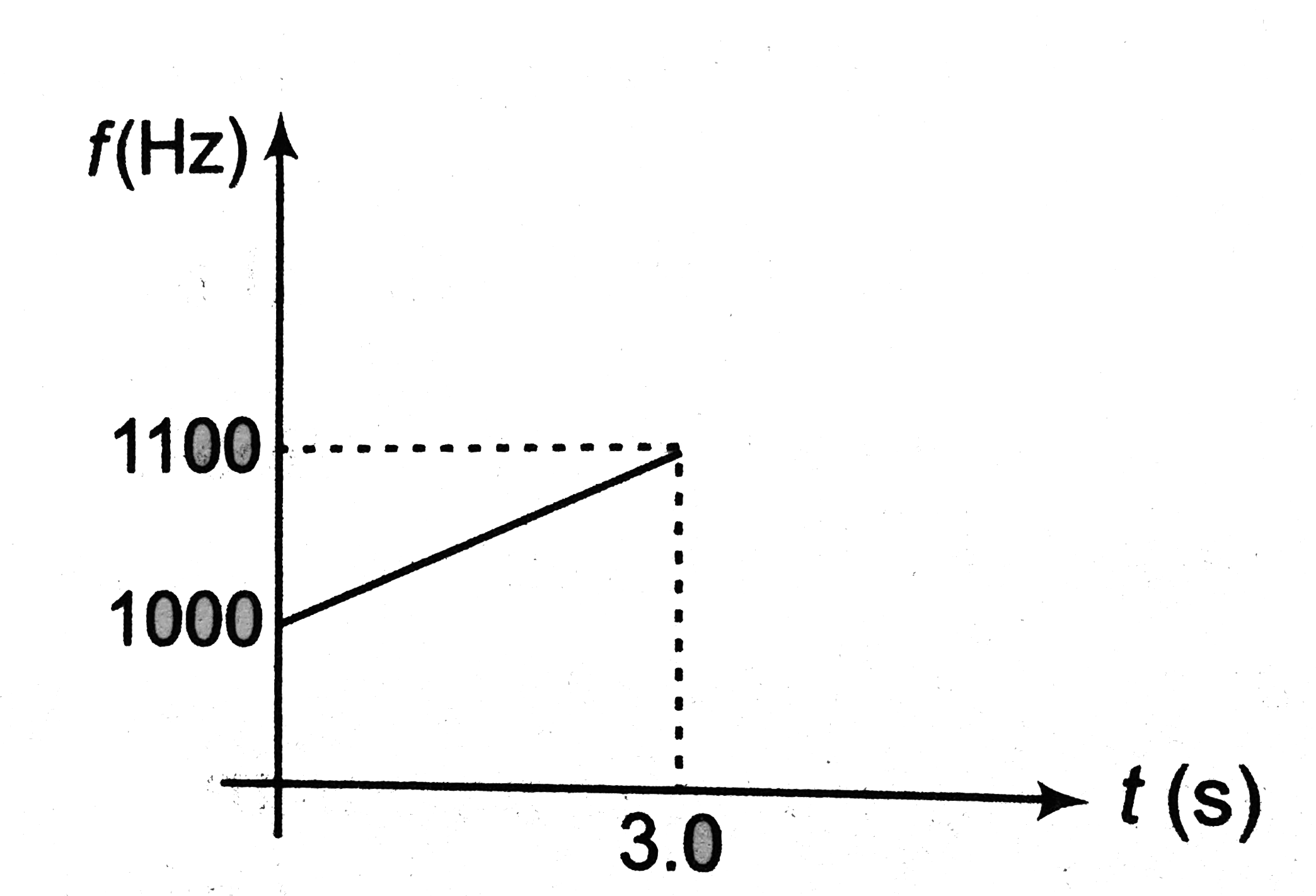
View SolutionA detector is released from rest over a source of sound of frequency fo=103HZ. The frequency observer by the decector at time t is plotted in the graph. The speed of sound in air (g=10m/s2)
View SolutionDuring an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station ? The signal travels at the speed of light, that is, 3×108m/s.
View Solution
A source of sound and a detector are placed at the same place on ground At t=0, the source S is projected towards reflector with velocity v0 in vertical upward directon and reflector starts moving down with constant velocity v0 At t=0, the vertical separation between the reflector and source is H(>v202g). The speed of sound in air is v(>>v0), Take f0 as the frequency of sound waves emitted by source. Based on above information answer the following questions.
Q. Frequency of sound received by detector after being reflected by reflector at t=v02g is
View Solution
