A container of uniform cross-section has a height of 14 m. Upto what height (in metre) water of refractive index 4/3 should be filled for normal viewing.
The correct Answer is:8
To solve the problem of determining the height to which water should be filled in a container for normal viewing, we can follow these steps:
1. Understand the Problem:
- We have a container with a uniform cross-section and a total height of 14 meters.
- We need to find the height h of water that should be filled in the container, given that the refractive index of water is 43.
2. Set Up the Relationship:
- When viewing from the top of the container, the apparent depth of the water is less than the actual depth due to refraction.
- The relationship between the actual depth h and the apparent depth can be expressed as:
Apparent Depth=hμ
- Here, μ is the refractive index of water, which is 43.
3. Determine the Apparent Depth:
- The apparent depth when viewed from the top is given by:
Apparent Depth=14−h
- This means that the apparent depth is the total height of the container minus the height of the water.
4. Set Up the Equation:
- From the relationships established, we can equate the two expressions for apparent depth:
h43=14−h
5. Clear the Fraction:
- To eliminate the fraction, multiply both sides of the equation by 43:
h=43(14−h)
6. Distribute and Rearrange:
- Distributing 43:
h=563−43h
- Rearranging gives:
h+43h=563
- This simplifies to:
73h=563
7. Solve for h:
- Multiply both sides by 37:
h=567=8
8. Conclusion:
- The height of water that should be filled in the container for normal viewing is h=8 meters.
Final Answer:
The height of water that should be filled in the container is 8 meters.
- We have a container with a uniform cross-section and a total height of 14 meters.
- We need to find the height h of water that should be filled in the container, given that the refractive index of water is 43.
- When viewing from the top of the container, the apparent depth of the water is less than the actual depth due to refraction.
- The relationship between the actual depth h and the apparent depth can be expressed as:
Apparent Depth=hμ
- Here, μ is the refractive index of water, which is 43.
- The apparent depth when viewed from the top is given by:
Apparent Depth=14−h
- This means that the apparent depth is the total height of the container minus the height of the water.
- From the relationships established, we can equate the two expressions for apparent depth:
h43=14−h
- To eliminate the fraction, multiply both sides of the equation by 43:
h=43(14−h)
- Distributing 43:
h=563−43h
- Rearranging gives:
h+43h=563
- This simplifies to:
73h=563
- Multiply both sides by 37:
h=567=8
- The height of water that should be filled in the container for normal viewing is h=8 meters.
The height of water that should be filled in the container is 8 meters.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives
7 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - True/False
5 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A vertical U-tube of uniform cross-section contains water upto a height to 0.8 m. Show. that if the water on one side is depressed and then released, its motion up and down the tube is shm. Calculate the period.
View SolutionA vertical U-tube of uniform cross-section contains water upto a height of 30 cm. show that if the water in one limb is depressed and then released, its up and down motion in the two limbs of the tube is simple harmonic and calculate its time-period.
View SolutionIn figure, a point source S is placed at a height h above the plane mirror in a medium of refractive index μ.
a. Find the number of images seen for normal view.
b. Find the distance between the images.

View SolutionA container of cross-section area 'S' and height 'h' is filled with mercury up to the brim. Then the container is sealed airtight and a hole of small cross section area 'S/n' (where 'n' is a positive constant) is puched in its bottom. Find out the time interval upto which the mercury will come out from the bottom hole.
[Take the atmospheric pressure to be equal to h0 height of mercury column: h>h0]
View SolutionA vesserl contains a slab of glass 8cm thick and of refractive index 1.6 . Over the slab, the vessel is filled by oil of refractive index μ upto height 4.5 cm and then by another liquid, i.e., water of refractive index 4/3 and height 6cm as shown in Figure. An observer looking down from above observer that a mark at the bottom of glass slab appears to be raised up to a position 6cm from bottom of the slab. Find refractive index of oil (μ) .

View SolutionA piece of wood of uniform cross section and height 15 cm floats vertically with its height 10 cm in water and 12 cm in spirit. Find the density of (i) wood and (ii) spirit
View SolutionA tank of base area 4m2 is initially filled with water up to height 2m. An object of uniform cross-section 2m2 and height 1m is now suspended by wire into the tank, keeping distance between base of tank and that of object 1m. Density of the object is 2000kg/m3. Take atmospheric pressure 1×105N/m2,g=10m/s2.
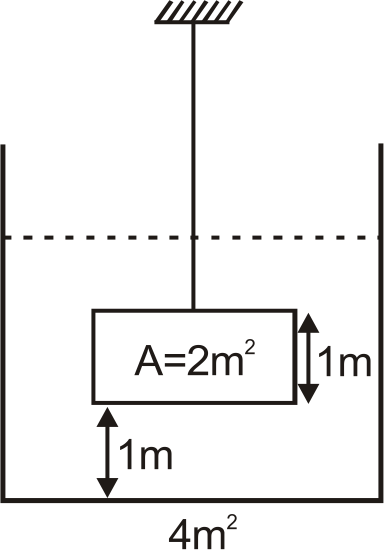
The downwards force exerted by the water on the top surface of the object is
View SolutionA tank of base area 4m2 is initially filled with water up to height 2m. An object of uniform cross-section 2m2 and height 1m is now suspended by wire into the tank, keeping distance between base of tank and that of object 1m. Density of the object is 2000kg/m3. Take atmospheric pressure 1×105N/m2,g=10m/s2.
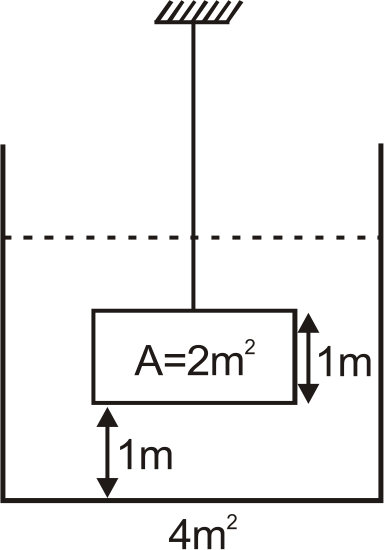
The tension in the wire is
View SolutionA tank of base area 4m2 is initially filled with water up to height 2m. An object of uniform cross-section 2m2 and height 1m is now suspended by wire into the tank, keeping distance between base of tank and that of object 1m. Density of the object is 2000kg/m3. Take atmospheric pressure 1×105N/m2,g=10m/s2.
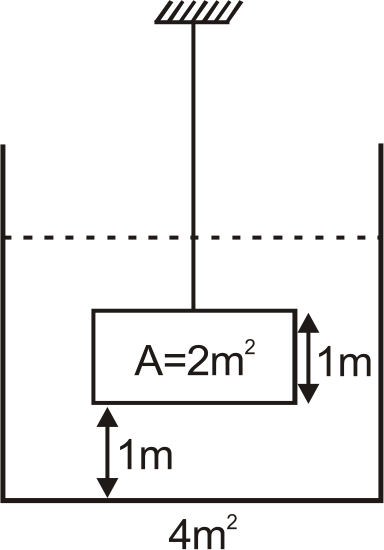
The buyont force on the object is
View SolutionTwo liquid columns of same height 5m and densities ρ and 2ρ are filled in a container of uniform cross sectional area. Then ratio of force exerted by the liquid on upper half of the wall to lower half of the wall is.
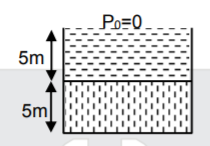
View Solution
