A convex lens of focal length 20cm and a concave lens of focal length f are mounted coaxially 5cm apart. Parallel beam of light incident on the convex lens emerges from the concave lens as a parallel beam. Then, f in cm is
35
25
20
15
The correct Answer is:d.
To solve the problem, we need to find the focal length f of the concave lens such that a parallel beam of light incident on the convex lens emerges as a parallel beam after passing through the concave lens.
1. Identify the Focal Lengths:
- The focal length of the convex lens f1=+20 cm (positive because it is a converging lens).
- The focal length of the concave lens f2=f (we need to find this value).
2. Understand the Configuration:
- The convex lens and concave lens are placed 5 cm apart.
- A parallel beam of light entering the convex lens will converge to a point after passing through it.
3. Condition for Parallel Emergence:
- For the light to emerge as a parallel beam after passing through the concave lens, the effective focal length of the combined lens system must be infinite. This means that the rays should not converge or diverge after passing through both lenses.
4. Use the Lens Formula:
- The formula for two lenses in contact (or coaxially aligned) is given by:
1F=1f1+1f2−df1f2
where d is the distance between the two lenses (5 cm in this case).
5. Set the Effective Focal Length to Infinity:
- Since the final focal length F must be infinite, we set:
1F=0
Therefore, we have:
0=120+1f−520f
6. Rearranging the Equation:
- Rearranging gives:
1f−520f=−120
- Simplifying the left side:
1f−14f=−120
- Combine the fractions:
4−14f=−120
34f=−120
7. Cross-Multiplying:
- Cross-multiplying gives:
3⋅20=−4f
60=−4f
- Solving for f:
f=−604=−15 cm
8. Final Answer:
- The focal length of the concave lens is f=−15 cm. The magnitude is 15 cm, and since it is a concave lens, it is negative.
Summary:
The focal length f of the concave lens is −15 cm.
- The focal length of the convex lens f1=+20 cm (positive because it is a converging lens).
- The focal length of the concave lens f2=f (we need to find this value).
- The convex lens and concave lens are placed 5 cm apart.
- A parallel beam of light entering the convex lens will converge to a point after passing through it.
- For the light to emerge as a parallel beam after passing through the concave lens, the effective focal length of the combined lens system must be infinite. This means that the rays should not converge or diverge after passing through both lenses.
- The formula for two lenses in contact (or coaxially aligned) is given by:
1F=1f1+1f2−df1f2
where d is the distance between the two lenses (5 cm in this case).
- Since the final focal length F must be infinite, we set:
1F=0
Therefore, we have:
0=120+1f−520f
- Rearranging gives:
1f−520f=−120
- Simplifying the left side:
1f−14f=−120
- Combine the fractions:
4−14f=−120
34f=−120
- Cross-multiplying gives:
3⋅20=−4f
60=−4f
- Solving for f:
f=−604=−15 cm
- The focal length of the concave lens is f=−15 cm. The magnitude is 15 cm, and since it is a concave lens, it is negative.
The focal length f of the concave lens is −15 cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A convex lens of focal length 1.0m and a concave lens of focal length 0.25m are 0.75m apart. A parallel beam of light is incident on the convex lens. The beam emerging after refraction from both lenses is
View SolutionA convex lens of focal length 100 cm and a concave lens of focal length 10 cm are placed coaxialiy at a separation of 90 cm. If a parallel beam of light is incident on convex lens, then after passing through the two lenses the beam
View SolutionA convex lens of focal length A and a concave lens of focal length B are placed in contact. The focal length of the combination is
View SolutionA convex lens of focal length 80 cm and a concave lens of focal length 50 cm are combined toghether. What will be their resulting power ?
View SolutionA convex lens of focal length 1 meter and a concave lens fo focal length 0.25 meter and kept 0.75 meter apart. A parallel beam of light first passes through the ocnvex lens, then through the concave lens and comes to a focus 0.5m away from the concave lens.
View SolutionA convex lens A of focal length 20cm and a concave lens B of focal length 5cm are kept along the same axis with a distance d between them. I a parallel lbeam of leight falling on A leaved B as a parallel beam, then d is equal to ____________cm.
View SolutionA convex lens A of focal length 20cm and a concave lens G of focal length 5cm are kept along the same axis with the distance d between them. If a parallel beam of light falling on A leaves B as a parallel beam, then distance d in cm will be
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View SolutionA thin convex lens (L1) of focal length 80 cm and a thin concave lens (L2) of focal length f are kept co-axially, 20 cm apart as shown in figure below. When a narrow and parallel beam of light is incident on the conver lens, beam emerging from the concave lens is also a parallel beam. Find f.
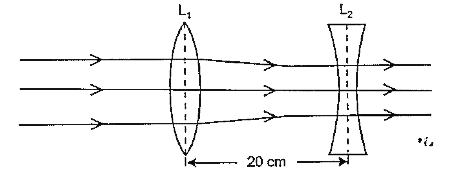
View SolutionA convex lens of focal length 20 cm and a concave lens of focal length 10 cm are placed 20 cm apart. In between them an object placed at distance x from the convex lens.
What is the value of x (in cm ) so that images from by both the lenses coincides ?
View Solution
