Statement I: When an external resistor of resistance R (connected across a cell to internal resistance r ) is varied, power consumed by resistance R is maximum when R = r.
Statement II: Power consumed by a resistor of constant resistance R is maximum when current through it is maximum.
Statement I is true, Statement II is True, Statement II is a correct explanation for Statement I.
Statement I is True, Statement II is True, Statement II is not a correct explanation for Statement I.
Statement I is True, Statement II is False.
Statement I is False, Statement II is True.
The correct Answer is:B
To solve the problem, we need to analyze both statements and determine their validity based on the principles of electrical circuits.
Step 1: Analyze Statement I
- Statement I claims that the power consumed by an external resistor R connected across a cell with internal resistance r is maximum when R=r.
- The total current I flowing through the circuit can be expressed as:
I=ER+r
where E is the electromotive force (emf) of the cell.
Step 2: Calculate Power across the External Resistor
- The power P consumed by the external resistor R can be given by:
P=I2R=(ER+r)2R
Simplifying this, we get:
P=E2R(R+r)2
Step 3: Find Maximum Power Condition
- To find the condition for maximum power, we differentiate P with respect to R and set the derivative to zero:
dPdR=0
- Using the quotient rule for differentiation, we can differentiate P:
dPdR=(R+r)2⋅E2−E2R⋅2(R+r)(R+r)4
Setting the numerator to zero gives:
(R+r)2−2R(R+r)=0
Simplifying this leads to:
R+r−2R=0⟹r=R
- This shows that the power is maximum when R=r. Thus, Statement I is correct.
Step 4: Analyze Statement II
- Statement II states that the power consumed by a resistor of constant resistance R is maximum when the current through it is maximum.
- The power P across a resistor is given by:
P=I2R
- Since R is constant, P is directly proportional to I2. Therefore, if the current I is maximum, the power P will also be maximum. Hence, Statement II is also correct.
Step 5: Conclusion
- Both statements are correct, but Statement II does not explain Statement I. Therefore, the answer is that Statement I is correct and Statement II is also correct but does not explain Statement I.
Final Answer:
- Statement I is correct.
- Statement II is correct but does not explain Statement I.
---
- Statement I claims that the power consumed by an external resistor R connected across a cell with internal resistance r is maximum when R=r.
- The total current I flowing through the circuit can be expressed as:
I=ER+r
where E is the electromotive force (emf) of the cell.
- The power P consumed by the external resistor R can be given by:
P=I2R=(ER+r)2R
Simplifying this, we get:
P=E2R(R+r)2
- To find the condition for maximum power, we differentiate P with respect to R and set the derivative to zero:
dPdR=0
- Using the quotient rule for differentiation, we can differentiate P:
dPdR=(R+r)2⋅E2−E2R⋅2(R+r)(R+r)4
Setting the numerator to zero gives:
(R+r)2−2R(R+r)=0
Simplifying this leads to:
R+r−2R=0⟹r=R
- This shows that the power is maximum when R=r. Thus, Statement I is correct.
- Statement II states that the power consumed by a resistor of constant resistance R is maximum when the current through it is maximum.
- The power P across a resistor is given by:
P=I2R
- Since R is constant, P is directly proportional to I2. Therefore, if the current I is maximum, the power P will also be maximum. Hence, Statement II is also correct.
- Both statements are correct, but Statement II does not explain Statement I. Therefore, the answer is that Statement I is correct and Statement II is also correct but does not explain Statement I.
- Statement I is correct.
- Statement II is correct but does not explain Statement I.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:Integer Answer Type
Explore 11 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:True and False
Explore 3 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:Multiple correct Answer type
Explore 109 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
Similar Questions
A resistor of resistance R is connected to a cell internal resistance 5Ω. The value of R is varied from 1Ω to 5Ω. The power consumed by R
View SolutionA battery is of emt E and internal resistance R. The value of external resistance r so that the power across eternal resistance is maximum :
View SolutionThe maximum power dissipated in an external resistance R, when connected to a cell of emf E and internal resistance r, will be
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View Solution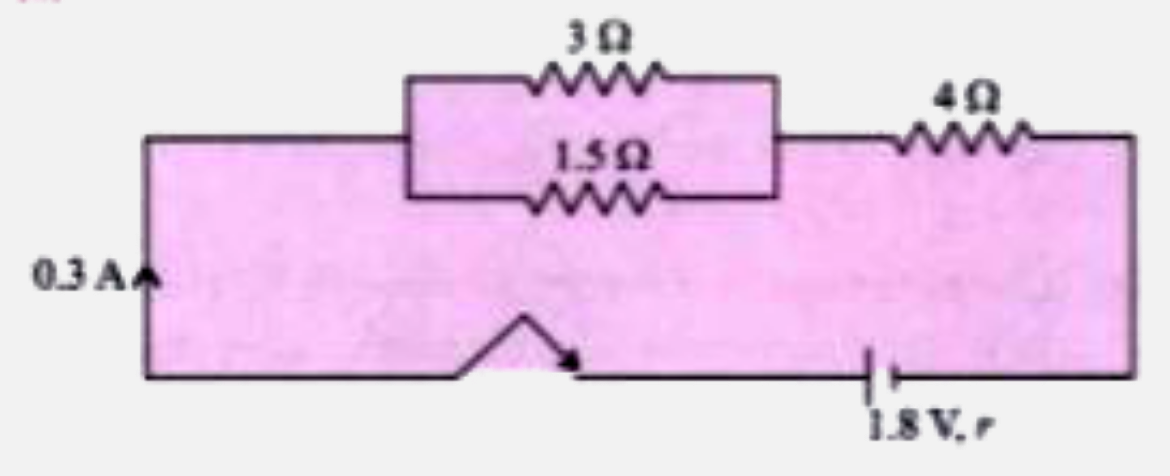
The diagram above shows three resistors connected across a cell of e.m.f. 1.8 V and internal resistance r. Calculate :
The internal resistance r.
View SolutionA cell of internal resistance r drivers current through an external resistance R. The power delivered by the to the external resistance will be maximum when:
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionA battery of ε and internal resistance r is used in a circuit with a variable external resistance R. Find the value of R for which the power consumed in R is maximum.
View SolutionIf a battery of emf E and internal resistance r is connected across a load of resistance R. Shot that the rate at which energy is dissipated in R is maximum when R=r and this maximur power is P=E2/4r.
View Solution