A battery of ε and internal resistance r is used in a circuit with a variable external resistance R. Find the value of R for which the power consumed in R is maximum.
To find the value of the external resistance R for which the power consumed in R is maximum, we can follow these steps:
Step 1: Write the expression for current I
The current I flowing through the external resistance R can be expressed using Ohm's law. The total resistance in the circuit is the sum of the internal resistance r and the external resistance R. Thus, the current I is given by:
I=ϵR+r
Step 2: Write the expression for power P
The power P consumed in the external resistance R can be expressed in terms of the current I:
P=I2R
Substituting the expression for I:
P=(ϵR+r)2R
Step 3: Simplify the power expression
Now, we simplify the expression for power P:
P=ϵ2R(R+r)2
Step 4: Differentiate power with respect to R
To find the value of R that maximizes power, we differentiate P with respect to R and set the derivative equal to zero:
dPdR=(R+r)2⋅ϵ2−2R⋅ϵ2(R+r)4=0
Step 5: Set the numerator equal to zero
We can ignore the denominator (as it cannot be zero) and set the numerator equal to zero:
(R+r)2−2R=0
Step 6: Solve for R
Expanding and rearranging gives:
R+r=2R
This simplifies to:
r=R
Conclusion
Thus, the power consumed in the external resistance R is maximum when:
R=r
The current I flowing through the external resistance R can be expressed using Ohm's law. The total resistance in the circuit is the sum of the internal resistance r and the external resistance R. Thus, the current I is given by:
The power P consumed in the external resistance R can be expressed in terms of the current I:
Now, we simplify the expression for power P:
To find the value of R that maximizes power, we differentiate P with respect to R and set the derivative equal to zero:
We can ignore the denominator (as it cannot be zero) and set the numerator equal to zero:
Expanding and rearranging gives:
Thus, the power consumed in the external resistance R is maximum when:
Topper's Solved these Questions
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Objective 1
6 Videos
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Objective 2
5 Videos
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Short Question
9 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Short answer
2 Videos
- X-RaysBOOK - HC VERMA ENGLISHCHAPTER - X-RaysEXERCISE - Ques for Short Ans
10 Videos
Similar Questions
Knowledge Check
A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A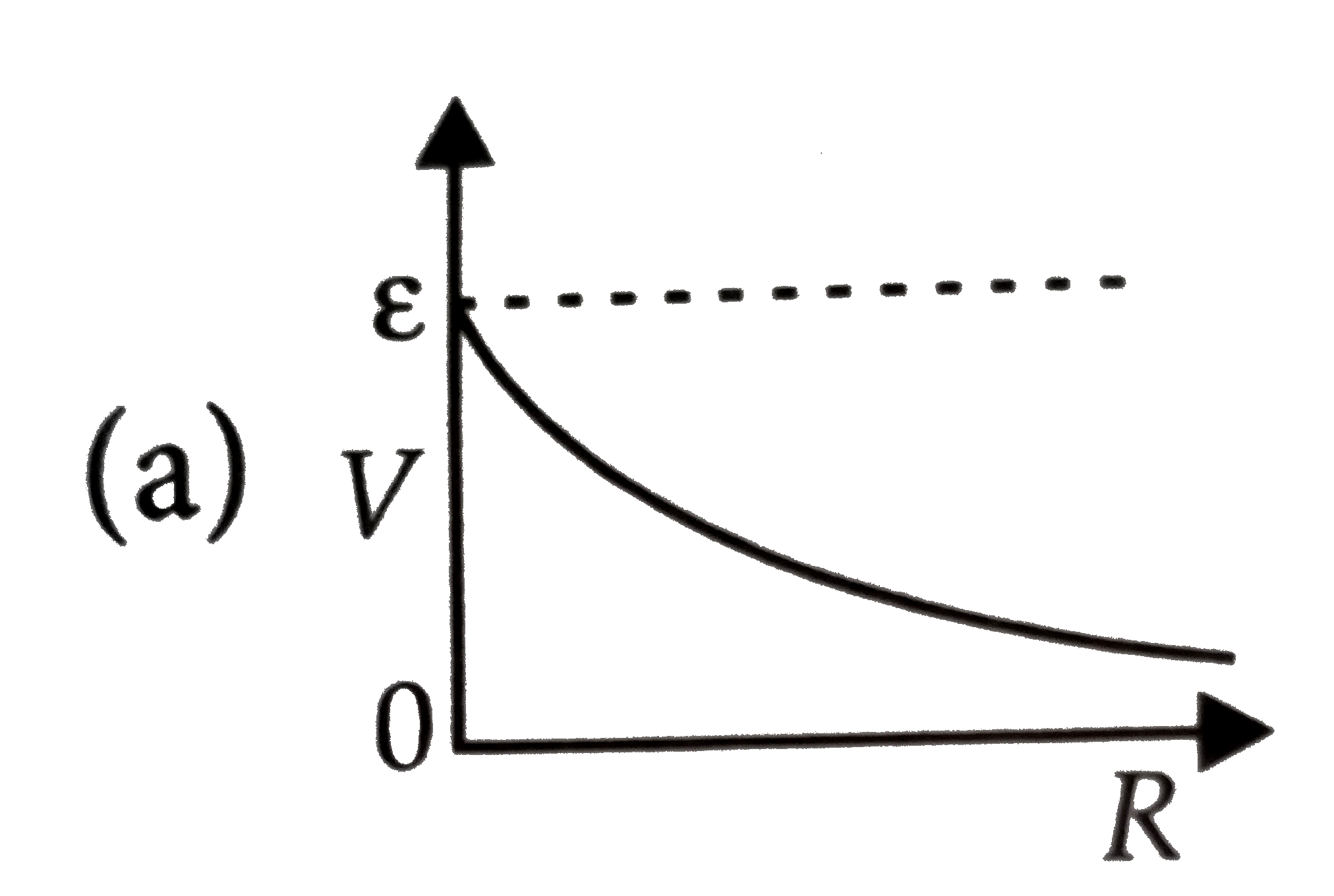 B
B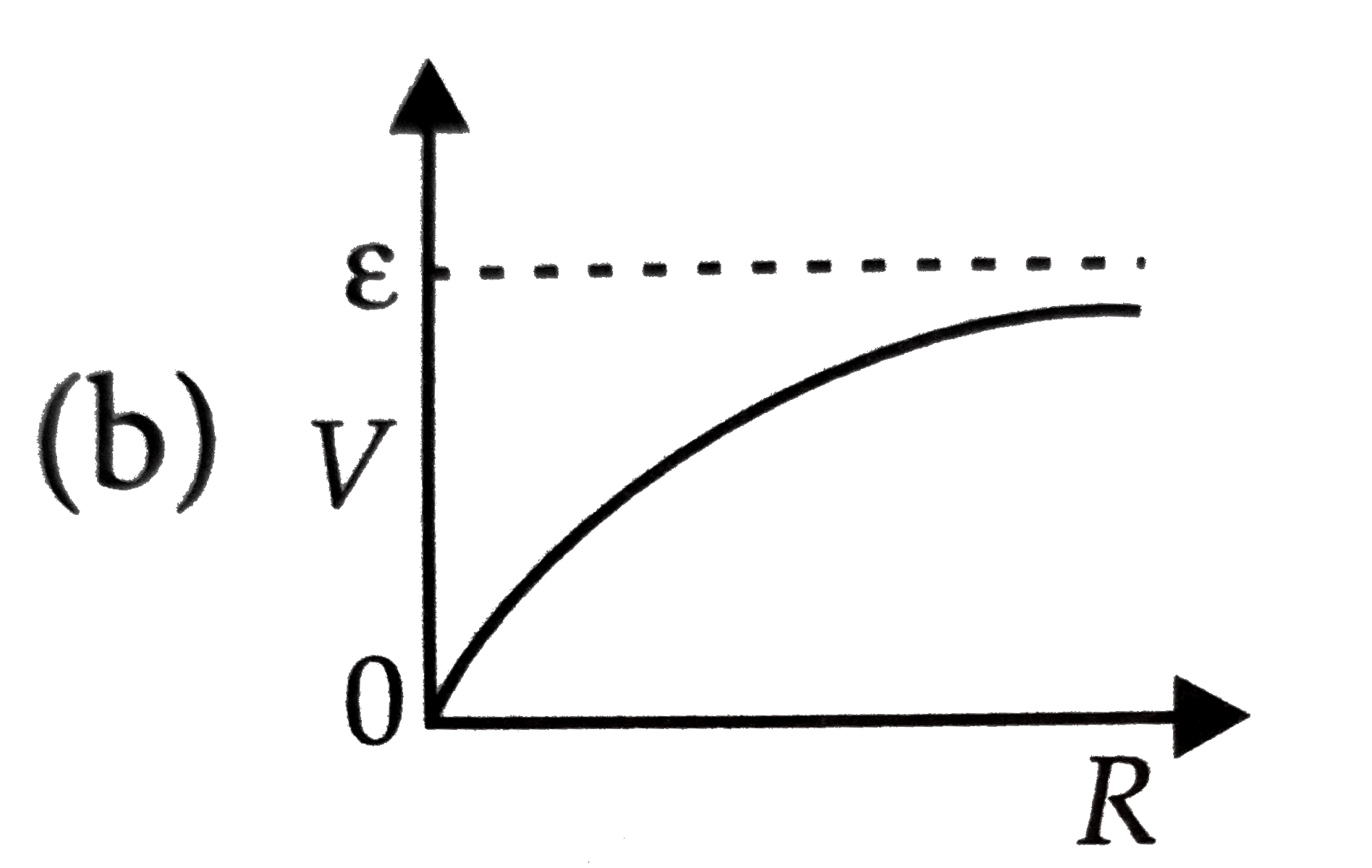 C
C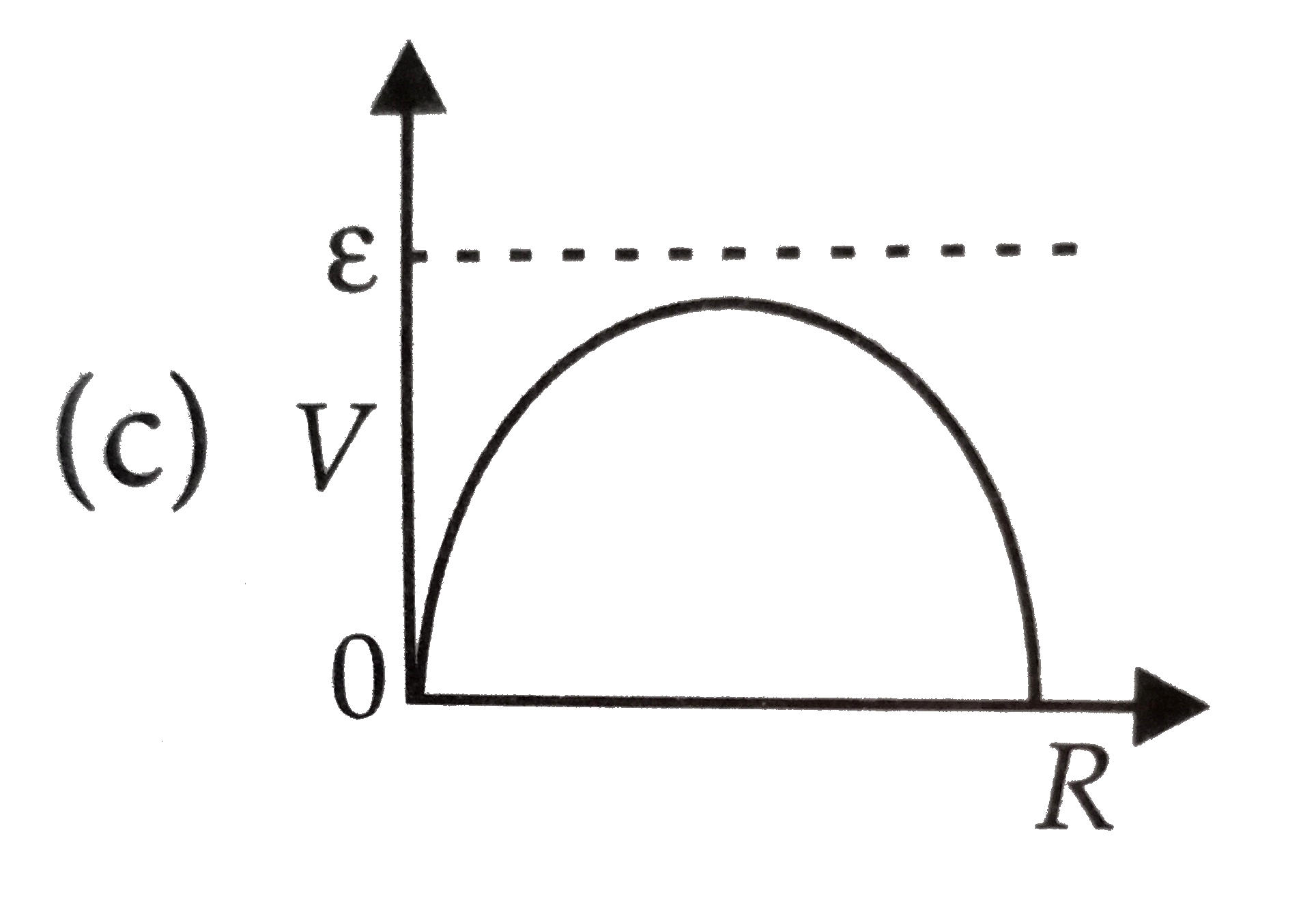 D
D
2A cell having an emf ε and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
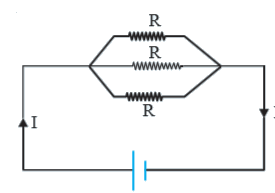
View SolutionThree equal resistances, each of RΩ are connected as shown in figure. A battery of emf 2 V and internal resistance 0.1Ω is connected across the circuit. Calculate the value of R for which the heat generated in the circuit is maximum?
View SolutionA cell of emf ε and internal resistance r drives a current i through an extermal resistance R
(i) The cell suppllied εi power
(ii) Heat is produced in R at the rate εi
(iii) Heat is produced in R at the rate εI(RR+r)
(iv) Heat is produced in the cell at the rate εi(rR+r)
View SolutionThe relation between R and r (internal resistance of the battery) for which the power consumed in the external part of the circuit is maximum.
View SolutionA battery is of emt E and internal resistance R. The value of external resistance r so that the power across eternal resistance is maximum :
View SolutionIf a battery of emf E and internal resistance r is connected across a load of resistance R. Shot that the rate at which energy is dissipated in R is maximum when R=r and this maximur power is P=E2/4r.
View Solution
