A 50 V battery is supplying current of 10 A when connected to a resistor. If the efficiency of the battery at this current is 25%, then the internal resistance of the battery is
2.5Ω
3.75Ω
1.25Ω
5Ω
The correct Answer is:B
To find the internal resistance of the battery, we can follow these steps:
Step 1: Understand the given information
We have a battery with:
- EMF (Electromotive Force) V=50V
- Current I=10A
- Efficiency η=25%
Step 2: Write the formula for efficiency
Efficiency (η) of the battery can be expressed as:
η=Power delivered to the external resistorPower supplied by the battery×100
This can be rewritten as:
η=PidealPreal
Step 3: Calculate power in ideal and real conditions
- The power delivered to the external resistor (ideal power) is given by:
Pideal=I2R
- The total power supplied by the battery (real power) is given by:
Preal=I2(R+r)
where R is the external resistance and r is the internal resistance.
Step 4: Set up the efficiency equation
Substituting the expressions for power into the efficiency equation, we have:
I2RI2(R+r)=25100
This simplifies to:
RR+r=14
Step 5: Cross-multiply and rearrange
Cross-multiplying gives:
4R=R+r
Rearranging this, we find:
r=4R−R=3R
Step 6: Use Ohm's Law to find the relationship between voltage, current, and resistance
From Ohm's Law, we know:
V=I(R+r)
Substituting the values we have:
50=10(R+r)
This simplifies to:
R+r=5(1)
Step 7: Substitute r=3R into equation (1)
Now substituting r=3R into equation (1):
R+3R=5
This simplifies to:
4R=5
Step 8: Solve for R
Dividing both sides by 4 gives:
R=54ohm
Step 9: Calculate internal resistance r
Now substituting R back into the equation for internal resistance:
r=3R=3×54=154ohm
Step 10: Final answer
Thus, the internal resistance of the battery is:
r=3.75ohm
We have a battery with:
- EMF (Electromotive Force) V=50V
- Current I=10A
- Efficiency η=25%
Efficiency (η) of the battery can be expressed as:
η=Power delivered to the external resistorPower supplied by the battery×100
This can be rewritten as:
η=PidealPreal
- The power delivered to the external resistor (ideal power) is given by:
Pideal=I2R
- The total power supplied by the battery (real power) is given by:
Preal=I2(R+r)
where R is the external resistance and r is the internal resistance.
Substituting the expressions for power into the efficiency equation, we have:
I2RI2(R+r)=25100
This simplifies to:
RR+r=14
Cross-multiplying gives:
4R=R+r
Rearranging this, we find:
r=4R−R=3R
From Ohm's Law, we know:
V=I(R+r)
Substituting the values we have:
50=10(R+r)
This simplifies to:
R+r=5(1)
Now substituting r=3R into equation (1):
R+3R=5
This simplifies to:
4R=5
Dividing both sides by 4 gives:
R=54ohm
Now substituting R back into the equation for internal resistance:
r=3R=3×54=154ohm
Thus, the internal resistance of the battery is:
r=3.75ohm
Similar Questions
A 50V battery is connected across a 10 ohm resistor. The current is 4.5A is flowing through the resistor then the internal resistance of the battery is
View SolutionA high resistance voltmeter measures the potential difference across a battery to be 9-0 V. On connecting a 24 2 resistor across the terminals of the battery, the voltmeter reads 7.2 V. Calculate the internal resistance of the battery.
View Solution
Knowledge Check
A battery having 12V emf and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 1A, then the resistance of resistor and lost voltage of the battery when circuit is closed will be
A7Ω,7VB8Ω,8VC9Ω,9VD9Ω,10V
Find the current supplied by the battery ?
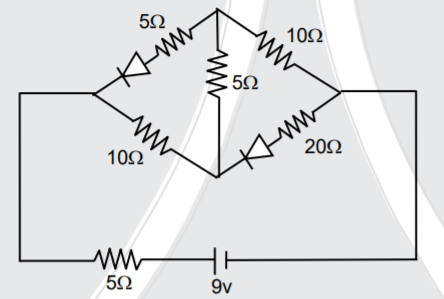
View SolutionA galvanometer, together with an unknown resistance in series, is connected across two identical batteries of each 1.5V. When the batteries are connected in series,the galvanometer records a current of 1A, and when the batteries are connected in parallel, the current is 0.6A. In this case, the internal resistance of the battery is
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View SolutionA car has a fresh storage battery of emt 12V and internal resistance 5.0×10−2Ω. If the starter moter draws a current of 90A, what is the terminal voltage of the battery when the starter is on?
(b) After long use, the internal resistance of the storange battery increase to 500Ω. What maximum current can be drawn from the battery? Assume the emt of the battery to remain unchanged.
(c) If the discharged battery is changed by an external emf source, is the terminal voltage of the battery during changing greater of less than is emf 12V?
View SolutionA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View SolutionA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View SolutionA battery of EMF E produces currents 4 A and 3 A when connected to external resistance 1Ω and 2Ω respectively. The internal resistance of the battery is
View Solution
