A battery having 12V emf and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 1A, then the resistance of resistor and lost voltage of the battery when circuit is closed will be
7Ω,7V
8Ω,8V
9Ω,9V
9Ω,10V
The correct Answer is:C
To solve the problem step by step, we will find the external resistance and the lost voltage of the battery when the circuit is closed.
Step 1: Understand the Circuit
We have a battery with an EMF (Electromotive Force) of 12V and an internal resistance of 3Ω. The battery is connected to an external resistor (let's call it R) and the current flowing through the circuit is given as 1A.
Step 2: Apply Ohm's Law
According to Ohm's law, the total voltage in the circuit is equal to the sum of the voltage drops across the internal resistance and the external resistance. The formula can be expressed as:
I=ER+r
Where:
- I = current (1A)
- E = EMF of the battery (12V)
- R = external resistance (unknown)
- r = internal resistance (3Ω)
Step 3: Substitute Known Values
Substituting the known values into the equation:
1=12R+3
Step 4: Solve for R
Cross-multiplying gives:
R+3=12
Now, isolate R:
R=12−3
R=9Ω
Step 5: Calculate the Lost Voltage
The lost voltage (or terminal voltage) of the battery can be calculated using the formula:
V=E−I⋅r
Where:
- V = terminal voltage
- E = EMF of the battery (12V)
- I = current (1A)
- r = internal resistance (3Ω)
Substituting the known values:
V=12−(1⋅3)
V=12−3
V=9V
Final Results
- The resistance of the external resistor R is 9Ω.
- The lost voltage (terminal voltage) of the battery is 9V.
We have a battery with an EMF (Electromotive Force) of 12V and an internal resistance of 3Ω. The battery is connected to an external resistor (let's call it R) and the current flowing through the circuit is given as 1A.
According to Ohm's law, the total voltage in the circuit is equal to the sum of the voltage drops across the internal resistance and the external resistance. The formula can be expressed as:
I=ER+r
Where:
- I = current (1A)
- E = EMF of the battery (12V)
- R = external resistance (unknown)
- r = internal resistance (3Ω)
Substituting the known values into the equation:
1=12R+3
Cross-multiplying gives:
R+3=12
Now, isolate R:
R=12−3
R=9Ω
The lost voltage (or terminal voltage) of the battery can be calculated using the formula:
V=E−I⋅r
Where:
- V = terminal voltage
- E = EMF of the battery (12V)
- I = current (1A)
- r = internal resistance (3Ω)
V=12−(1⋅3)
V=12−3
V=9V
- The resistance of the external resistor R is 9Ω.
- The lost voltage (terminal voltage) of the battery is 9V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - KIRCHOFF S LAW
14 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - WHEATSTONE BRIDGE
6 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - COMBINED OF RESISTORS;
23 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason
30 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistors ? What is the terminal voltage of the battery when the circuit is closed ?
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View Solution
Knowledge Check
A battery of emf 15 V and internal resistance of 4Ω is connected to a resistor. If the current in the circuit is 2A and the circuit is closed. Resistance of the resistor and terminal voltage of the battery will be
A2.5Ω,6VB3.5Ω,6VC2.5Ω,7VD3.5Ω,7V
A battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
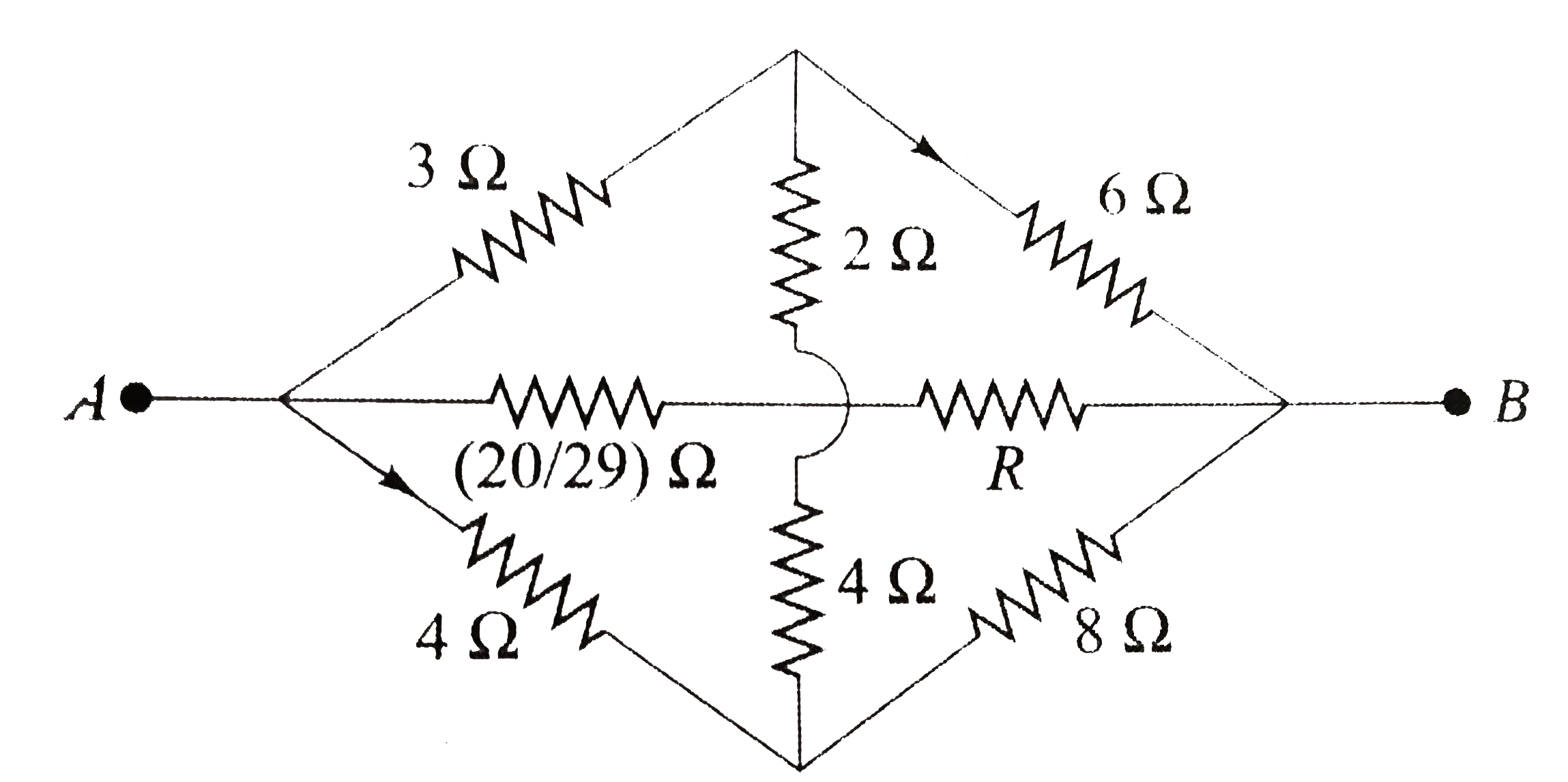 .
.
View SolutionWhen a 12V battery is connected across an unknown resistor, there is a current of 2.5mA in the circuit. Find the value of the resistance of the resistor.
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 3 Ω resistor,
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 6 Ω resistor.
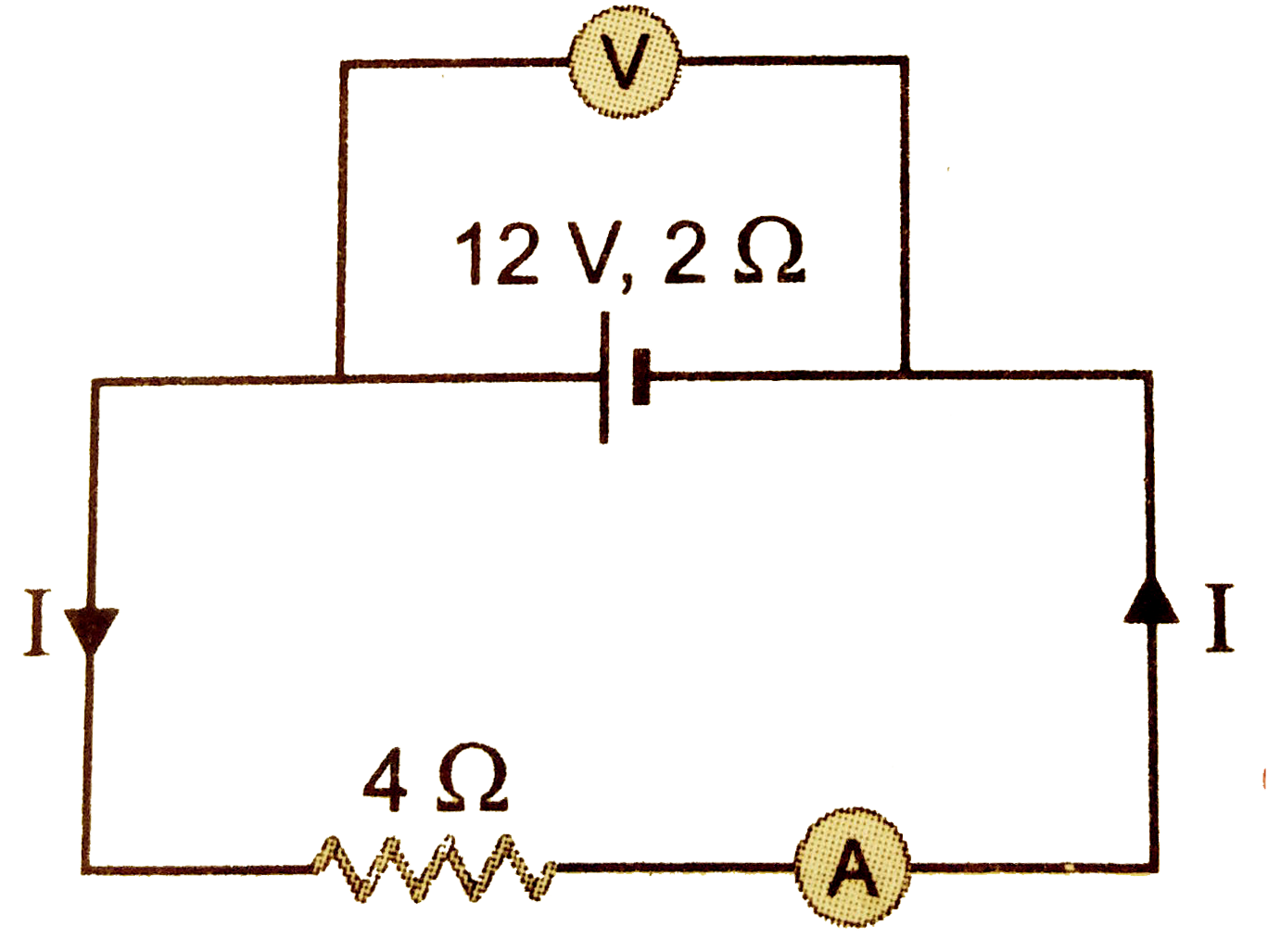
View SolutionA battery of emf 12V and internal resistance 2Ω is connected two a 4Ω resistor. Show that the a voltmeter when placed across cell and across the resistor in turn given the same reading
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the p.d. between the terminals of the battery,
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View Solution
