When a current of 2 A flows in a battery from negative to positive terminal, the potential difference across it is 12 V. If a current of 3 A flowing in the opposite direction produces a potential difference of 15 V, the emf of the battery is
12.6V
13.2V
13.5V
14.0V
The correct Answer is:B
To solve the problem, we need to determine the electromotive force (emf) of the battery based on the given current and potential differences. We will use the relationship between emf, terminal voltage, current, and internal resistance.
1. Identify the given values:
- For the first case:
- Current I1=2A
- Potential difference V1=12V
- For the second case:
- Current I2=3A (in the opposite direction)
- Potential difference V2=15V
2. Write the equations for terminal voltage:
- The terminal voltage V can be expressed as:
V=E−I⋅R
- For the first case:
V1=E−I1⋅R⟹12=E−2R(Equation 1)
- For the second case (current flowing in the opposite direction):
V2=E−I2⋅R⟹15=E−3R(Equation 2)
3. Rearrange both equations to express E:
- From Equation 1:
E=12+2R(Equation 3)
- From Equation 2:
E=15+3R(Equation 4)
4. Set the two expressions for E equal to each other:
12+2R=15+3R
5. Solve for R:
- Rearranging gives:
12−15=3R−2R⟹−3=R
- Thus, R=3Ω.
6. Substitute R back into one of the equations to find E:
- Using Equation 3:
E=12+2(3)=12+6=18V
7. Final answer:
- The emf of the battery is E=18V.
- For the first case:
- Current I1=2A
- Potential difference V1=12V
- For the second case:
- Current I2=3A (in the opposite direction)
- Potential difference V2=15V
- The terminal voltage V can be expressed as:
V=E−I⋅R
- For the first case:
V1=E−I1⋅R⟹12=E−2R(Equation 1)
- For the second case (current flowing in the opposite direction):
V2=E−I2⋅R⟹15=E−3R(Equation 2)
- From Equation 1:
E=12+2R(Equation 3)
- From Equation 2:
E=15+3R(Equation 4)
12+2R=15+3R
- Rearranging gives:
12−15=3R−2R⟹−3=R
- Thus, R=3Ω.
- Using Equation 3:
E=12+2(3)=12+6=18V
- The emf of the battery is E=18V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - KIRCHOFF S LAW
14 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - WHEATSTONE BRIDGE
6 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - COMBINED OF RESISTORS;
23 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason
30 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Potential difference across the terminal of a non ideal battery is
View SolutionA current 0.2A flows in a wire of resistance 15Ω. Find the potential difference across the ends of the wire.
View SolutionThe potential difference across the terminals of a battery is 10 V when there is a current of 3 A in the battery from the negative to the positive terminal. When the current is 2A in the reverse direction, the potential difference becomes 15 V. The internal resistance of the battery is
View SolutionA current of 2A flows in a system of conductor as shown. The potential difference (VA−VB)
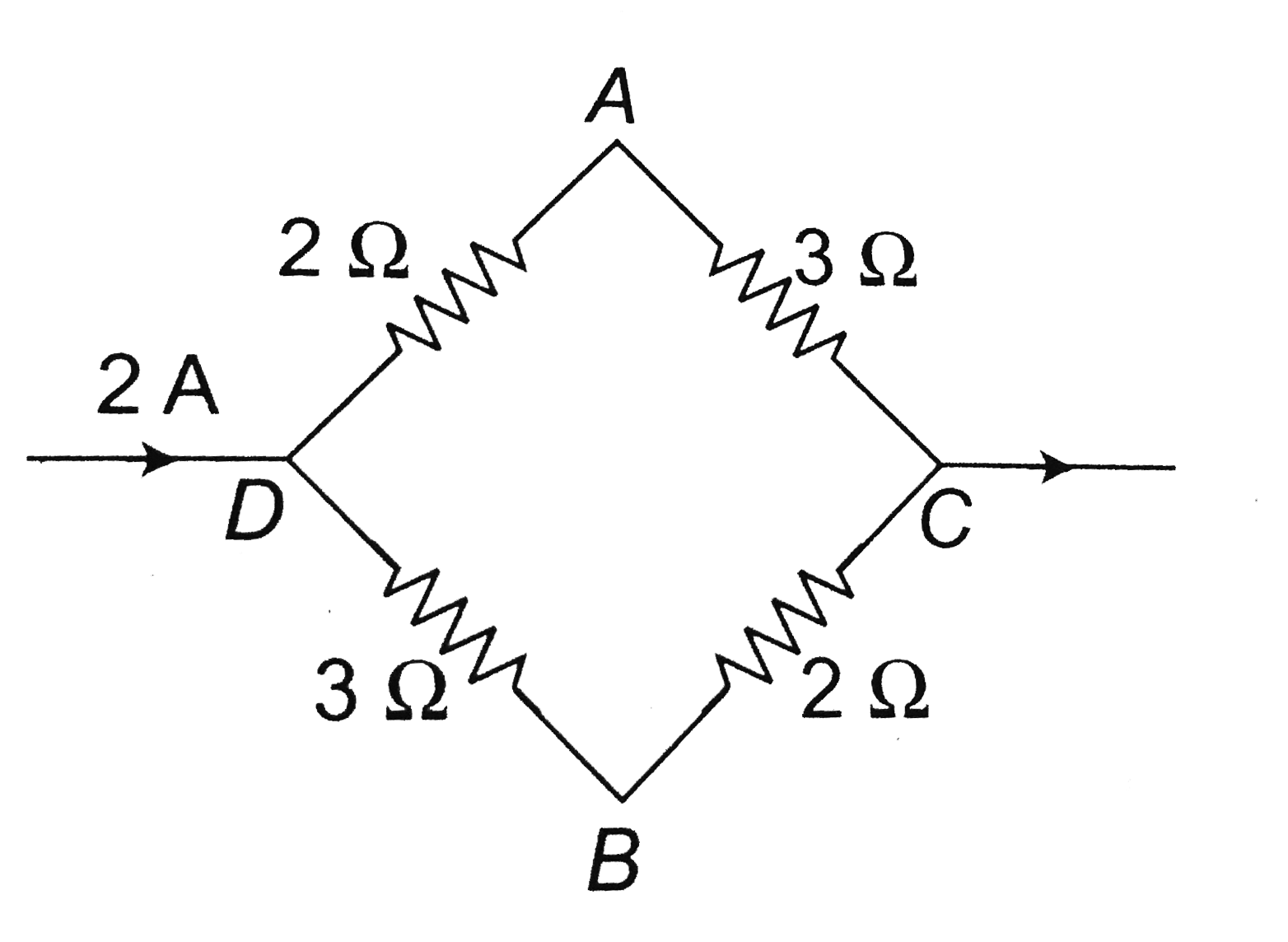
View SolutionA current of 2A flows in a system of conductor as shown. The potential difference (VA−VB)

View SolutionA current of 2A flows in a system of conductor as shown. The potential difference (VA−VB)

View SolutionThe displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
View SolutionThe displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
View SolutionThe potential difference across the terminals of a battery is 8.4V when there is a current of 1.50A in the battery from the negative to the positive terminal. When the current is 3.50Air, the reverse direction, the potential difference becomes 9.4V.
(a) What is the internal resistance of the battery?
(b) What is the emf of the battery?
View SolutionCan the potential difference across a battery be greater than its emf?
View Solution
