The corners A, B, C, and D of a square are occupied by charges q,−q,2Q, and Q, respectively. The side of square is 2b. The field at the midpoint of side CD is zero. What is the value of q/Q?
5sart5/2
2√2/5
2/5
5/2
The correct Answer is:A
To solve the problem, we need to find the ratio qQ given that the electric field at the midpoint of side CD of a square with charges q,−q,2Q, and Q at corners A, B, C, and D respectively is zero. The side of the square is 2b.
1. Understanding the Setup:
- We have a square with corners A, B, C, and D.
- Charges at the corners are:
- A: q
- B: −q
- C: 2Q
- D: Q
- The side length of the square is 2b.
2. Identify the Midpoint M:
- The midpoint M of side CD is located at coordinates (b,0) if we place:
- A at (0,2b)
- B at (0,0)
- C at (2b,2b)
- D at (2b,0)
3. Calculate Distances:
- The distances from M to each charge are:
- Distance from M to A: AM=√(b−0)2+(0−2b)2=√b2+4b2=√5b2=b√5
- Distance from M to B: BM=√(b−0)2+(0−0)2=b
- Distance from M to C: CM=√(b−2b)2+(0−2b)2=√(−b)2+(−2b)2=√5b2=b√5
- Distance from M to D: DM=√(b−2b)2+(0−0)2=b
4. Calculate Electric Fields:
- The electric field E due to a point charge is given by E=k|Q|r2 where k is Coulomb's constant.
- Electric field contributions at M:
- Due to charge A:
EA=kq(b√5)2=kq5b2
(Directed away from A)
- Due to charge B:
EB=k−qb2=−kqb2
(Directed towards B)
- Due to charge C:
EC=k2Q(b√5)2=2kQ5b2
(Directed away from C)
- Due to charge D:
ED=kQb2=kQb2
(Directed away from D)
5. Setting Up the Electric Field Equation:
- The net electric field at M must be zero:
EA+EB+EC+ED=0
- Substituting the values:
kq5b2−kqb2+2kQ5b2+kQb2=0
6. Simplifying the Equation:
- Combine like terms:
(kq5b2−5kq5b2)+(2kQ5b2+5kQ5b2)=0
- This simplifies to:
−4kq5b2+7kQ5b2=0
- Rearranging gives:
4q=7Q
7. Finding the Ratio:
- Thus, the ratio qQ is:
qQ=74
Final Answer:
qQ=74
- We have a square with corners A, B, C, and D.
- Charges at the corners are:
- A: q
- B: −q
- C: 2Q
- D: Q
- The side length of the square is 2b.
- The midpoint M of side CD is located at coordinates (b,0) if we place:
- A at (0,2b)
- B at (0,0)
- C at (2b,2b)
- D at (2b,0)
- The distances from M to each charge are:
- Distance from M to A: AM=√(b−0)2+(0−2b)2=√b2+4b2=√5b2=b√5
- Distance from M to B: BM=√(b−0)2+(0−0)2=b
- Distance from M to C: CM=√(b−2b)2+(0−2b)2=√(−b)2+(−2b)2=√5b2=b√5
- Distance from M to D: DM=√(b−2b)2+(0−0)2=b
- The electric field E due to a point charge is given by E=k|Q|r2 where k is Coulomb's constant.
- Electric field contributions at M:
- Due to charge A:
EA=kq(b√5)2=kq5b2
(Directed away from A)
- Due to charge B:
EB=k−qb2=−kqb2
(Directed towards B)
- Due to charge C:
EC=k2Q(b√5)2=2kQ5b2
(Directed away from C)
- Due to charge D:
ED=kQb2=kQb2
(Directed away from D)
- The net electric field at M must be zero:
EA+EB+EC+ED=0
- Substituting the values:
kq5b2−kqb2+2kQ5b2+kQb2=0
- Combine like terms:
(kq5b2−5kq5b2)+(2kQ5b2+5kQ5b2)=0
- This simplifies to:
−4kq5b2+7kQ5b2=0
- Rearranging gives:
4q=7Q
- Thus, the ratio qQ is:
qQ=74
qQ=74
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
Four point charge q,−q,2Q and Q are placed in order at the corners A, B, C and D of a square. If the field at the midpoint of CD is zero then the value of q/Q is 5√5x. Find the value of x.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The electric potential at O is.View Solution
Knowledge Check
- Question 1 - Select One
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2Dzero
Four charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. If O is the center of square.
The electric field at O is.View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The work done in carrying a charge e from O to F is.View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The work done in carrying a charge e from O to E is.View SolutionThree concentric spherical shells A, B and C having uniformly distributed total charges +Q, -2Q and +Q respectively are placed as shown. The potential at the centre will be -
 View Solution
View SolutionFour charges equal to −Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is
View Solution(Figure 3.78) shows three thin concentric spherical shells A, B and C with initial charges on A , B, and C as 3 Q, 2Q, and -Q, respectively. The shells A amd C are connected by a wire such that it does not touch B. Shell B is earthed. Determine the final charges qA,qB,andqC.
 .View Solution
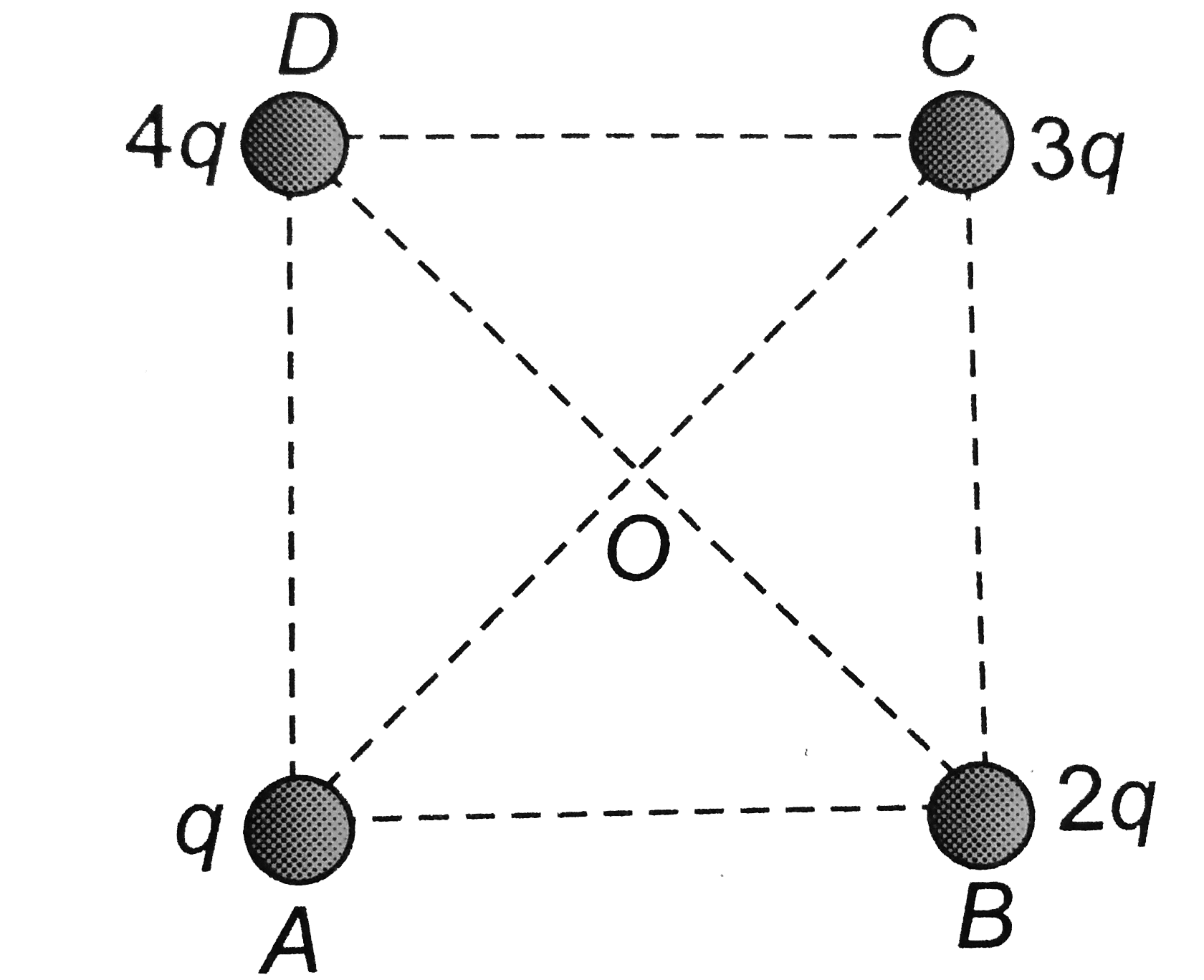
.View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along
 View Solution
View Solution
