In the above question, if plates P1andP2 are connected by a thin conducting wire, then the amount of heat produced will be
Q2Aε0d
5Q2Aε0d
2Q2Aε0d
none of these
The correct Answer is:D
To solve the problem regarding the amount of heat produced when plates P1 and P2 are connected by a thin conducting wire, we will follow these steps:
Step 1: Understand the System
When two charged plates are connected by a conducting wire, they will reach the same electric potential. The charge will redistribute between the plates until equilibrium is reached.
Step 2: Determine the Initial Charge on the Plates
Let’s denote the initial charges on plates P1 and P2 as Q1 and Q2 respectively. The potential difference between the plates can be expressed as:
V=Q1C1−Q2C2
where C1 and C2 are the capacitances of plates P1 and P2.
Step 3: Calculate the Final Charge Distribution
After connecting the plates with a wire, the total charge Qt=Q1+Q2 will redistribute between the two plates. The final charges on the plates can be expressed as:
Q′1=C1VfandQ′2=C2Vf
where Vf is the final common potential.
Step 4: Calculate the Heat Produced
The heat produced Qh due to the redistribution of charge can be calculated using the energy stored in the capacitors before and after the connection:
Qh=(12Q21C1+12Q22C2)−(12(Q1+Q2)2Ceq)
where Ceq is the equivalent capacitance of the two capacitors in parallel:
Ceq=C1+C2
Step 5: Substitute and Simplify
Substituting the expressions for Qh and simplifying will yield the final expression for the heat produced.
Final Expression
Qh=12(Q21C1+Q22C2−(Q1+Q2)2Ceq)
When two charged plates are connected by a conducting wire, they will reach the same electric potential. The charge will redistribute between the plates until equilibrium is reached.
Let’s denote the initial charges on plates P1 and P2 as Q1 and Q2 respectively. The potential difference between the plates can be expressed as:
V=Q1C1−Q2C2
where C1 and C2 are the capacitances of plates P1 and P2.
After connecting the plates with a wire, the total charge Qt=Q1+Q2 will redistribute between the two plates. The final charges on the plates can be expressed as:
Q′1=C1VfandQ′2=C2Vf
where Vf is the final common potential.
The heat produced Qh due to the redistribution of charge can be calculated using the energy stored in the capacitors before and after the connection:
Qh=(12Q21C1+12Q22C2)−(12(Q1+Q2)2Ceq)
where Ceq is the equivalent capacitance of the two capacitors in parallel:
Ceq=C1+C2
Substituting the expressions for Qh and simplifying will yield the final expression for the heat produced.
Qh=12(Q21C1+Q22C2−(Q1+Q2)2Ceq)
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
P1 and P2 are respectively :
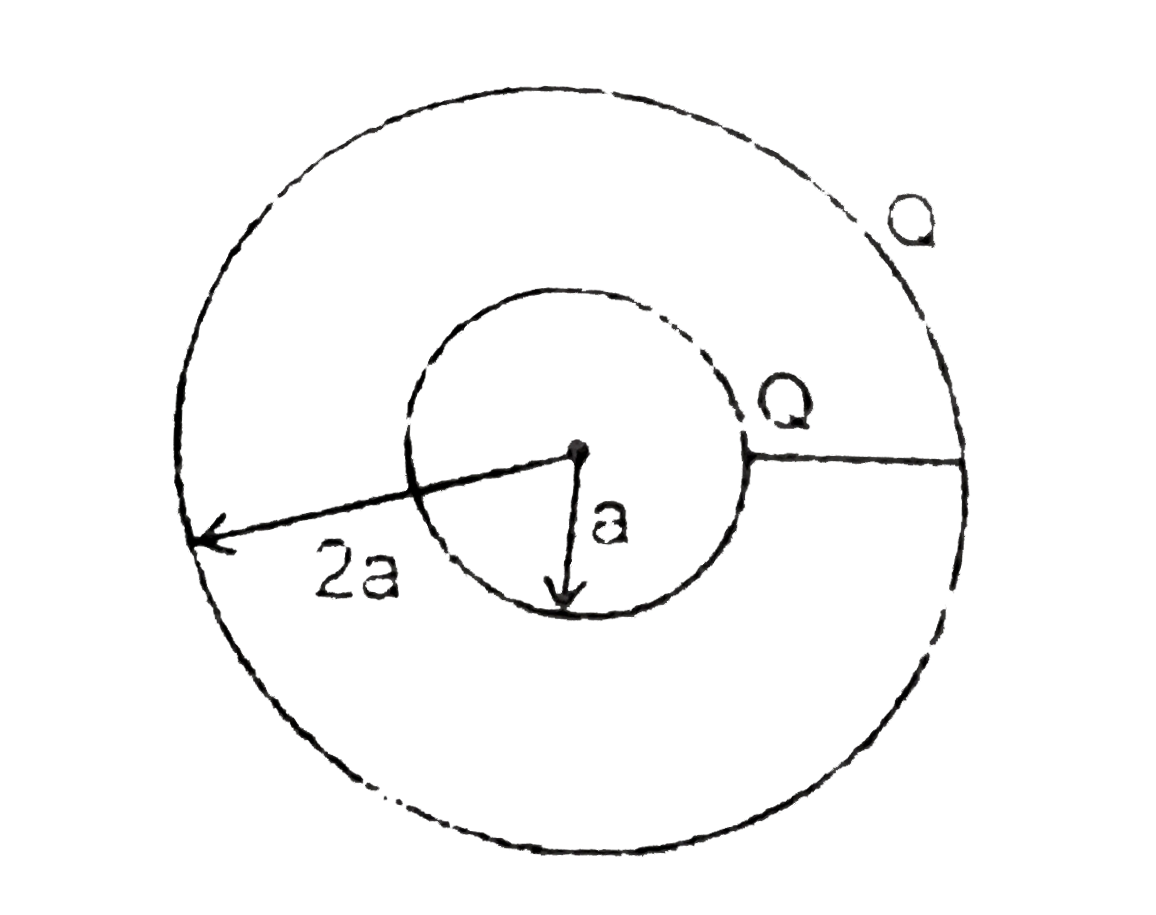
View SolutionFigure shows a solid metal sphere of radius a surrounded by a concentric thin metal shell of radius 2a. Initially both are having charges Q each, When the two are connected by a conducting wire as shown in the figure, then amount of heat produced in this process will be :
View SolutionThe capacities of two conductors are C1 and C2 and their respectively potentials are V1 and V2. If they are connected by a thin wire, then the loss of energy will be given by
View SolutionFour identical metal plates are arranged as shown plates 1 and 4 are connected by a connecting wire. A battery of emf V volts is connected between plates 2 and 3. The electric field between plates 3 and 4 is 2VKd. Find the value of K

View SolutionA 2μF capacitor is charged to 100V, and then its plates are connected by a conducting Wire. The heat produced is .
View SolutionThree identical metallic plates are kept parallel to one another at separations a & b as shown in figure. The outer plates are connected by a thin conducting wire and a charge Q is placed on the central plate. Find the charge on all the six sufaces.
View SolutionWhen two concentric shells are connected by a thin conducting wire, whole of the charge of inner shell transfers to the outer shell and potential difference between them becomes zero. Surface charge densities of two thin concentric spherical shells are σ and −σ respectively. Their radii are R and 2R. Now they are connected by a thin wire.

Suppose electric field at a distance r(>2R) was E1 before connecting the two shells and E2 after connecting the two shells, then ∣∣∣E2E1∣∣∣ is :-
View SolutionFive conducting parallel plates having area A and separation between them d, are placed as shown in the fig. Plate number 2 and 4 are connected with a conducting wire and between point A and B a cell of emf. .ε. is connected . The change flows through the cell is
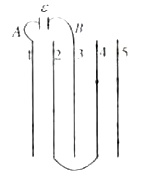
View SolutionA long resistance wire is divided into 2n parts. Then n parts are connected in series and the other n parts in parallel separately. Both combinations are connected to identical supplies. Then the ratio of heat produced in series to parallel combinations will be -
View SolutionTwo concentric hollow conducting spheres of radius a and b (b>a) contains charges Qa and Qb respectively. If they are connected by a conducting wire then find out following
(i) Final charges on inner and outer spheres.
(ii) Heat produced during the process.
View Solution
