Three identical metallic plates are kept parallel to one another at separations a & b as shown in figure. The outer plates are connected by a thin conducting wire and a charge Q is placed on the central plate. Find the charge on all the six sufaces.
To solve the problem of finding the charge on all six surfaces of the three identical metallic plates, we can follow these steps:
Step 1: Understand the Configuration
We have three metallic plates:
- Plate M1 (outer plate)
- Plate M2 (middle plate)
- Plate P1 (outer plate)
- Plate P2 (middle plate)
The plates are arranged parallel to each other with separations a and b. The outer plates (M1 and P2) are connected by a thin conducting wire, and a charge Q is placed on the central plate (M2).
Step 2: Define Capacitances
Define the capacitances between the plates:
- C1 is the capacitance between M2 and M1, given by:
C1=ϵ0Aa
- C2 is the capacitance between M2 and P1, given by:
C2=ϵ0Ab
Step 3: Determine Equivalent Capacitance
Since the outer plates (M1 and P2) are connected by a wire, the potential difference across both capacitors C1 and C2 is the same. Therefore, they are in parallel, and the equivalent capacitance Ceq is:
Ceq=C1+C2=ϵ0Aa+ϵ0Ab
Step 4: Calculate the Charge Distribution
The total charge Q on the central plate (M2) will distribute between the two capacitors:
- The charge on capacitor C1 (between M2 and M1) is:
Q1=C1⋅V=C1⋅QCeq=C1⋅QC1+C2
Substituting C1:
Q1=ϵ0Aa⋅Qϵ0Aa+ϵ0Ab=Q⋅ba+b
- The charge on capacitor C2 (between M2 and P1) is:
Q2=C2⋅V=C2⋅QCeq=C2⋅QC1+C2
Substituting C2:
Q2=ϵ0Ab⋅Qϵ0Aa+ϵ0Ab=Q⋅aa+b
Step 5: Determine Charges on Each Surface
Now we can find the charges on each surface:
- Charge on surface n1 (M2 facing M1):
n1=Q1=Q⋅ba+b
- Charge on surface m2 (M2 facing P1):
n2=Q2=Q⋅aa+b
- Since the plates are conductive, the charges on the adjacent surfaces must be equal and opposite:
- Charge on surface m1:
m1=−n1=−Q⋅ba+b
- Charge on surface p1:
p1=−n2=−Q⋅aa+b
- The outer plates (M1 and P2) must have zero net charge:
- Charge on surface p2:
p2=Q⋅aa+b
- Charge on surface m2:
m2=Q⋅ba+b
Final Charges on All Surfaces
- n1=Q⋅ba+b
- m1=−Q⋅ba+b
- n2=Q⋅aa+b
- p1=−Q⋅aa+b
- p2=Q⋅aa+b
- m2=Q⋅ba+b
We have three metallic plates:
- Plate M1 (outer plate)
- Plate M2 (middle plate)
- Plate P1 (outer plate)
- Plate P2 (middle plate)
Define the capacitances between the plates:
- C1 is the capacitance between M2 and M1, given by:
C1=ϵ0Aa
- C2 is the capacitance between M2 and P1, given by:
C2=ϵ0Ab
Since the outer plates (M1 and P2) are connected by a wire, the potential difference across both capacitors C1 and C2 is the same. Therefore, they are in parallel, and the equivalent capacitance Ceq is:
Ceq=C1+C2=ϵ0Aa+ϵ0Ab
The total charge Q on the central plate (M2) will distribute between the two capacitors:
- The charge on capacitor C1 (between M2 and M1) is:
Q1=C1⋅V=C1⋅QCeq=C1⋅QC1+C2
Substituting C1:
Q1=ϵ0Aa⋅Qϵ0Aa+ϵ0Ab=Q⋅ba+b
Q2=C2⋅V=C2⋅QCeq=C2⋅QC1+C2
Substituting C2:
Q2=ϵ0Ab⋅Qϵ0Aa+ϵ0Ab=Q⋅aa+b
Now we can find the charges on each surface:
- Charge on surface n1 (M2 facing M1):
n1=Q1=Q⋅ba+b
- Charge on surface m2 (M2 facing P1):
n2=Q2=Q⋅aa+b
- Since the plates are conductive, the charges on the adjacent surfaces must be equal and opposite:
- Charge on surface m1:
m1=−n1=−Q⋅ba+b
- Charge on surface p1:
p1=−n2=−Q⋅aa+b
- The outer plates (M1 and P2) must have zero net charge:
- Charge on surface p2:
p2=Q⋅aa+b
- Charge on surface m2:
m2=Q⋅ba+b
- n1=Q⋅ba+b
- m1=−Q⋅ba+b
- n2=Q⋅aa+b
- p1=−Q⋅aa+b
- p2=Q⋅aa+b
- m2=Q⋅ba+b
Similar Questions
Three identical metallic plates are kept parallel to one another at separations a and b. The outer plates are connected to the ground and the middle plate is given charge Q. Then, the charge on the right side of middle plate is

View SolutionTwo metallic plates are kept parallel to one another and charges are given to them as shown in figure. Find the charge on all the four faces.

View SolutionThree identical large metallic plates are placed parallel to each other at a very small separation as shown in. The central plate is give a charge Q. What amount of charge will flow to earth when the key is pressid?
 .
.
View SolutionThree identical metal plates with large surface areas are kept parallel to each as shown in figure (30-E8). The leftmost plate is given a charge Q, the rightmost a chrgear2Q and the middle one remains neutral. Find the charge appearing on the outer surface of the rightmost plate.
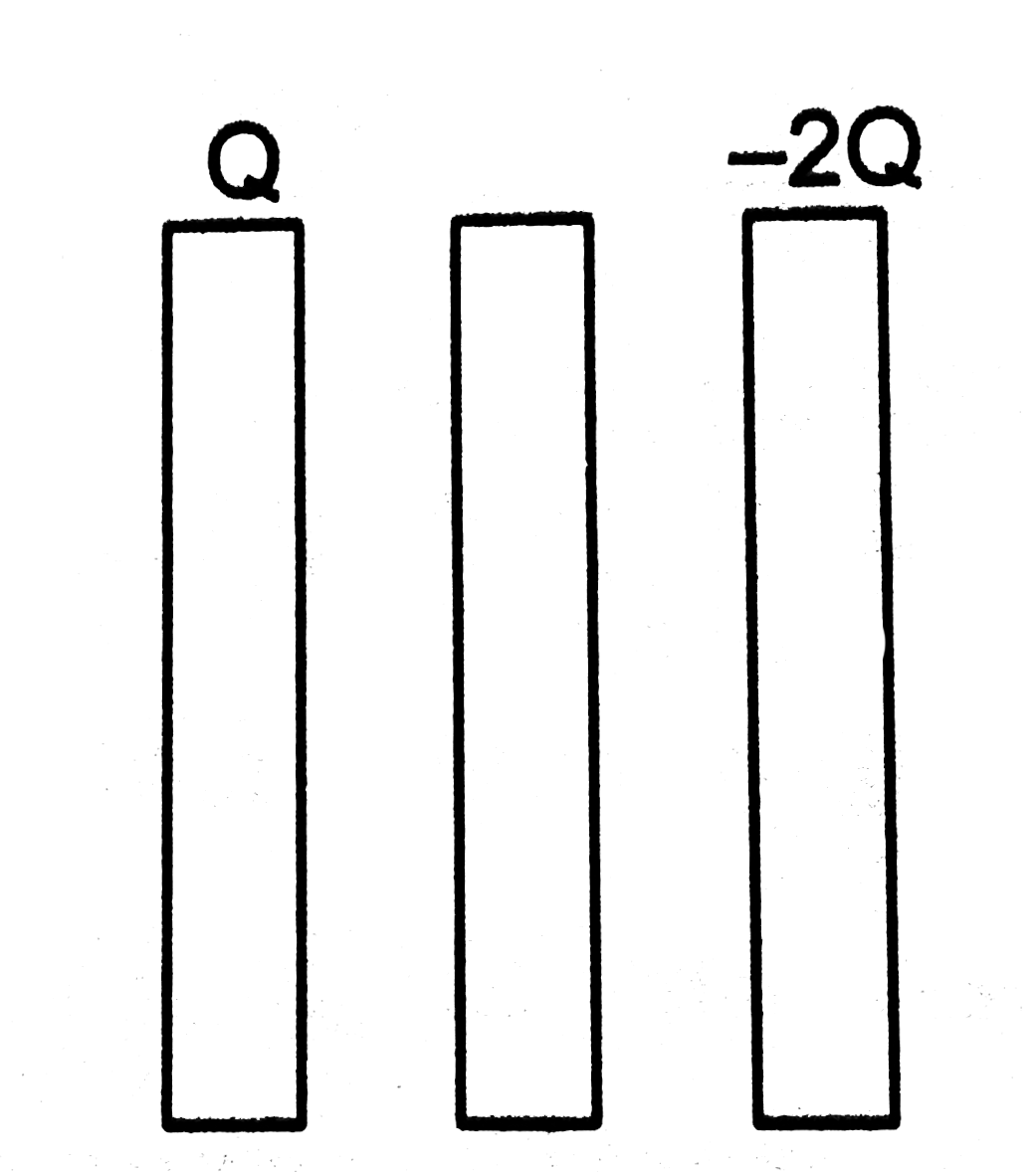
View SolutionFour very large metal plates are given charges as shown in figure. The middle two are then connected through a wire. Find the charge that will flow through the wire.

View SolutionThree identical large plates are fixed at separation of d from each other as shown in figure. The area of each plate is A. Plate 1 is given charge +Q while plates 2 and 3 are neutral and are connected to each other through coil of inductances L and switch S. If resistance of all connected wires is neglected the maximum current flow through coil after closing switch is (C=εe0Ad) (neglect fringe effect)
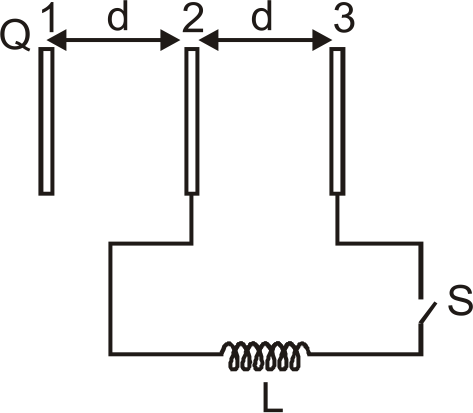
View SolutionThree charged conducting plates are separated by small distances as shown in figure. The charges on the plates are shown. Find the ratio of charge on right surface and left surface of the middle plate.

View SolutionThree metallic plates out of which the middle is given charge Q as shown in the figure. The outer plates can be earthed with the help of switches S1andS2 . The area of each plates is the same. Answer the following question based on the given passage.
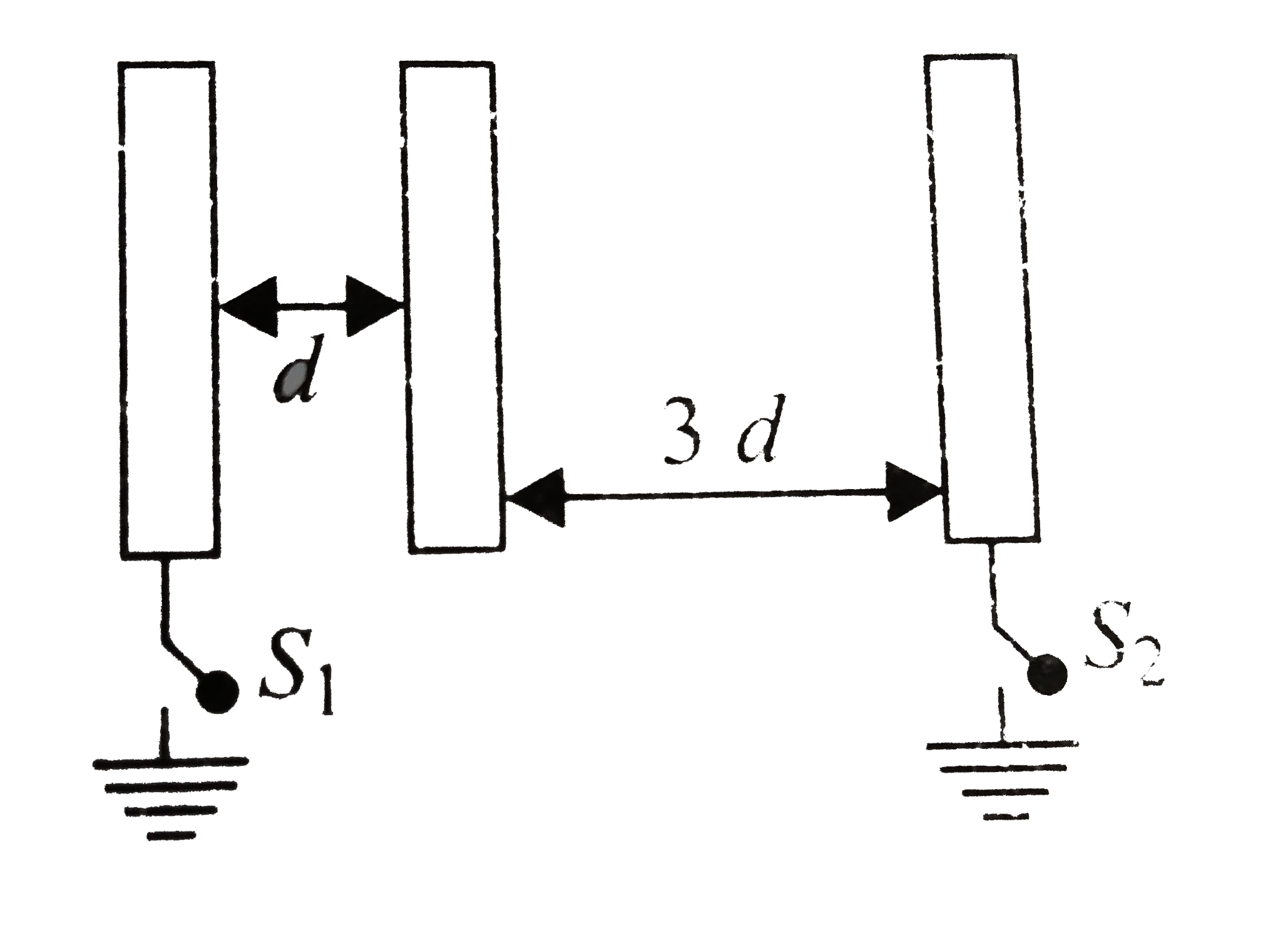
View SolutionFour large metallic plates of area A each are kept parallel to each other with a small separation between them as shown in the figure. A cell of emf V is connected across the two outermost plates through a switch K1. The two inner plates are similarly connected with a cell of emf 2 V through a switch k2 Initially both switched are open and the plates, starting form left to right (i.e. number 1 to 4) are given charges Q,2Q,−2Q and −Q respectively. Now answer the following questions

The charge appearing on the outer surface of plate -1, when switches K1,K2 are open
View SolutionFour large metallic plates of area A each are kept parallel to each other with a small separation between them as shown in the figure. A cell of emf V is connected across the two outermost plates through a switch K1. The two inner plates are similarly connected with a cell of emf 2 V through a switch k2 Initially both switched are open and the plates, starting form left to right (i.e. number 1 to 4) are given charges Q,2Q,−2Q and −Q respectively. Now answer the following questions

If K1 is closed and K2 is open the charge appearing on the right surface of plate-2 is
View Solution
