In question 15, if the conducting spherical shell is not earthed but is neutral, then the force on q2 is
zero
q1q24πε0r2
q1q24πε0(r−R)2
none of these
The correct Answer is:B
To solve the problem, we need to analyze the situation involving a neutral conducting spherical shell and a point charge q2 placed outside the shell. Here is a step-by-step solution:
Step 1: Understand the Configuration
We have a neutral conducting spherical shell and a point charge q2 located outside the shell. Since the shell is neutral and not earthed, it will not have any net charge.
Hint: Remember that a neutral conducting shell will have induced charges when an external charge is present.
Step 2: Induced Charges on the Shell
When the point charge q2 is placed outside the neutral conducting shell, it will induce charges on the inner surface of the shell. The inner surface will have a charge of −q2 (negative charge) due to the presence of q2. Consequently, the outer surface of the shell will have a charge of +q2 to maintain the neutrality of the shell.
Hint: The total charge on a conductor must remain constant; thus, induced charges will adjust accordingly.
Step 3: Analyze the Forces Acting on q2
The force on q2 is due to the electric field created by the induced charge on the outer surface of the shell. Since the shell is neutral and the charge distribution is symmetric, the electric field inside the conductor (including the cavity) is zero.
Hint: Use Gauss's law to understand that the electric field inside a conductor in electrostatic equilibrium is zero.
Step 4: Calculate the Force on q2
The force F on q2 due to the charge on the outer surface can be calculated using Coulomb's law. The effective charge acting on q2 is the total charge on the outer surface of the shell, which is +q2.
The formula for the force is given by:
F=k|q2|⋅|q1|r2
where k is Coulomb's constant, q1 is the charge on the outer surface, and r is the distance from the center of the shell to the charge q2.
Hint: Remember that the distance r is the distance from the center of the shell to the point charge q2.
Step 5: Conclusion
Since the charge on the outer surface of the shell is +q2, the force on q2 due to the shell will be repulsive. Therefore, the force on q2 is directed away from the shell.
Final Answer: The force on q2 is given by:
F=kq22r2
where the direction of the force is away from the shell.
We have a neutral conducting spherical shell and a point charge q2 located outside the shell. Since the shell is neutral and not earthed, it will not have any net charge.
When the point charge q2 is placed outside the neutral conducting shell, it will induce charges on the inner surface of the shell. The inner surface will have a charge of −q2 (negative charge) due to the presence of q2. Consequently, the outer surface of the shell will have a charge of +q2 to maintain the neutrality of the shell.
The force on q2 is due to the electric field created by the induced charge on the outer surface of the shell. Since the shell is neutral and the charge distribution is symmetric, the electric field inside the conductor (including the cavity) is zero.
The force F on q2 due to the charge on the outer surface can be calculated using Coulomb's law. The effective charge acting on q2 is the total charge on the outer surface of the shell, which is +q2.
F=k|q2|⋅|q1|r2
where k is Coulomb's constant, q1 is the charge on the outer surface, and r is the distance from the center of the shell to the charge q2.
Since the charge on the outer surface of the shell is +q2, the force on q2 due to the shell will be repulsive. Therefore, the force on q2 is directed away from the shell.
F=kq22r2
where the direction of the force is away from the shell.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
A solid metallic sphere has a charge +3Q. Concentric with this sphere is a conducting spherical shell having charge −Q. The radius of the sphere is a and that of the spherical shell is b(b>a) What is the electric field at a distance R(a<R<b) from the centre
View SolutionA solid conducting sphere, having a charge Q, is surrounded by an unchanged conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a change of −4Q, the new potential difference between the same tow surface is :
View SolutionA metal sphere of radius 'a' is having charge +Q. Now it is connected by a conducting wire concentric spherical shell of radius '2a'. Then the potential at the surface of outer shell is

Here, K=14πε0
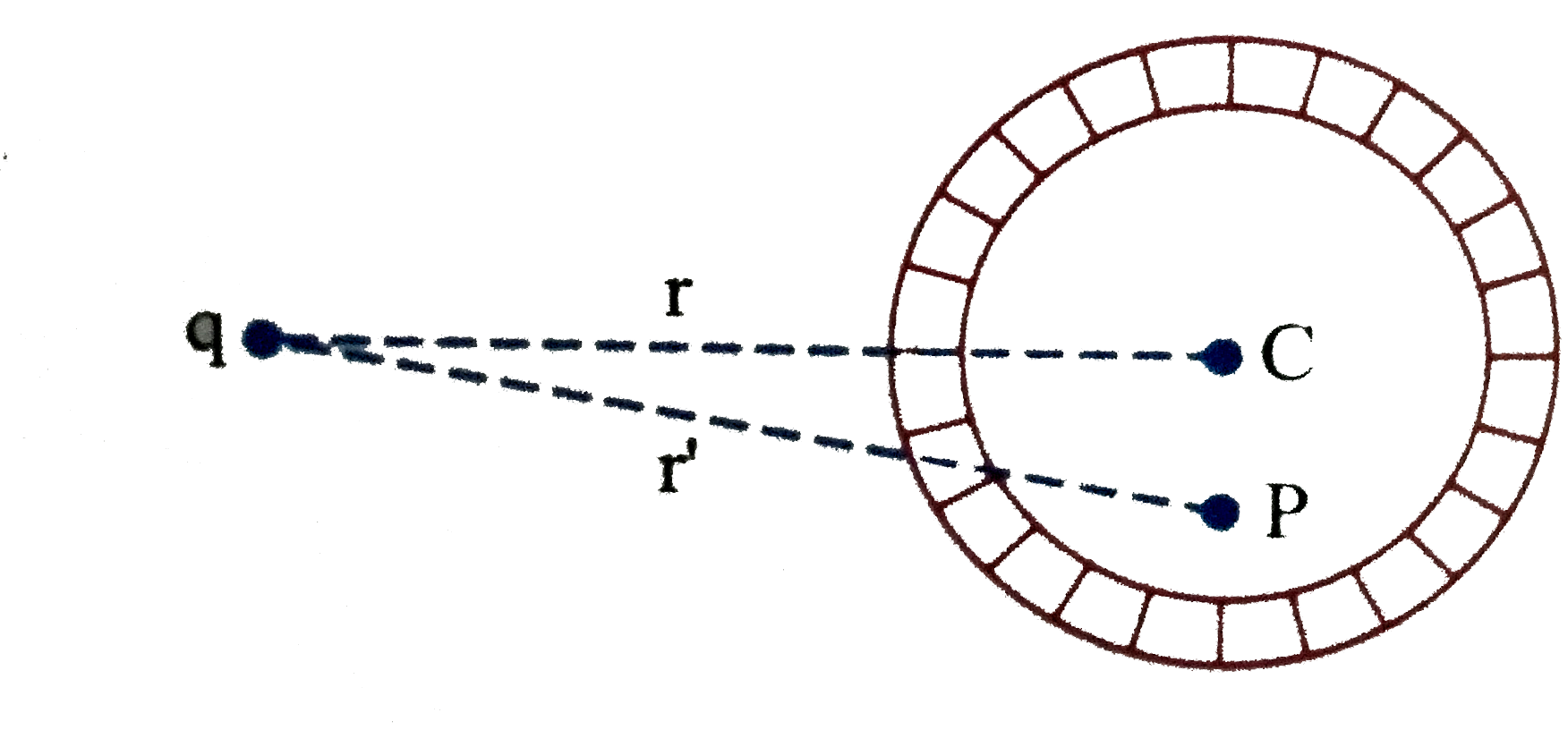
View SolutionA neutral conducting spherical shell is kept near a charge q as shown .The potentilal at point P due to the induced charge is
View SolutionA solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(b>a). The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as Vb. After taking these readings, he decides . to put charge of −4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is △V .
He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q2. He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q3.
q2 is
View SolutionA solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(b>a). The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as Vb. After taking these readings, he decides . to put charge of −4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is △V .
He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q2. He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q3.
Potential difference (△CV) measured by the student between the inner solid shere and outer shell after putting a charge −4Q is
View SolutionA solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(b>a). The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as Vb. After taking these readings, he decides . to put charge of −4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is △V .
He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q2. He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q3.
q3 is
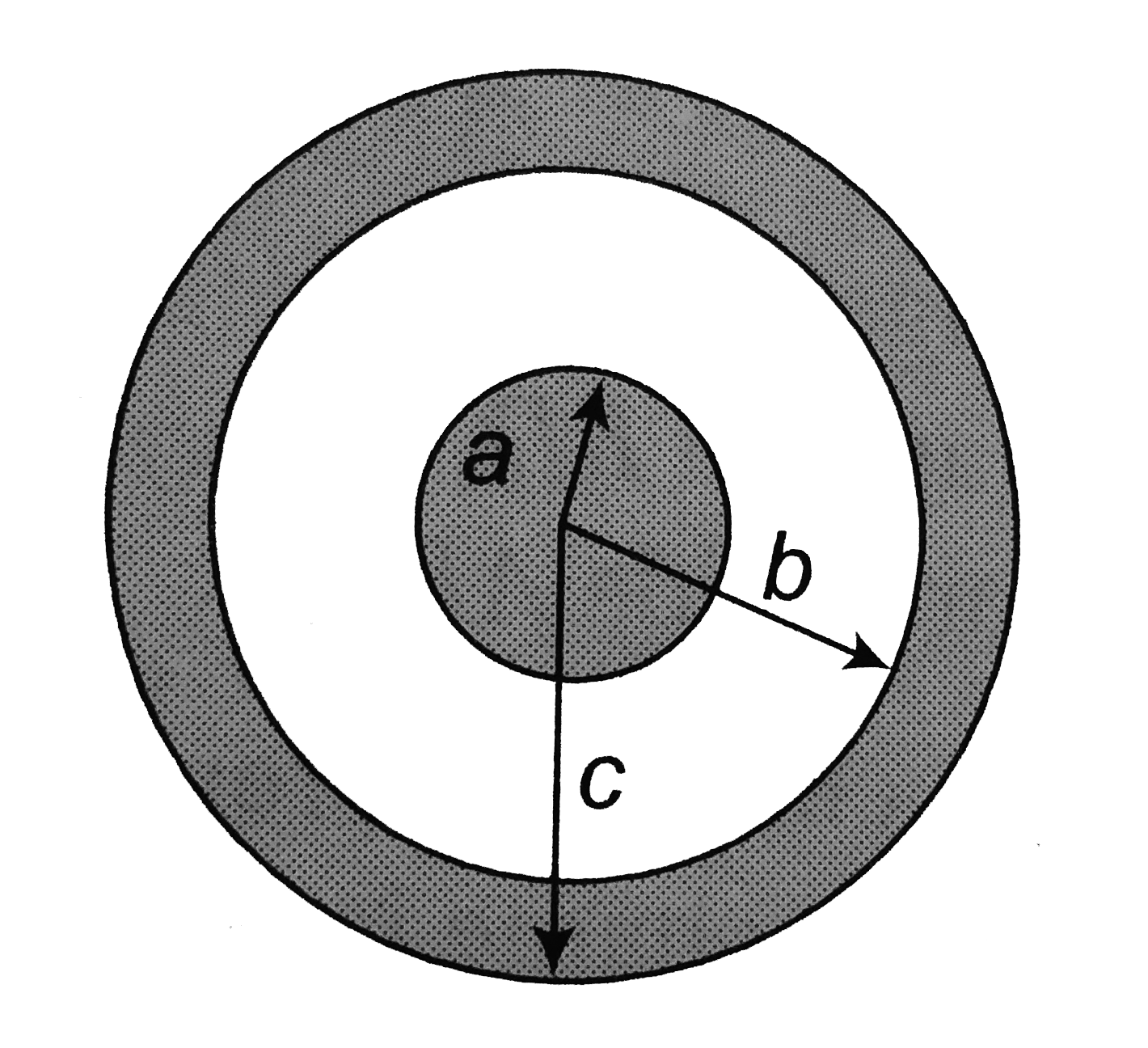
View SolutionA solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
View SolutionA point charge q is brought slowly from infinity and is placed at the centre of a conducting neutral spherical shell of inner radius a and outer radius b, then find work done by external agent :

View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View Solution

