Statement I: Internal resistance of a battery is drawn parallel to a battery in electical circuit.
Statement II: Heat generated in a battery is due to internal resistance.
Statement I is True , Statement II is True , Statement II is a correct explanation for Statement I.
Statement I is True, Statement II is True , Statement II is NOT a correct explanation for statement I.
Statement I is True , Statement is False.
Statement I is False, Statement II is True.
The correct Answer is:D
To solve the given question, we need to analyze the two statements provided and determine their validity.
1. Understanding Statement I:
- Statement I claims that the internal resistance of a battery is drawn parallel to the battery in an electrical circuit.
- Analysis: In electrical circuits, the internal resistance of a battery is typically modeled as being in series with the battery itself. This is because the internal resistance affects the total voltage output of the battery when current flows through it. Therefore, this statement is incorrect.
2. Understanding Statement II:
- Statement II states that the heat generated in a battery is due to internal resistance.
- Analysis: According to Joule's law, the heat generated (or power dissipated) in a resistor due to current is given by the formula P=I2R, where I is the current and R is the resistance. In the case of a battery, the internal resistance causes energy to be dissipated as heat when current flows through it. Thus, this statement is correct.
3. Conclusion:
- Since Statement I is false and Statement II is true, the correct option is that Statement I is false and Statement II is true.
Final Answer:
The correct option is: Statement I is false and Statement II is true.
---
- Statement I claims that the internal resistance of a battery is drawn parallel to the battery in an electrical circuit.
- Analysis: In electrical circuits, the internal resistance of a battery is typically modeled as being in series with the battery itself. This is because the internal resistance affects the total voltage output of the battery when current flows through it. Therefore, this statement is incorrect.
- Statement II states that the heat generated in a battery is due to internal resistance.
- Analysis: According to Joule's law, the heat generated (or power dissipated) in a resistor due to current is given by the formula P=I2R, where I is the current and R is the resistance. In the case of a battery, the internal resistance causes energy to be dissipated as heat when current flows through it. Thus, this statement is correct.
- Since Statement I is false and Statement II is true, the correct option is that Statement I is false and Statement II is true.
The correct option is: Statement I is false and Statement II is true.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Comprehension
13 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Integer
5 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Multiple Correct
5 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
In fig. battery E is balanced on 55cm length of potentiometer wire but when a resistance of 10Ω is connected in parallel with the battery then it balances on 50cm length of the potentiometer wire then internal resistance r of the battery is:-
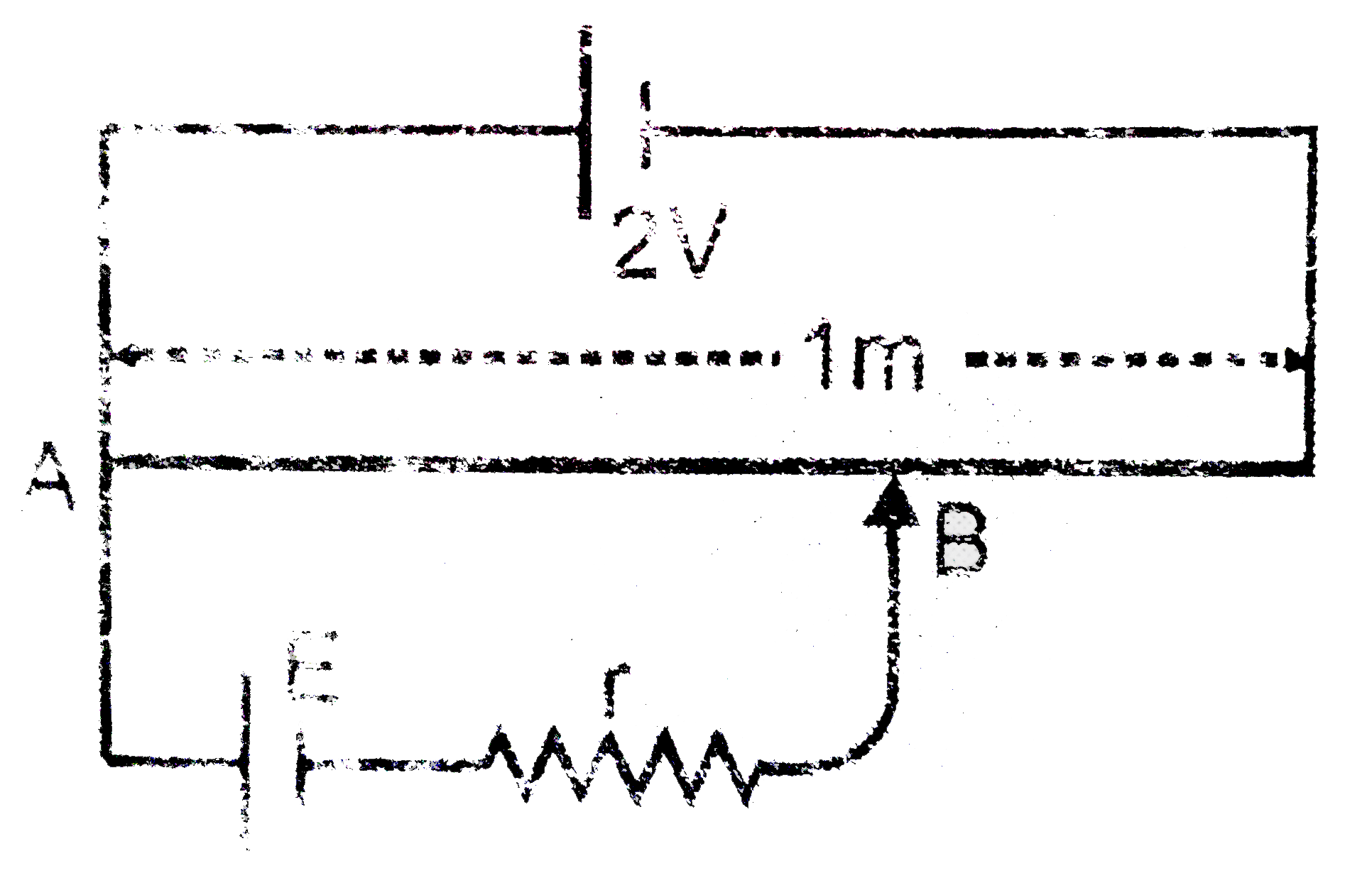
View SolutionFind the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure
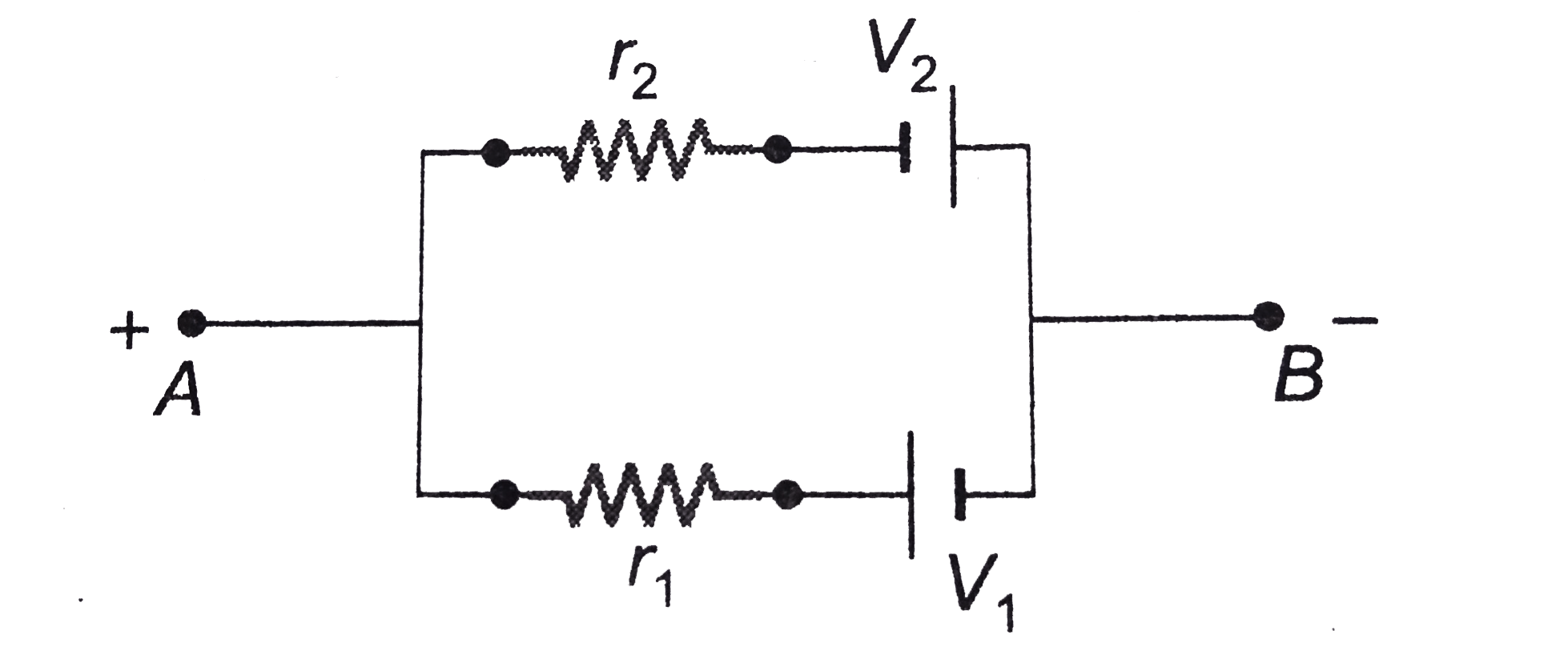
View SolutionFind the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure
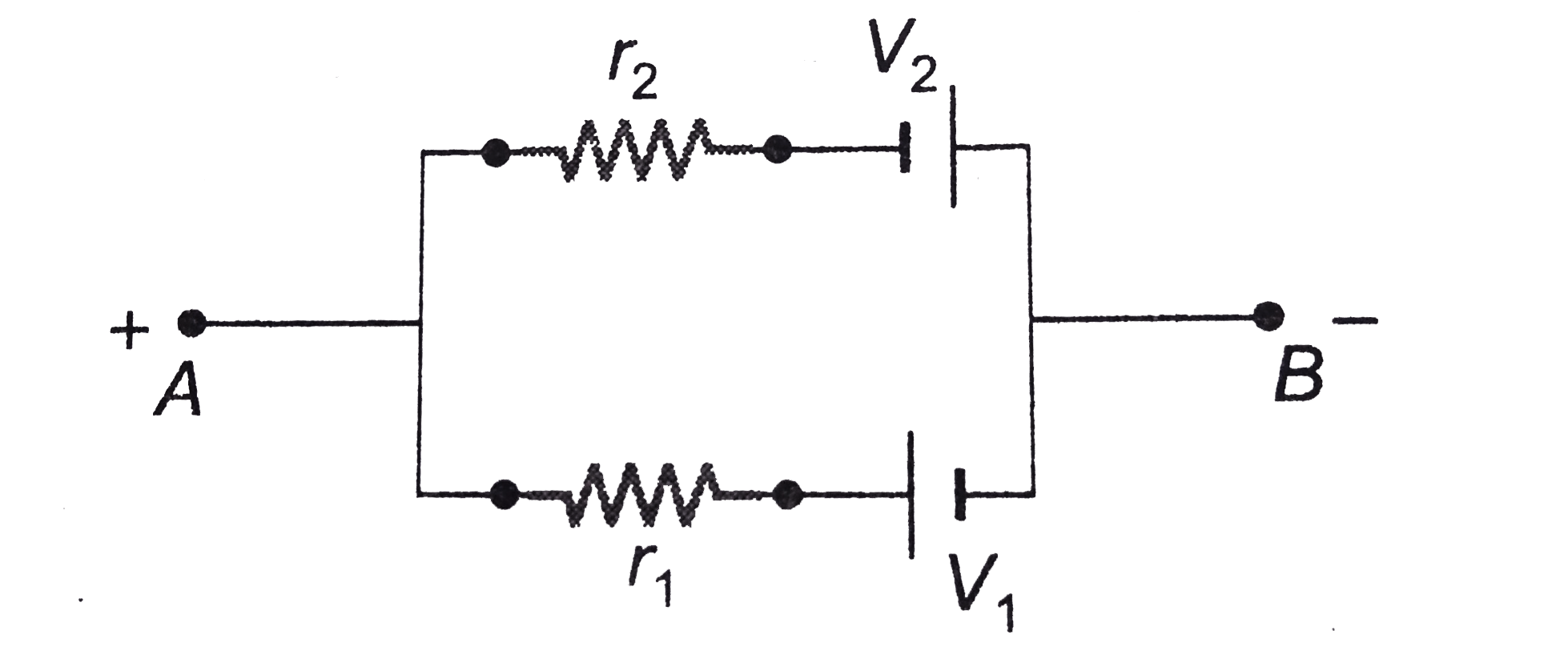
View Solutioncells each of emf e and internal resistance r are joined in series to form a row and such rows are connected in parallel to form a battery of N = mn cells. If this battery is connected to an external resistance R.
What is the emf of this battery and how much is its internal resistance ?
View Solutioncells each of emf e and internal resistance r are joined in series to form a row and such rows are connected in parallel to form a battery of N = mn cells. If this battery is connected to an external resistance R.
Show that current f flowing through the external resistance R is given by :
I=NemR+nr
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
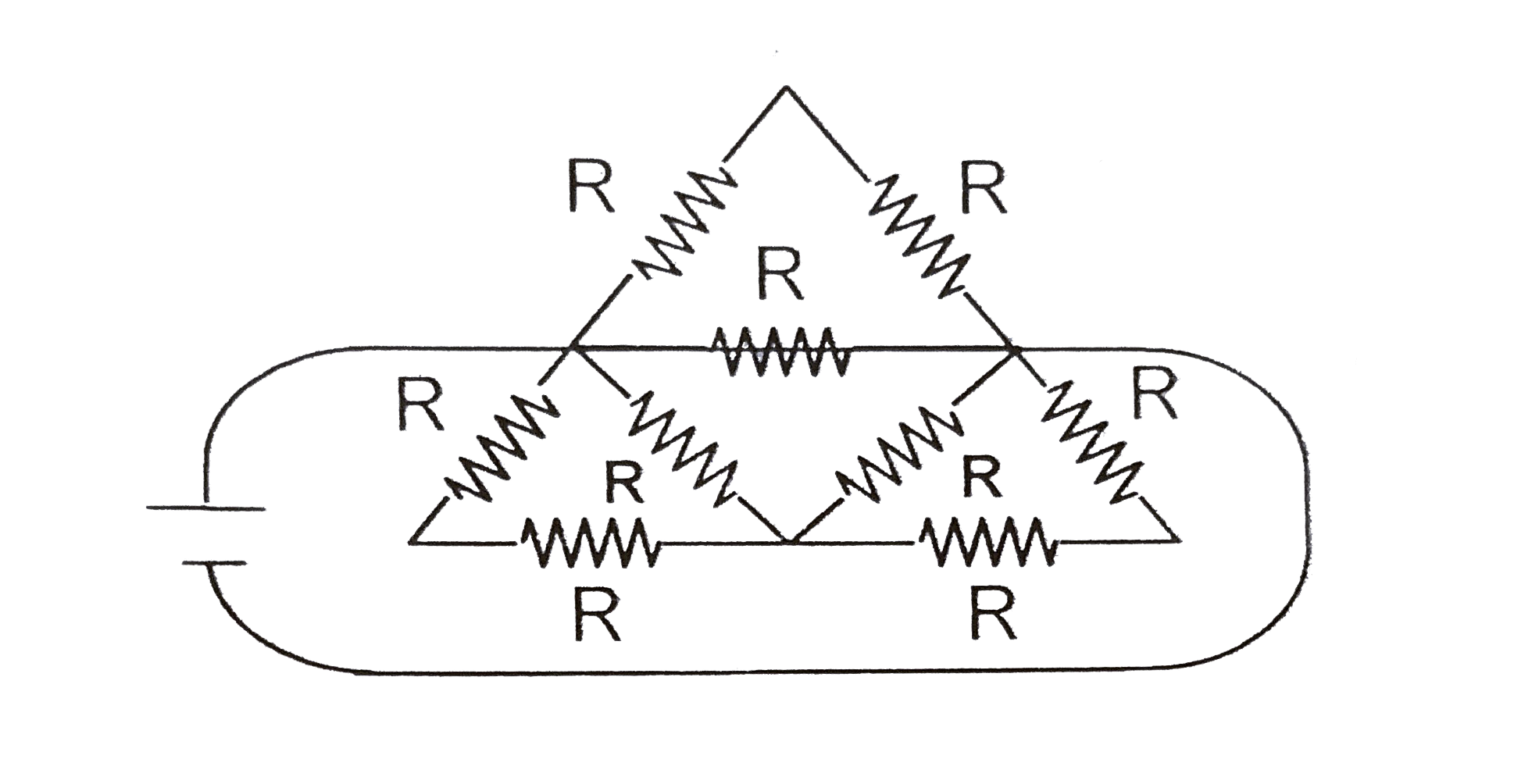
View SolutionFor maximum power from battery the internal resistance of battery r is
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View Solutionshows a circuit used in an experiment to detrmine the emf and interanl resistance of the battery C. A graph was plotted of the potential difference V between the terminals of the battery against the current I, which was varied by adjusting the rheostat. The graph is shown in x and y are the intercepts of the graph with the axes as shown. What is the internal resistance of the battery?
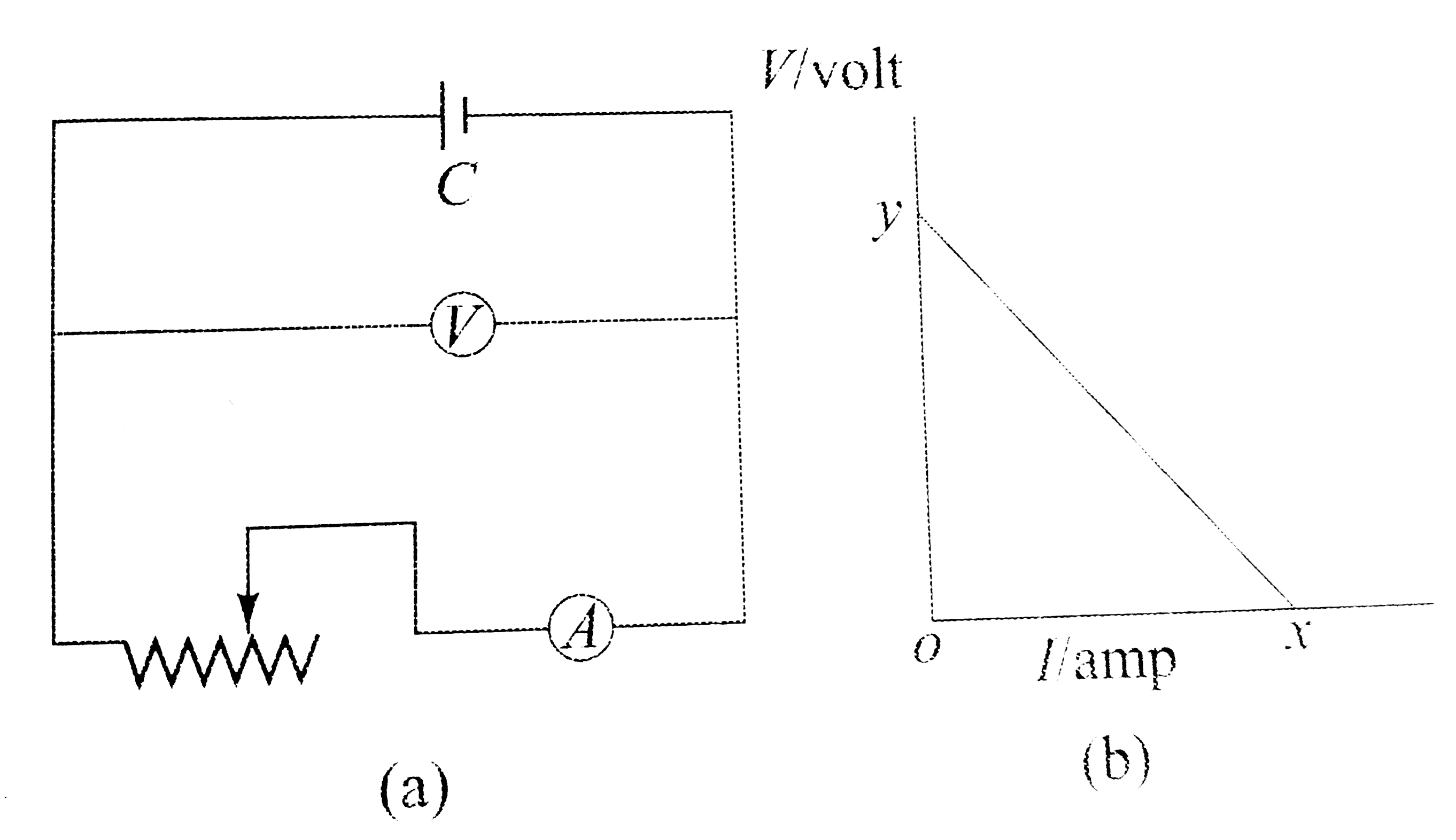
View Solutionn. cells, each of emf .e. and internal resistance .r. are joined in series to form a row. .m. such rows are connected in parallel to form a battery of N = mn cells. This battery is connected to an external resistance .R..
(i) What is the emf of this battery and how much is its internal resistance ?
Show that current .l. flowing through the external resistance .R. is given by-
I=NemR+nr
View Solution
