Statement I: The resistance of an ideal voltmeter should be infinite.
Statement II: Lower resistance of voltmeters gives a reading lower than the actual potential difference across the terminals.
Statement is true, Statement is True , Statement is correct explanation for Statement .
Statement is True, Statement is True, Statement is NOT a correct explantion for Statement .
Statement is True, Statement is False.
Statement is False, Satement is True.
The correct Answer is:A
To analyze the given statements, we will break down the concepts of voltmeters, their resistance, and how they affect the readings of potential difference.
Step 1: Understanding the Ideal Voltmeter
- An ideal voltmeter is designed to measure the potential difference (voltage) across two points in a circuit without affecting the circuit itself.
- For a voltmeter to not draw any current from the circuit, its resistance must be infinite.
Step 2: Analyzing Statement I
- Statement I claims that the resistance of an ideal voltmeter should be infinite.
- If the resistance is infinite, then no current flows through the voltmeter, which means it does not affect the circuit. Therefore, this statement is true.
Step 3: Analyzing Statement II
- Statement II states that a lower resistance of voltmeters gives a reading lower than the actual potential difference across the terminals.
- When a voltmeter with lower resistance is connected across a circuit, it draws some current. This current causes a voltage drop across the voltmeter itself, leading to a reading that is less than the actual voltage across the terminals.
Step 4: Comparing the Two Statements
- Since Statement I is true (the ideal voltmeter must have infinite resistance), and Statement II correctly explains why a voltmeter with lower resistance gives a lower reading, we can conclude that both statements are true.
- Moreover, Statement II serves as a correct explanation for Statement I.
Step 5: Conclusion
- Both statements are true, and Statement II is the correct explanation for Statement I. Therefore, the answer is that both statements are correct.
Final Answer:
Both Statement I and Statement II are true, with Statement II being the correct explanation for Statement I.
---
- An ideal voltmeter is designed to measure the potential difference (voltage) across two points in a circuit without affecting the circuit itself.
- For a voltmeter to not draw any current from the circuit, its resistance must be infinite.
- Statement I claims that the resistance of an ideal voltmeter should be infinite.
- If the resistance is infinite, then no current flows through the voltmeter, which means it does not affect the circuit. Therefore, this statement is true.
- Statement II states that a lower resistance of voltmeters gives a reading lower than the actual potential difference across the terminals.
- When a voltmeter with lower resistance is connected across a circuit, it draws some current. This current causes a voltage drop across the voltmeter itself, leading to a reading that is less than the actual voltage across the terminals.
- Since Statement I is true (the ideal voltmeter must have infinite resistance), and Statement II correctly explains why a voltmeter with lower resistance gives a lower reading, we can conclude that both statements are true.
- Moreover, Statement II serves as a correct explanation for Statement I.
- Both statements are true, and Statement II is the correct explanation for Statement I. Therefore, the answer is that both statements are correct.
Both Statement I and Statement II are true, with Statement II being the correct explanation for Statement I.
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Comprehansion
15 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Integer
8 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Multiple Correct
7 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type
7 Videos
Similar Questions
Knowledge Check
A voltmeter having a resistance of 1800Ω employed to measure the potential difference across a 200Ω resistor which is connected to the terminals of a dc power supply having an emf of 50 V and an internal resistance of 20Ω. What is the percentage decrease in the potential difference across the 200Ω resistor as a result of connecting the voltmeter across it?
A1%B5%C10%D25%
If the reading of the ideal voltmeter shown in the circuit is 2V the internal resistance of the two identical cells is
_2019_CBT5_E01_030_Q01.png)
View SolutionA battery of emf 1.4V and internal resistance 2Ω is connected to a resistor of 100ω resistance through an ammeter. This resistance of the ammeter is 4/3Ω. A voltmeter has also been connected to find the potential difference across the resistor.
a. Draw the circuit diagram.
b. The ammeter reads 0.02A. What is the resistance of the voltmeter?
c. The voltmeter reads 1.1V. What is the error in the reading?
View SolutionIn the given circuit, the reading of ideal voltmeter is E/2. The internal resistance of the battery is
View Solution(A) : The resistance of voltmeter is very small as compared to the resistance of the galvanometer, from which it is obtained.
(R) : The voltmeter is connected in series to the conductor across which potential difference is to be measured.
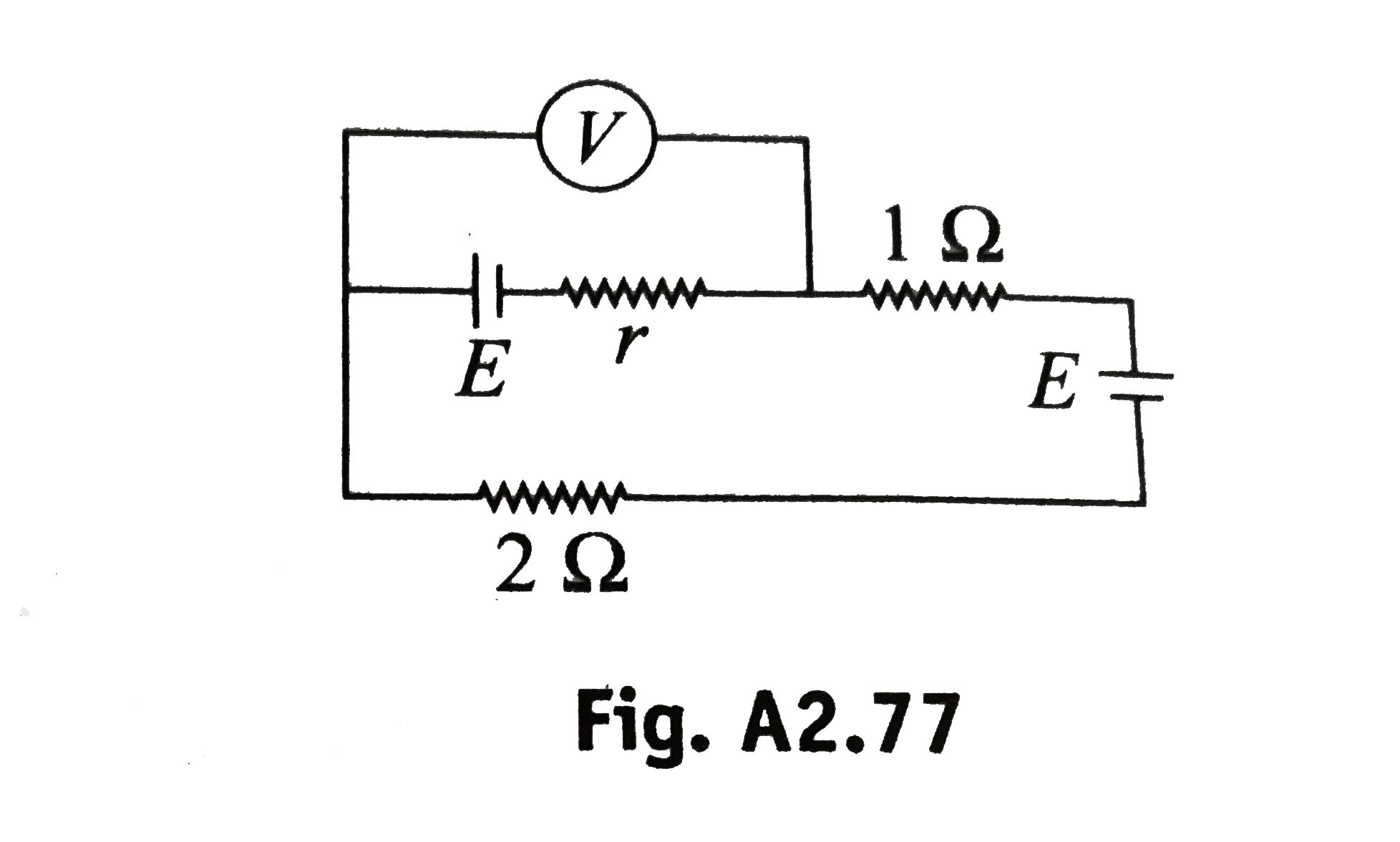
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
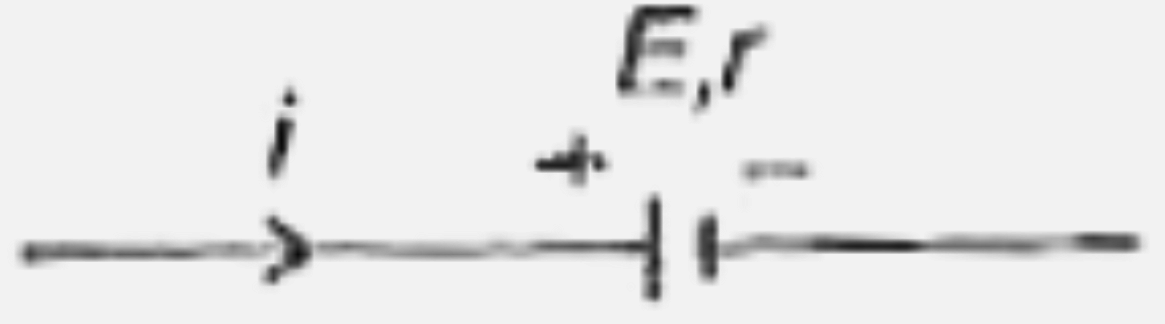
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionA voltmeter and an ammeter are connected in series to an ideal cell of emfE. The voltmeter reading is V, and the ammeter readings is I. Then
(i) V<E (ii) the voltmeter resistance is V/I
(iii) the potential difference across the ammeter is E−V
(iv) Voltmeter resistance + ammeter resistance = E//I
Correct statements are
View Solution
