Consider 12 resistor arranged symmetrically in shape of bipyraimd ABCDEF. Here ABCD is a square. Point E, point F, and centre of square are in the same straight line perpendicular to the planw of squar. The resistacne of each resistor is R.

The effective resistance between A and B is
none of these
The correct Answer is:C
If we cannot battery between E and F, then A, B, C, and D will be
all at the same potential. 
If we connect a battery
between A and C, then E and
F will be at the same potential.
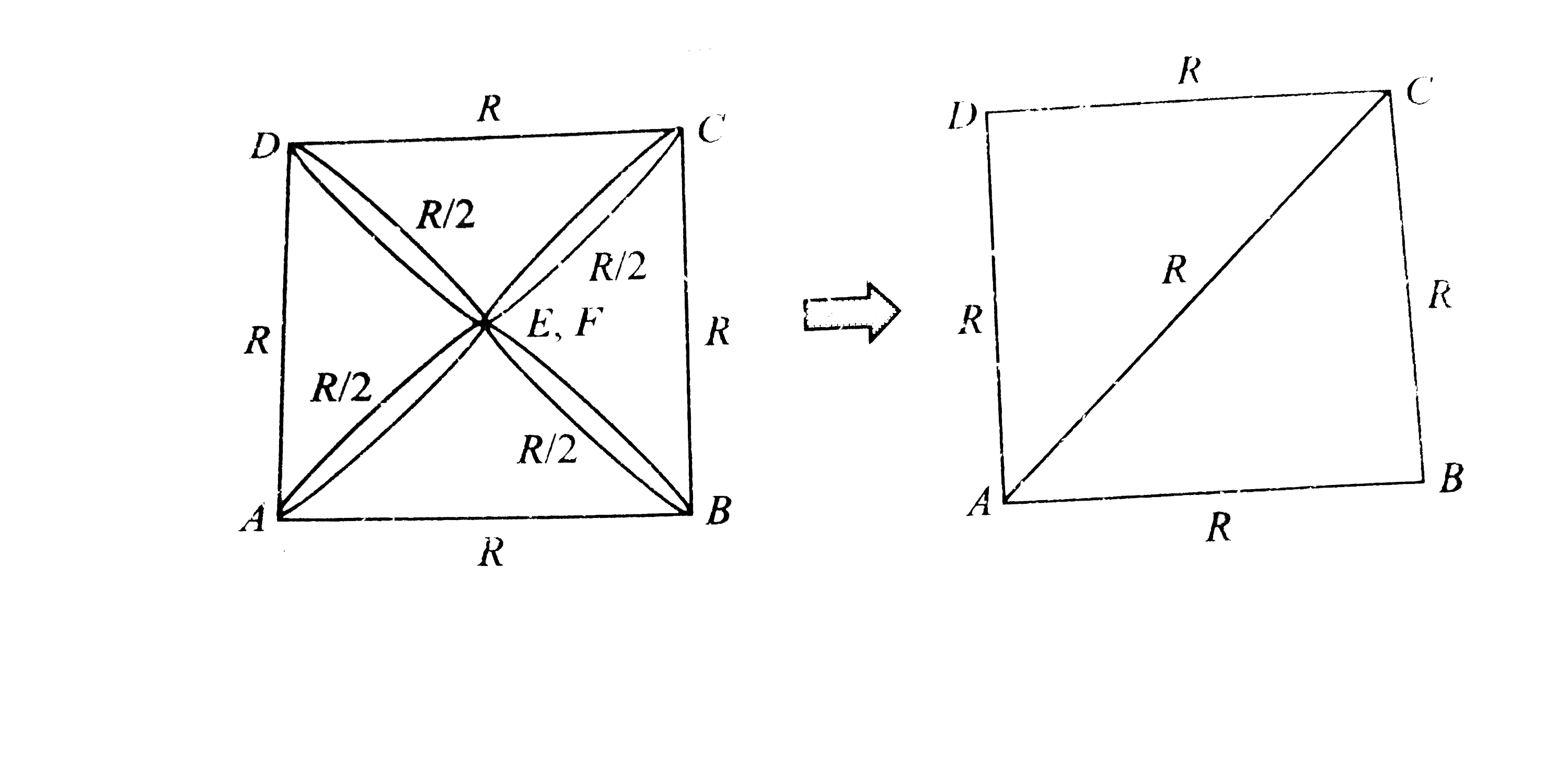 ,
, 
Now resistance between DE and EB will be useless. Thus,
Let us remove the resistance between A and B, then E and F will be at
the same potential, we can draw the remaining as follows:
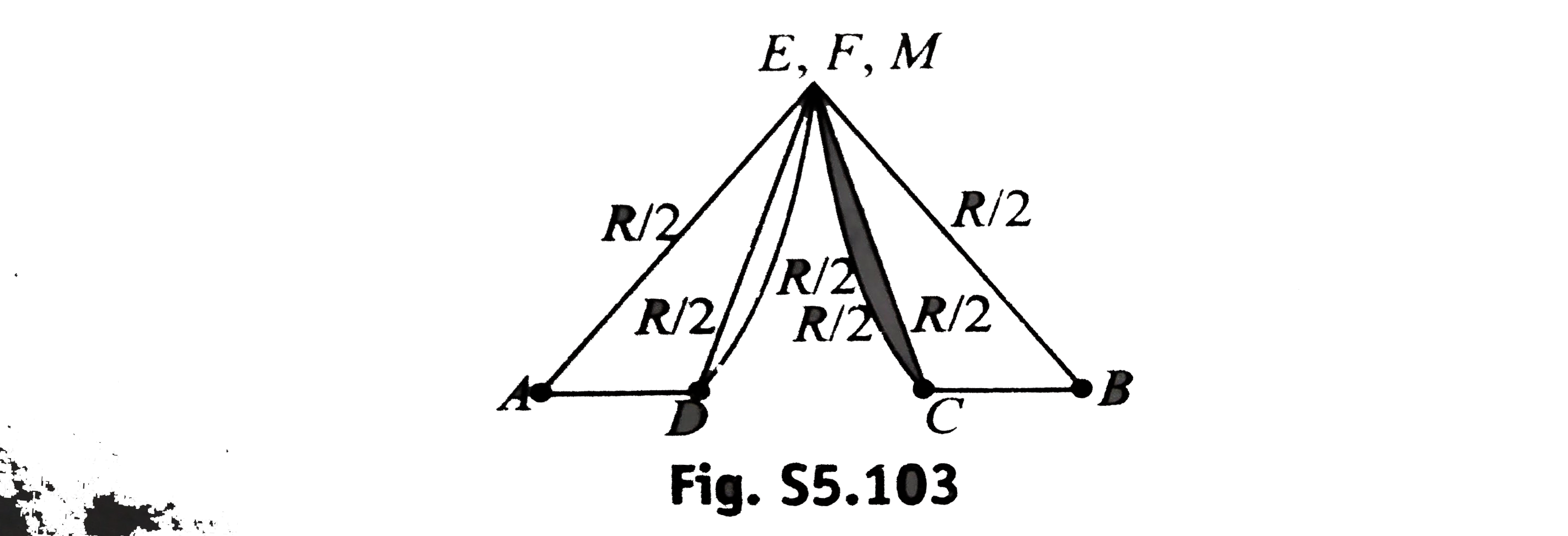 ,
,
M is the midpoint of DC, so M will be at the same spot as E and F.
Now find The resistance that we had removed will be in
parallel to it, so
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct
16 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
Consider 12 resistor arranged symmetrically in shape of bipyraimd ABCDEF. Here ABCD is a square. Point E, point F, and centre of square are in the same straight line perpendicular to the plane of square. The resistance of each resistor is R.

The effective resistance between A and C is
View SolutionConsider 12 resistor arranged symmetrically in shape of bipyramid ABCDEF. Here ABCD is a square. Point E, point F, and centre of square are in the same straight line perpendicular to the plane of squar. The resistance of each resistor is R.

The effective resistance between E and F is
View Solution
Knowledge Check
Five resistors are connected as shown in adjoining figure.
The effective resistance i.e., equivalent resistance between the points A and B is :
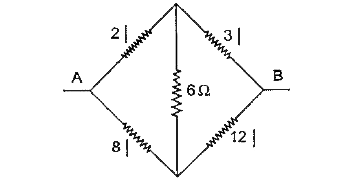 A4ΩB5ΩC15ΩD20Ω
A4ΩB5ΩC15ΩD20Ω
Each resistor shown in figure is an infinite network of resistance1Ω. The effective resistance Between points A and B is
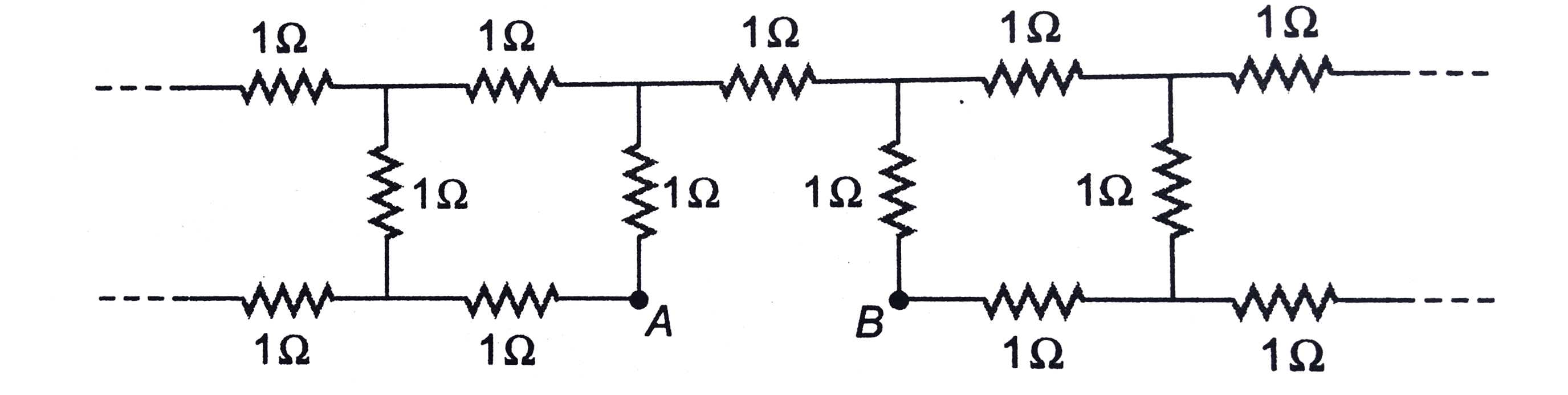
View SolutionIn the adjoining network of resistors, each is of resistance r ohm, the equivalent resistance between points A and B is–

View SolutionIn the shown wire frame, each side of a square (the smallest square) has a resistance R. The equivalent resistance of the circuit between the points A and B is

View SolutionFree resistors are connected as shown in adjoining figure.
The effective resistance i.e. quivalent resistance between the points A and B is :
View SolutionA write of resistance R is bent to form a square ABCD as shown in the figure. The effective resistance between E and C is :
(E is mid-point of arm CD)

View SolutionInfinite square brackets have been made by a infinitely long wire as shown. Between each junction, the resistance is r. Find equivalent resistance between points a and b
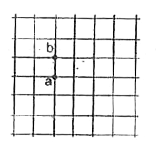
View SolutionFind the equivalent resistance of the circuits shown in figure between the points a and b. Each resistor has a resistance r.


View Solution
