Potential difference across the terminals of a cell was measured (in volts) against different current (in ampere) flowing through the cell. A graph was drawn, which was a straight line ABC. Using the data given in the graph determine
a. the emf, and
b. the internal resistance of the cell.
To solve the problem, we will follow the steps outlined in the video transcript. We will determine the electromotive force (emf) and the internal resistance of the cell using the relationship between potential difference (V), emf (E), and internal resistance (r).
1. Understanding the Relationship:
The relationship between the potential difference (V), emf (E), and internal resistance (r) is given by the formula:
V=E−I⋅r
where:
- V is the potential difference across the terminals of the cell,
- E is the emf of the cell,
- I is the current flowing through the cell,
- r is the internal resistance of the cell.
2. Finding the EMF (E):
From the graph, we identify the point where the current (I) is zero. At this point, the potential difference (V) is equal to the emf (E) because there is no current flowing and thus no voltage drop across the internal resistance.
- According to the transcript, when I=0, V=1.4V.
- Therefore, we can conclude that:
E=1.4V
3. Finding the Internal Resistance (r):
Next, we need to find the internal resistance of the cell. We can use another point from the graph where the potential difference is zero.
- According to the transcript, when V=0V, the current I=0.28A.
- We can substitute these values into the equation:
0=E−I⋅r
Rearranging gives us:
E=I⋅r
Substituting the known values:
1.4=0.28⋅r
To find r, we divide both sides by 0.28:
r=1.40.28=5Ω
Final Results:
- The emf of the cell E is 1.4V.
- The internal resistance r of the cell is 5Ω.
The relationship between the potential difference (V), emf (E), and internal resistance (r) is given by the formula:
V=E−I⋅r
where:
- V is the potential difference across the terminals of the cell,
- E is the emf of the cell,
- I is the current flowing through the cell,
- r is the internal resistance of the cell.
From the graph, we identify the point where the current (I) is zero. At this point, the potential difference (V) is equal to the emf (E) because there is no current flowing and thus no voltage drop across the internal resistance.
- According to the transcript, when I=0, V=1.4V.
- Therefore, we can conclude that:
E=1.4V
Next, we need to find the internal resistance of the cell. We can use another point from the graph where the potential difference is zero.
- According to the transcript, when V=0V, the current I=0.28A.
- We can substitute these values into the equation:
0=E−I⋅r
Rearranging gives us:
E=I⋅r
Substituting the known values:
1.4=0.28⋅r
To find r, we divide both sides by 0.28:
r=1.40.28=5Ω
- The emf of the cell E is 1.4V.
- The internal resistance r of the cell is 5Ω.
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective
29 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Single Correct
72 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.1
28 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
Potential difference across terminal sof a cell were measured ( in volts) against different currents ( in ampere) flowing through cell. A graph ABC is drawn as shown. Determine
(a) The emf.
(b) Internal resistance of cell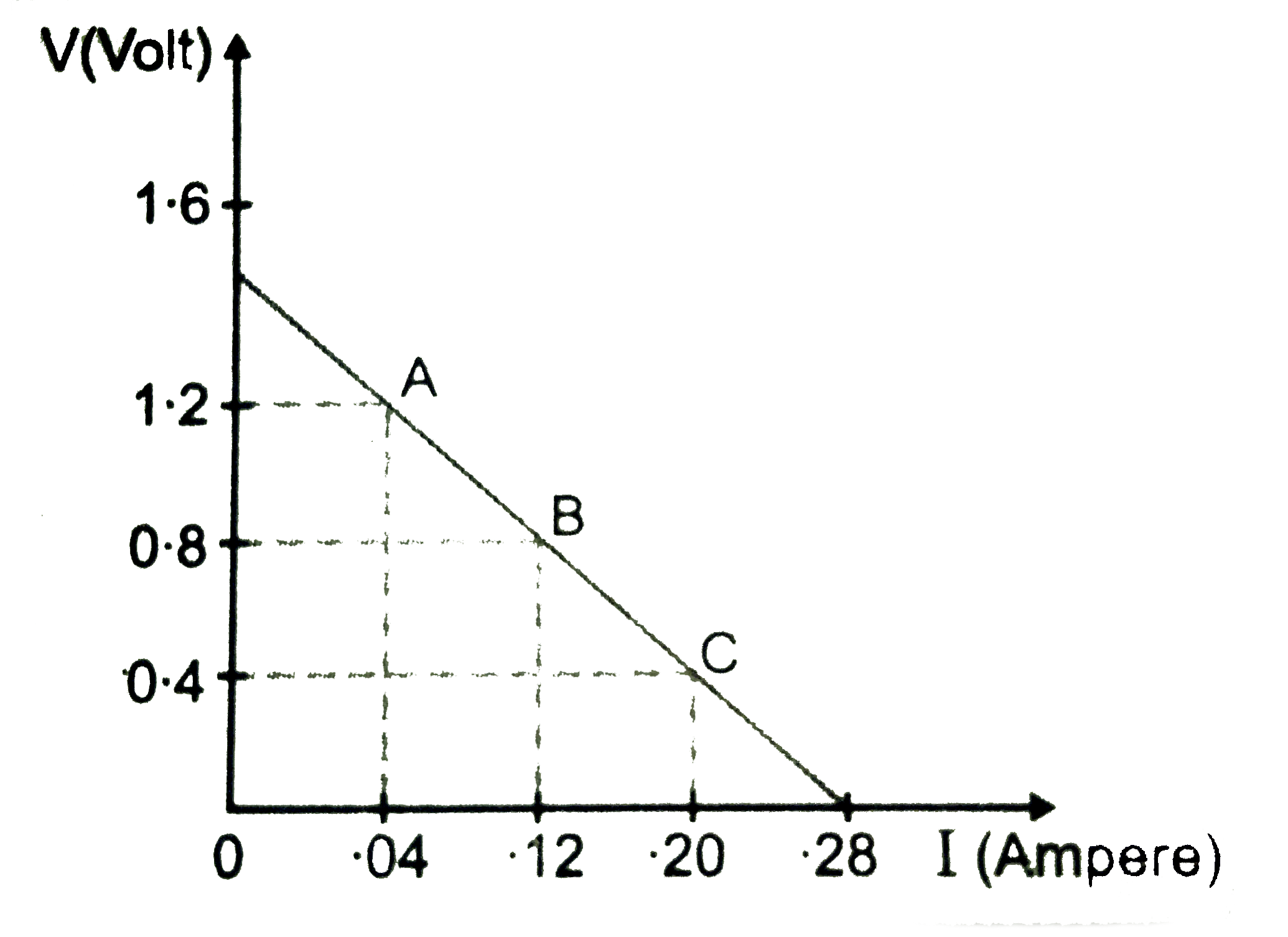
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
View SolutionA cell of emf E is connected across a resistance R. The potential difference between the terminals of the cell is found to be V. The internal resistance of the cell must be -
View SolutionWhat is the relationship between potential difference across the terminals of a cell and emf of the cell ?
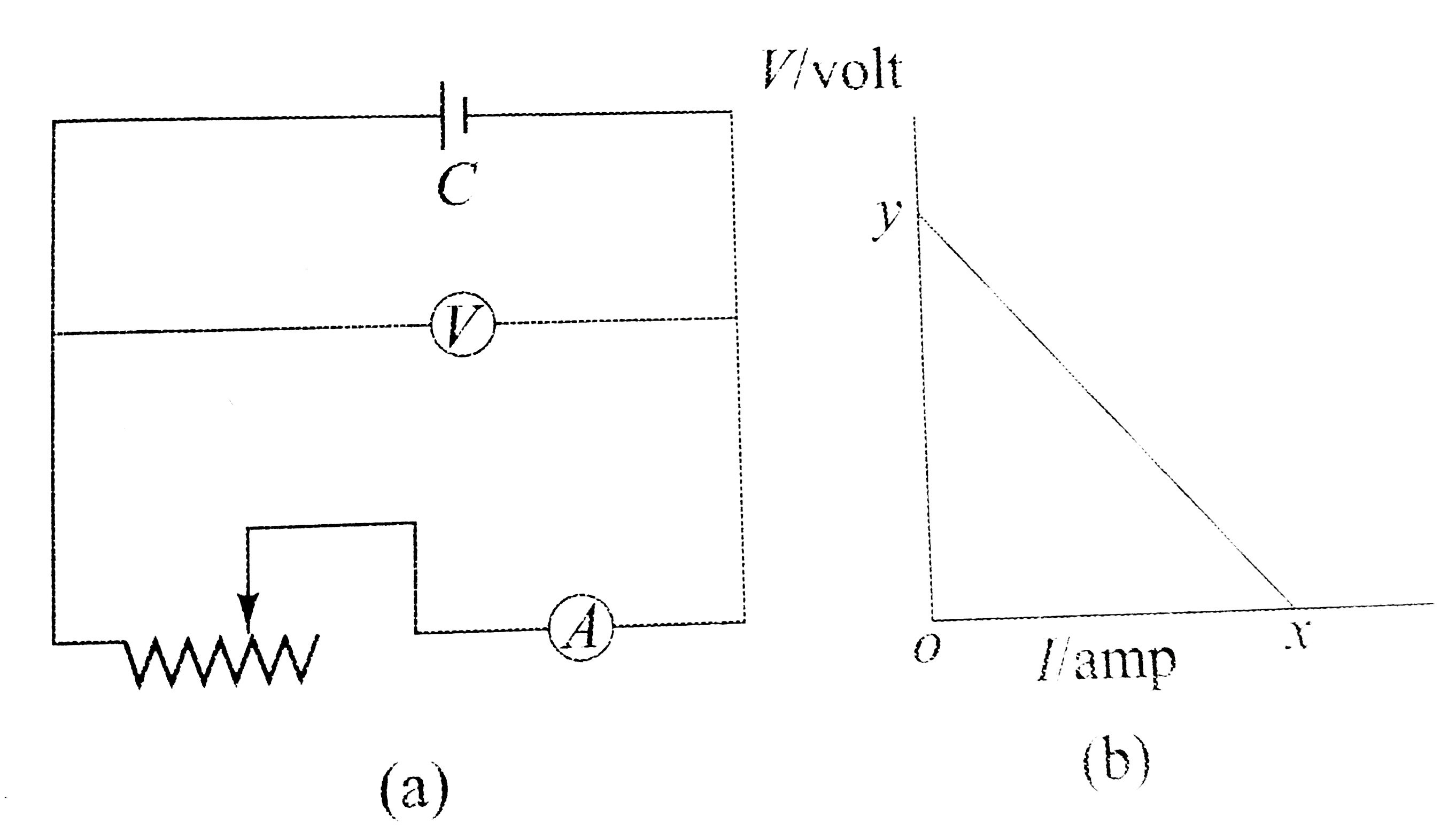
View Solutionshows a circuit used in an experiment to detrmine the emf and interanl resistance of the battery C. A graph was plotted of the potential difference V between the terminals of the battery against the current I, which was varied by adjusting the rheostat. The graph is shown in x and y are the intercepts of the graph with the axes as shown. What is the internal resistance of the battery?
View SolutionThe potential difference across the terminals of a battery is 8.4V when there is a current of 1.50A in the battery from the negative to the positive terminal. When the current is 3.50Air, the reverse direction, the potential difference becomes 9.4V.
(a) What is the internal resistance of the battery?
(b) What is the emf of the battery?
View SolutionThe figure shows a plot of terminal voltage 'V' verus the current 'I' of a given cell. Calculate from the graph (a) emf of the cell and (b) internal resistance of the cell.

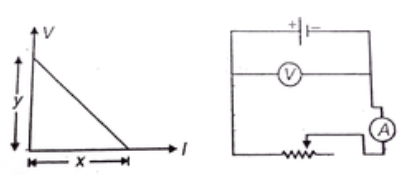
View SolutionFor the determination of emf E and internal resistance 'r' of a cell , the graph is obtained between potential difference V between the terminal of the cell against the current l, which was changed by adjusting the rheostat, is as shown . The internal resistance of the cell is
View SolutionFor a cell, the graph between the potential difference (V) across the terminals of the cells and the current I drawn from the cell is as shown in figure. Calculate the e.m.f. and the internal resistance of the cell.

View SolutionA cell has an emf 1.5V. When connected across an external resistance of 2Ω, the terminal potential difference falls to 1.0V. The internal resistance of the cell is:
View Solution
