Twelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in figure.

Video Solution
Text Solution
Let us assume we have
connected a battery of emf V
across points 1 and 6. if potential
of point 1 is V, then the potential
of point 6 is 0.
From symmetry, it is clear that
the current entering at point1 will equally divide the resistance. Hence, the potential differences
across resistances, conncted
across (1,8) , (1,2), and (1,4), will be equal .
Similarly the current coming out at point 6 will be equal
to current ennering at point 1. By symmetry, we can say the current in the resistances connected across points (7,6),
(3,6), and (6,5) will be equal. Hence, potential difference
across these resistance should be equal. Let us assume the
potentials at points 3,5, and 7 be x then the potentials at points 2,4, and 8 should be (V - x). At point 7,
[x−(V−x)]R+x−0R+[x−(V−x)]R=0
or x25V(i)
At point 1, I=3[V−(V−x)]R=3xR(ii)
From (i) and (ii)
VI=5R6
Hence, effective resistance will be 5R/6.

|
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples
12 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.1
28 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
Knowledge Check
The equivalent resistance between A and B for . the circuit shown in this figure is
 A13.1ΩB15.1ΩC17.1ΩD19.1Ω
A13.1ΩB15.1ΩC17.1ΩD19.1Ω
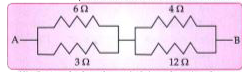
Find the equivalent resistance between A and B in the given figure.

View SolutionFind the equivalent resistance between A and B in the give figure .
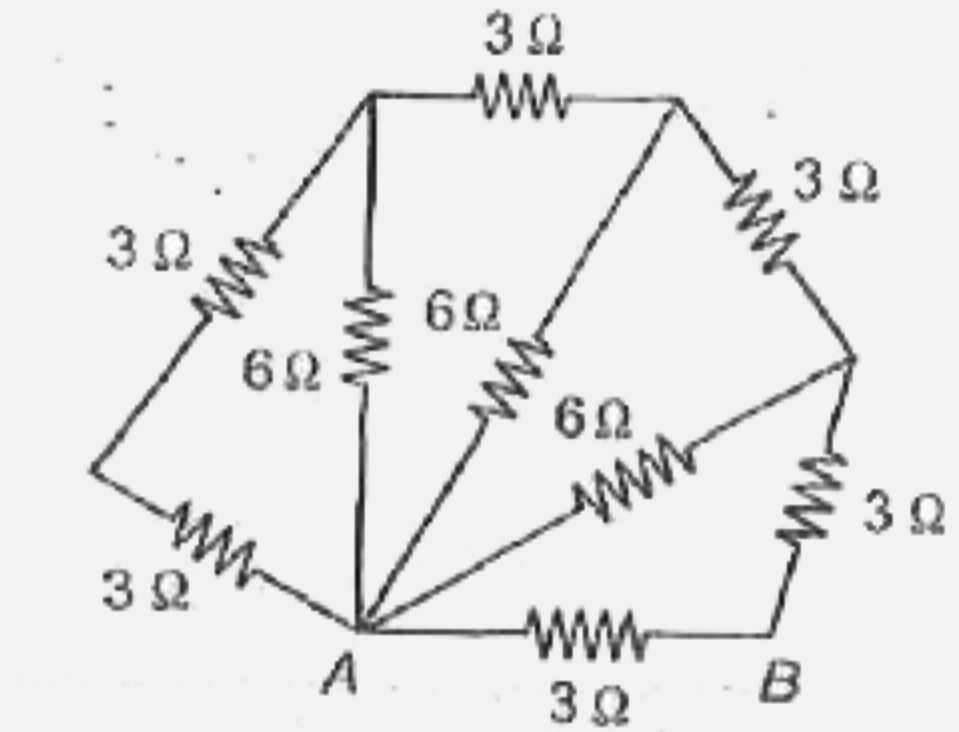
View SolutionThe equivalent resistance between points A and B in the circuit shown in figure is
_PHY_E05_095_Q01.png)
View SolutionThe equivalent resistance between point A and B in the circuit shown in figure is
_PHY_E05_041_Q01.png)
View SolutionIn the same figure, equivalent resistance between points A and D is
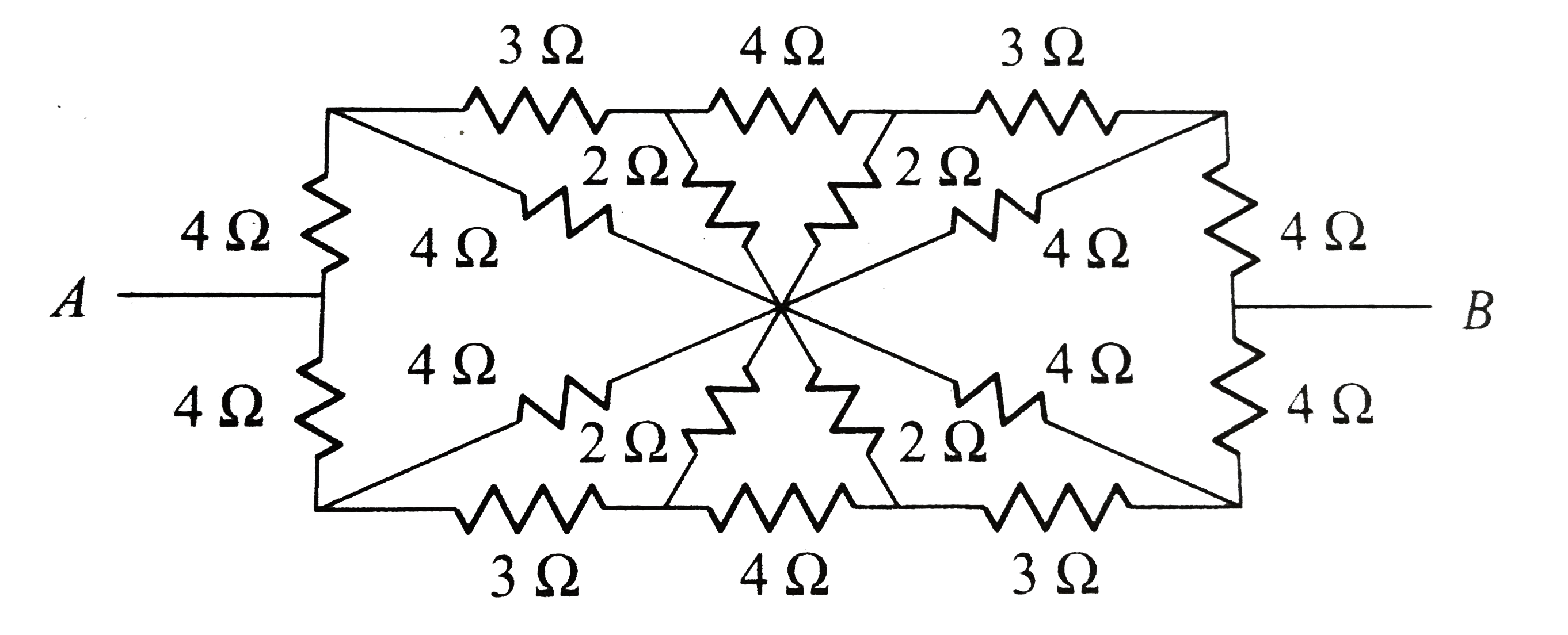
View SolutionA number of resistors are connected as shown in the figure. The equivalent resistance between A and B is
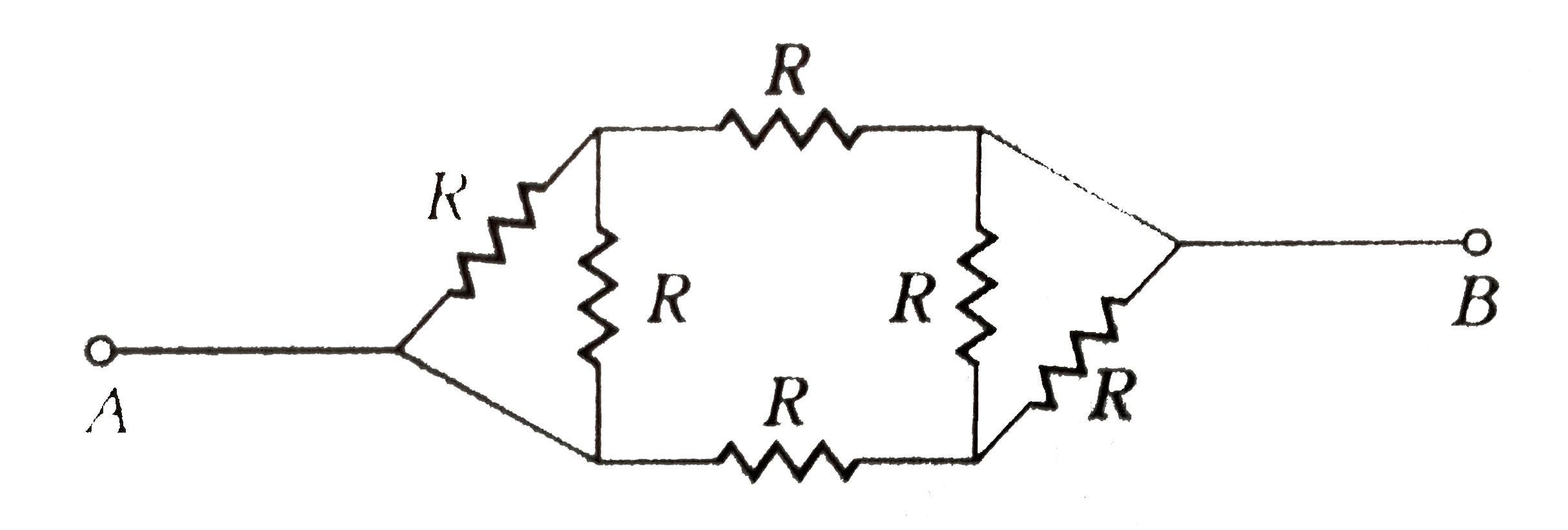
View SolutionThe equivalent resistance resistance between A and B of network shown in figure is
View Solution