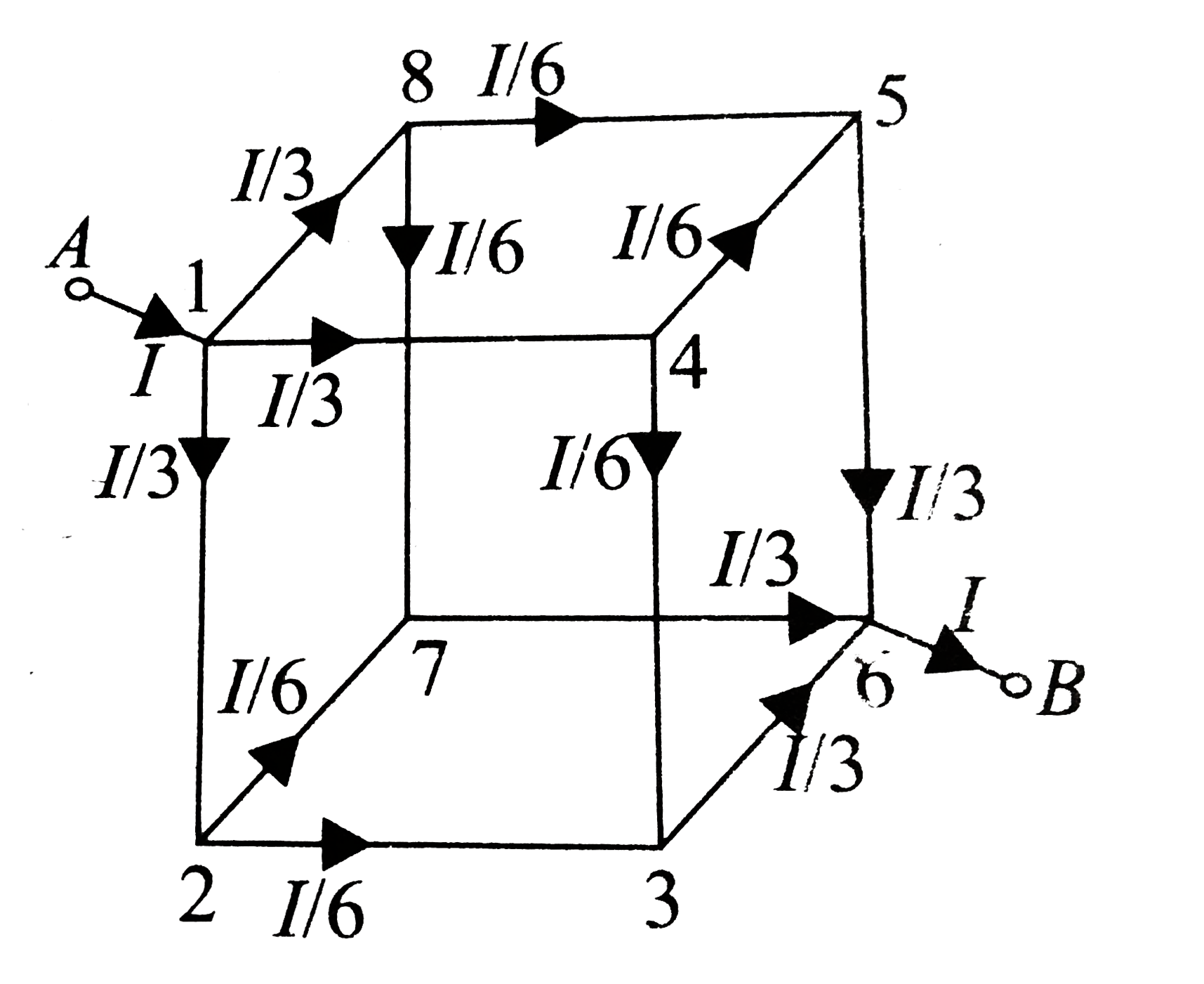
Twelve identical resistances arranged on all edges of a cube. The resisors are all the same. Then find the equivalent resistance between the edges A and B as shown in.

Video Solution
Text Solution
Let un number the corners as 1,2,3,…. As
shown in fig 5.46 Let us identify various paths from A to B
a(1−8−7−6),b(1−2−7−6),c(1−8−5−6),<br>d(1−2−3−6),e(1−4−5−6),f(1−4−3−6)
Now for each of these paths
we have identical resistances. Let
the current entering at point A be
I. The current will be distributed
equally among all the three paths.
therefore, we can say that current
is I12=I23=12(I3)=I6
Similarly, we can say that I43=I45=I85=I87=I/6. Therefore, to
calculate the potential difference across the paht (1→2→7→6),
we have
V1−I3R−I6R−I3R=V6
or V1V6=I[R3+R6+R3]=56IR
or(V1−V6)I=56R
Therefore, the equivalent resistance is 5R/6.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
Twelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in figure.
 View Solution
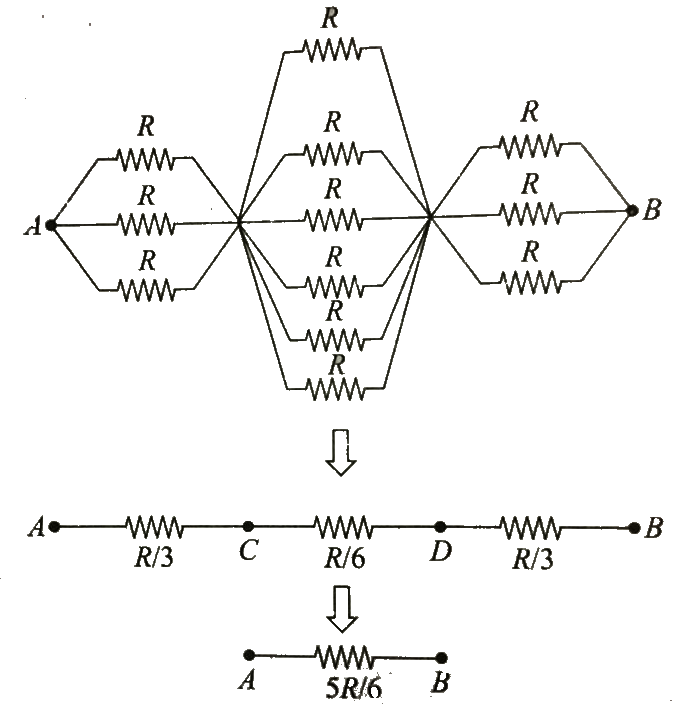
View SolutionFind the equivalent resistance between A and B
 View Solution
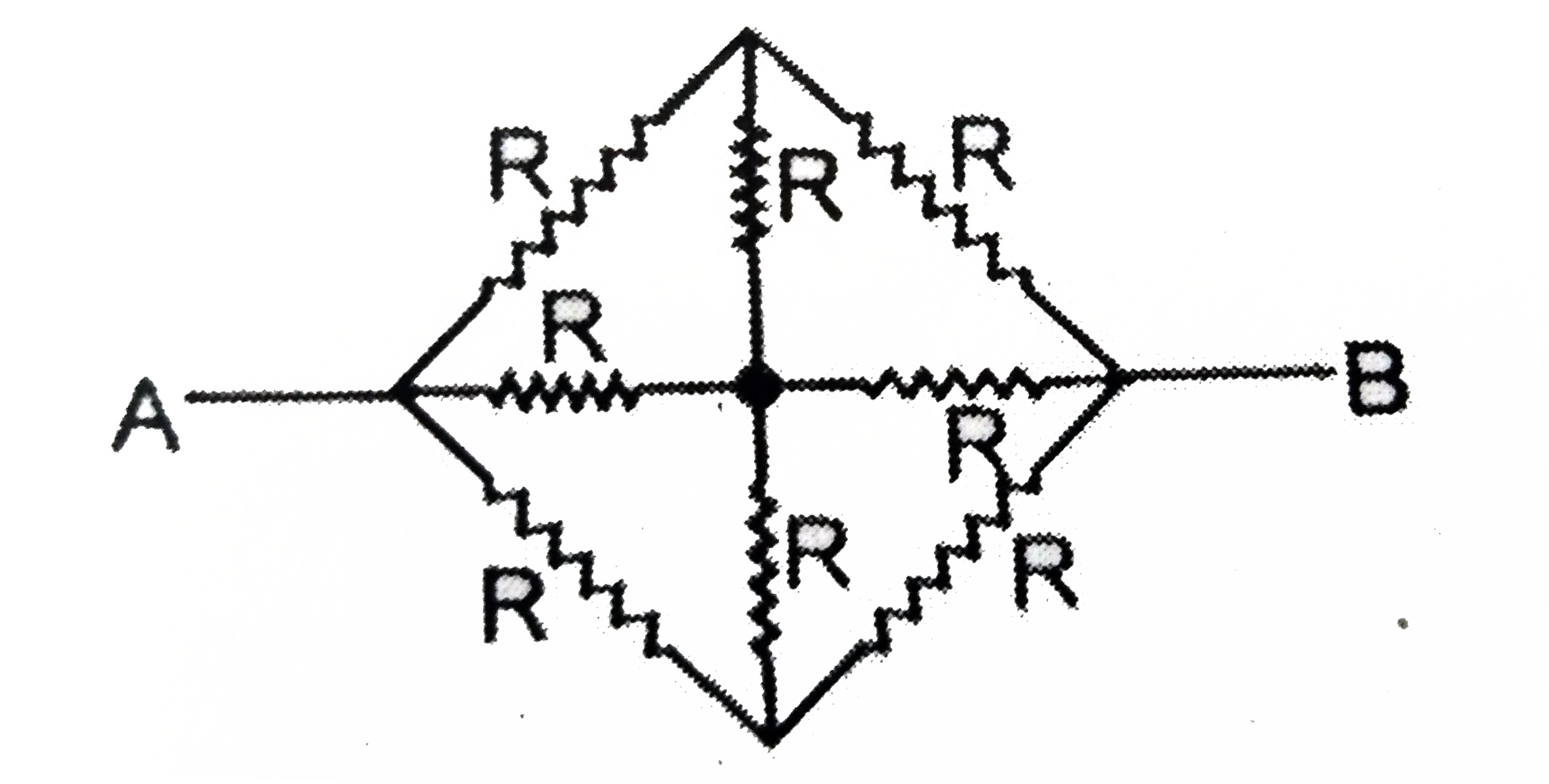
View SolutionFind the equivalent resistance between A and B
 View Solution
View Solutionfind the equivalent resistance between A and B.
 View Solution
View SolutionFind the equivalent resistance between points A and B
 View Solution
View SolutionFind the equivalent resistance between A and B.
 View Solution
View SolutionFind the equivalent resistance between A and B.
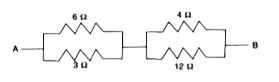 View Solution
View SolutionFind the equivalent resistance between A and B.

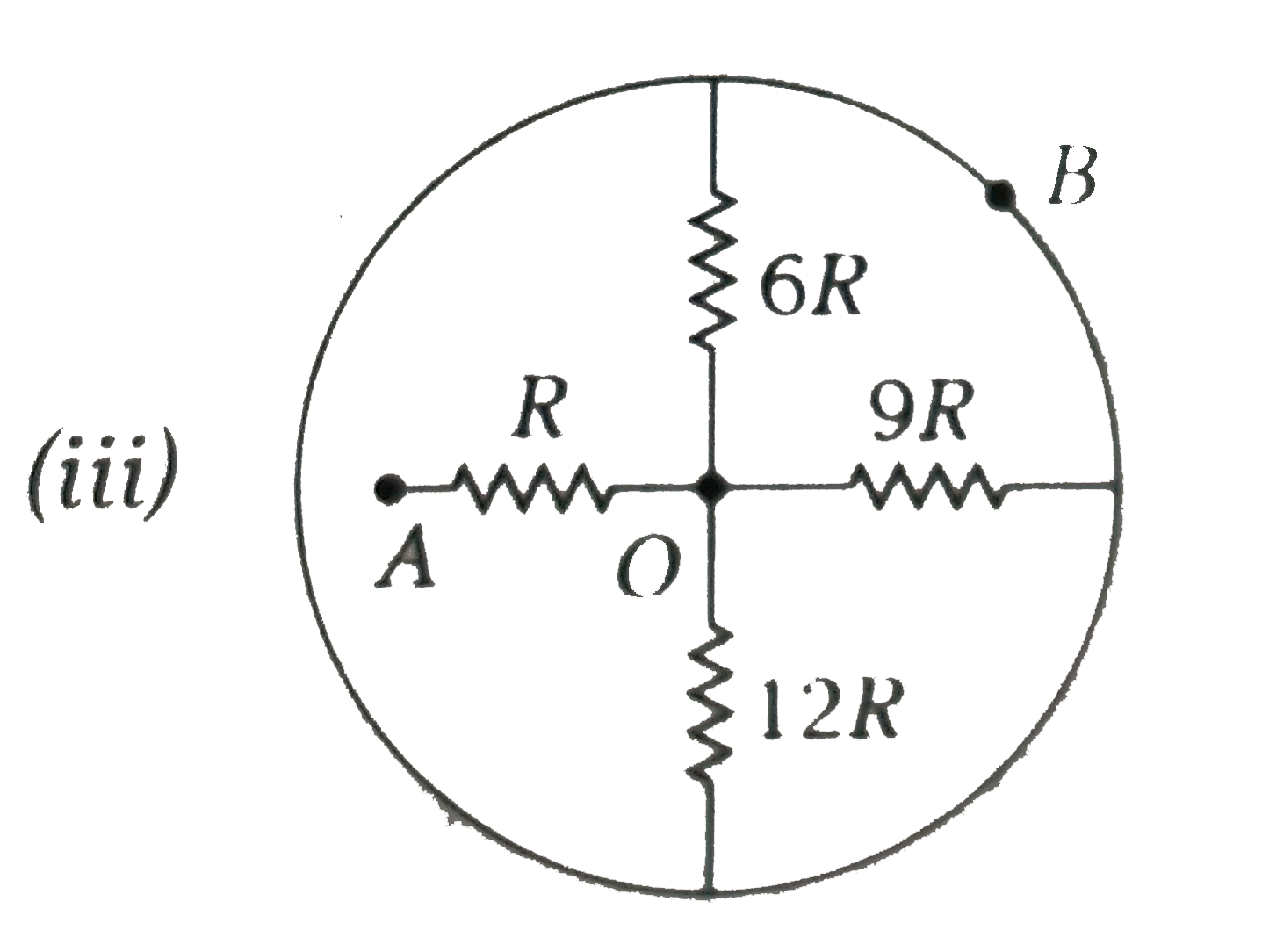 View Solution
View SolutionFind the equivalent resistance between A and B.
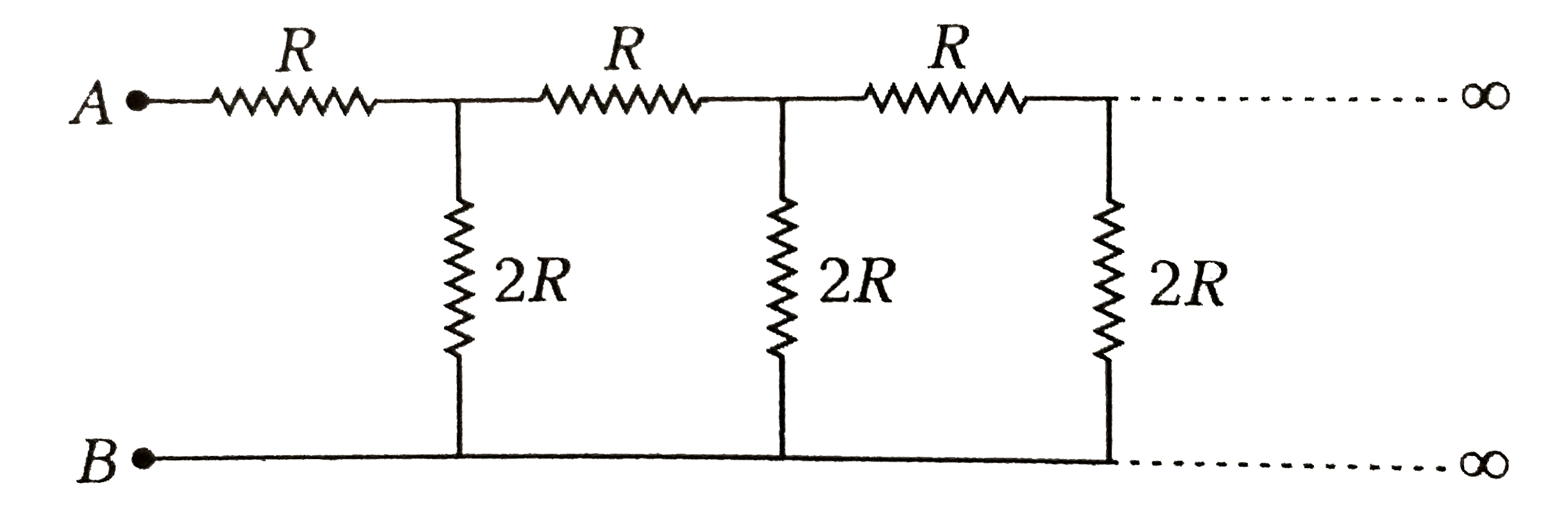 View Solution
View SolutionFind the equivalent Resistance between A and B
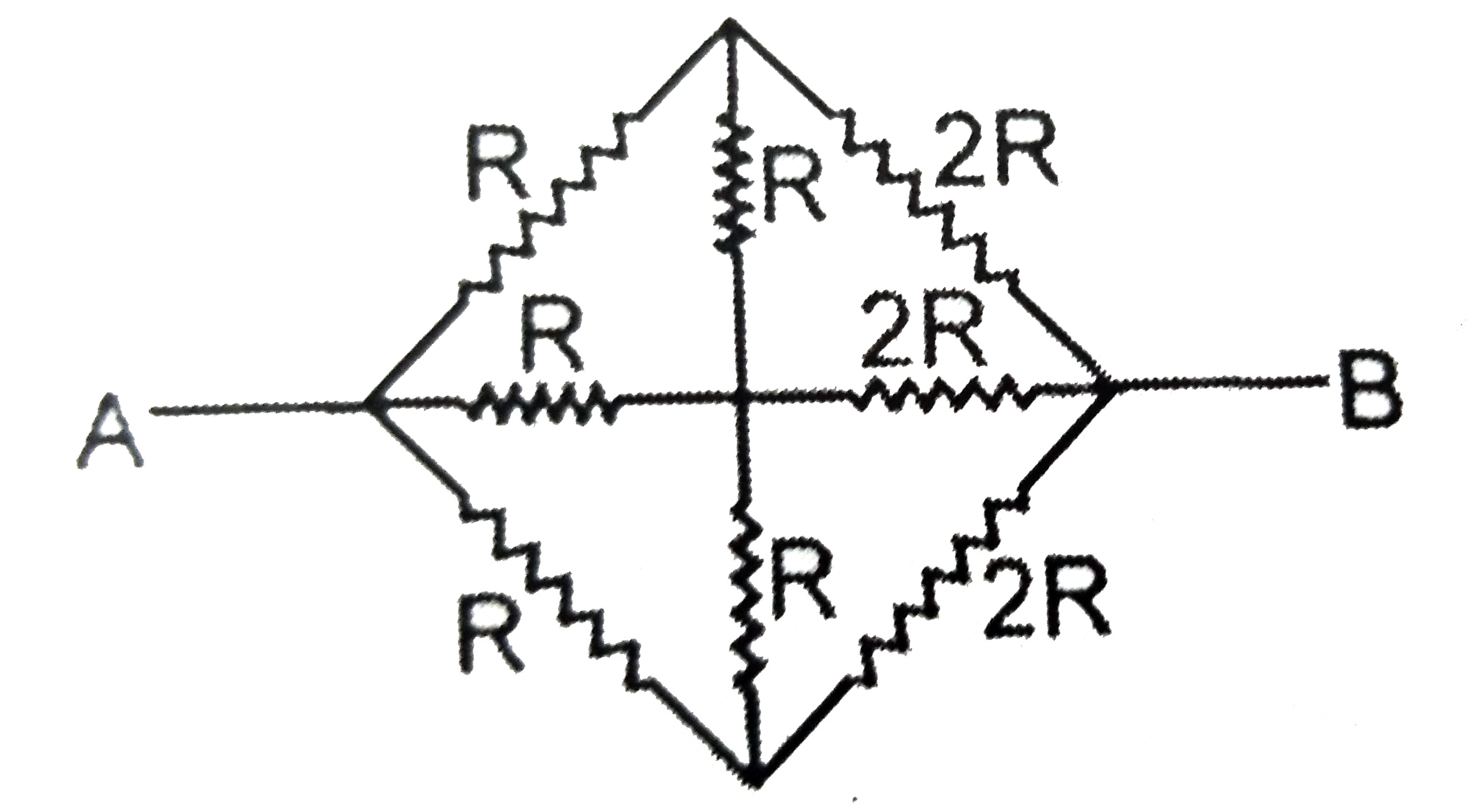 View Solution
View Solution
