Two infinite parallel,non- conducting sheets carry equal positive charge density σ ,One is placed in the yz plane other at distance x=a Take potential V=0 at x=0 then
for 0≤x≤a, potential V=0
for x≥a, potential V=σε0(x−a)
for x≥a, potential V=σε0(x−a)
for x≤0, potential V=σε0x
The correct Answer is:a.,c.,d.
To solve the problem of determining the electric potential due to two infinite parallel non-conducting sheets with equal positive charge density σ, we will analyze the electric field and potential in different regions defined by the positions of the sheets.
Step 1: Understand the Configuration
We have two infinite parallel sheets:
- The first sheet is located in the yz-plane (at x=0).
- The second sheet is at a distance x=a.
Both sheets have a uniform positive charge density σ.
Step 2: Determine the Electric Field
The electric field due to an infinite sheet of charge with charge density σ is given by:
E=σ2ϵ0
This electric field points away from the sheet if the charge is positive.
Regions to consider:
1. Region 1: x<0 (to the left of the first sheet)
2. Region 2: 0<x<a (between the two sheets)
3. Region 3: x>a (to the right of the second sheet)
Electric Field in Each Region:
- For x<0: The electric field due to the first sheet is directed to the left (negative x-direction), and there is no contribution from the second sheet. Thus:
E=−σ2ϵ0
- For 0<x<a: The electric fields from both sheets add up:
E=σ2ϵ0+σ2ϵ0=σϵ0
- For x>a: The electric field due to both sheets is directed to the right:
E=σ2ϵ0+σ2ϵ0=σϵ0
Step 3: Calculate the Potential
The potential difference V between two points is given by:
V=−∫Edx
Potential in Each Region:
1. For x<0:
- Taking V=0 at x=0:
V(x)=V(0)+∫x0−σ2ϵ0dx=0−(−σ2ϵ0⋅x)=σ2ϵ0x
2. For 0<x<a:
- Since the electric field is constant:
V(x)=V(0)+∫x0σϵ0dx=0+σϵ0⋅x=σϵ0x
3. For x>a:
- The potential at x=a is:
V(a)=σϵ0a
- Now, for x>a:
V(x)=V(a)−∫xaσϵ0dx=σϵ0a−σϵ0(x−a)=σϵ0(a−x)
Summary of Potential in Different Regions:
- For x<0: V(x)=σ2ϵ0x
- For 0<x<a: V(x)=σϵ0x
- For x>a: V(x)=σϵ0(a−x)
Final Answer:
- Option 1: For 0<x<a, V=0 is incorrect.
- Option 2: For x>a, V=−σϵ0(x−a) is correct.
- Option 3: Incorrect.
- Option 4: For x<0, V=σ2ϵ0x is correct.
We have two infinite parallel sheets:
- The first sheet is located in the yz-plane (at x=0).
- The second sheet is at a distance x=a.
The electric field due to an infinite sheet of charge with charge density σ is given by:
E=σ2ϵ0
This electric field points away from the sheet if the charge is positive.
1. Region 1: x<0 (to the left of the first sheet)
2. Region 2: 0<x<a (between the two sheets)
3. Region 3: x>a (to the right of the second sheet)
- For x<0: The electric field due to the first sheet is directed to the left (negative x-direction), and there is no contribution from the second sheet. Thus:
E=−σ2ϵ0
- For 0<x<a: The electric fields from both sheets add up:
E=σ2ϵ0+σ2ϵ0=σϵ0
E=σ2ϵ0+σ2ϵ0=σϵ0
The potential difference V between two points is given by:
V=−∫Edx
- Taking V=0 at x=0:
V(x)=V(0)+∫x0−σ2ϵ0dx=0−(−σ2ϵ0⋅x)=σ2ϵ0x
- Since the electric field is constant:
V(x)=V(0)+∫x0σϵ0dx=0+σϵ0⋅x=σϵ0x
- The potential at x=a is:
V(a)=σϵ0a
- Now, for x>a:
V(x)=V(a)−∫xaσϵ0dx=σϵ0a−σϵ0(x−a)=σϵ0(a−x)
- For x<0: V(x)=σ2ϵ0x
- For 0<x<a: V(x)=σϵ0x
- For x>a: V(x)=σϵ0(a−x)
- Option 1: For 0<x<a, V=0 is incorrect.
- Option 2: For x>a, V=−σϵ0(x−a) is correct.
- Option 3: Incorrect.
- Option 4: For x<0, V=σ2ϵ0x is correct.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Integer
5 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Single Correct
56 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Electric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionAn infinite non-conducting plane with uniform charge density σ is kept parallel to yz plane and at a distance 'd' from a dipole →p which itself is located at the origin. An equipotential surface for this system is spherical, centred at origin, having radius R(<d). Given that R=(pnπσ)1/3, find the integer n

View Solution
Knowledge Check
Two infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities σ. Electric field at a point between the sheets is
Aσ2ε0Bσε0CzeroDdepends on the location of the point
In front of a uniformly charged infinite non-conducting sheet of surface charge density σ, a point charge q0 is shifted slowly from a distance a to b(b>a). If work done by external agent is W, then find out relation between the given parameters.
View SolutionAn infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
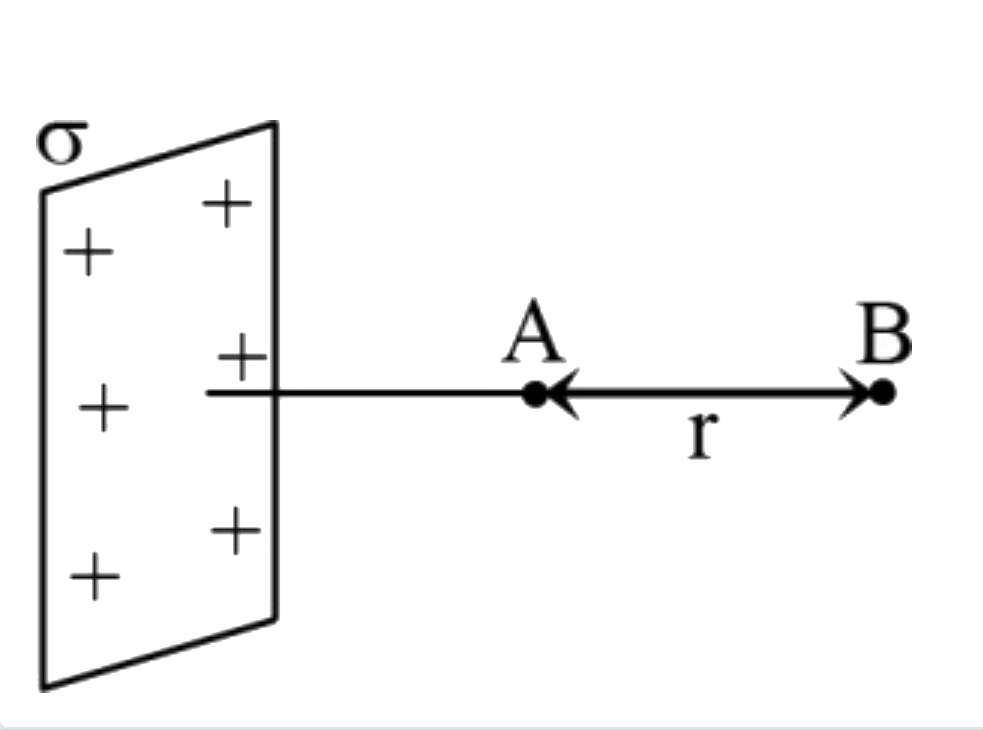
View SolutionTwo infinite, non-conducting sheets of charge are parallel to each other, as shown in figure. The sheet on the left has a uniform surface charge density σ, and the one on the right has a uniform charge density −σ. Calculate the electric field at points (a) to the left of, (b) in between, and (c) to the right of the two sheets.

View SolutionAn infinite sheet of charge has surface charge density σ . The separation between two equipotential surfaces, whose potential differ by V is:
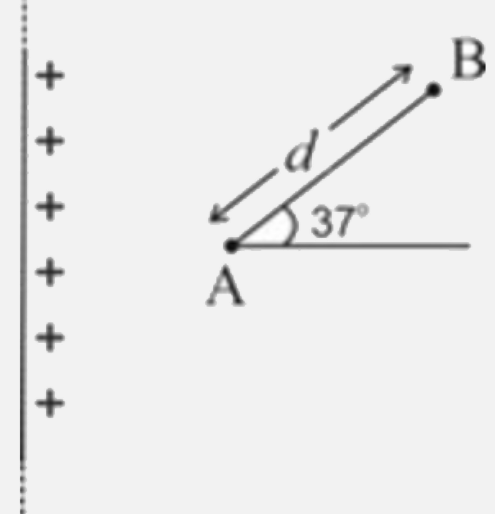
View SolutionAn infinite thin non - conducting sheet has uniform surface charge density σ. Find the potential difference VA−VB between points A and B as shown in the figure. The line AB makes an angle of 37∘ with the normal to the sheet. (sin37∘=35)
View SolutionTwo infinite sheets of unifrom charge density +σand−σ are parallel to each other as shown in the figure. Electric field at the
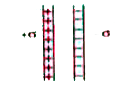
View SolutionTwo large conducting plates are placed parallel to each other nad they carry equal and opposite charges with surface density σ as shown in figure (30-E6). Find the electric field (a) at the left of the plates, (b) in between the plates and © at the right of the plates.

View Solution
