A small conducting sphere of radius a, carrying a charge +Q, is placed inside an equal and oppositely charged conducting shell of radius b such that their centers coincide. Determine the potential at a point which is at a distance c from center such that a<c<b.
k(Q/c+Q/b)
k(Q/a+Q/b)
k(Q/a−Q/b)
k(Q/c−Q/b)
The correct Answer is:d
To determine the potential at a point which is at a distance c from the center of a small conducting sphere of radius a carrying a charge +Q, placed inside an oppositely charged conducting shell of radius b, we can follow these steps:
1. Understanding the Configuration:
- We have a small conducting sphere with charge +Q and radius a.
- Surrounding this sphere is a conducting shell with charge −Q and radius b.
- The centers of both the sphere and the shell coincide.
2. Identifying the Region:
- We need to find the electric potential at a point located at a distance c from the center, where a<c<b.
3. Potential Due to the Inner Sphere:
- The potential Vc at a distance c from the center due to the inner sphere (which has charge +Q) is given by the formula:
Vinner=kQc
- Here, k is Coulomb's constant.
4. Potential Due to the Outer Shell:
- The outer shell has a charge of −Q. The potential inside a conducting shell is constant and equal to the potential at its surface.
- The potential at the surface of the shell (at radius b) due to the charge −Q is:
Vouter=−kQb
- Since we are at a distance c (where c<b), the potential due to the outer shell remains constant and is equal to −kQb.
5. Calculating the Total Potential:
- The total potential V at the point c is the sum of the potentials due to both the inner sphere and the outer shell:
V=Vinner+Vouter=kQc−kQb
- We can factor out kQ:
V=kQ(1c−1b)
Final Result:
The potential at the point which is at a distance c from the center is:
V=kQ(1c−1b)
- We have a small conducting sphere with charge +Q and radius a.
- Surrounding this sphere is a conducting shell with charge −Q and radius b.
- The centers of both the sphere and the shell coincide.
- We need to find the electric potential at a point located at a distance c from the center, where a<c<b.
- The potential Vc at a distance c from the center due to the inner sphere (which has charge +Q) is given by the formula:
Vinner=kQc
- Here, k is Coulomb's constant.
- The outer shell has a charge of −Q. The potential inside a conducting shell is constant and equal to the potential at its surface.
- The potential at the surface of the shell (at radius b) due to the charge −Q is:
Vouter=−kQb
- Since we are at a distance c (where c<b), the potential due to the outer shell remains constant and is equal to −kQb.
- The total potential V at the point c is the sum of the potentials due to both the inner sphere and the outer shell:
V=Vinner+Vouter=kQc−kQb
- We can factor out kQ:
V=kQ(1c−1b)
The potential at the point which is at a distance c from the center is:
V=kQ(1c−1b)
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionA common test to find the genotype of a hybrid is by
View SolutionA conducting sphere A of radius a, with charge Q, is placed concentrically inside a conducting shell B of radius b. B is earthed. C is the common center of AandB. Study the following statements.
(i) The potential at a distance r from C, where
a≤r≤b,is14πε0(qr)
(ii) The potential difference between AandB is
14πε0Q(1r−1B)
(iii) The potential at a distance romC, where
a≤r≤b,is14πε0Q(1r−1B)
Which of the following statements are correct ?
 .
.
View SolutionA point charge +Q is placed at point B at a distance 2R from the center O of an uncharged thin conducting shell of radius R as shown in figure. If VA be the potential at point A, which is at a radial distance of R/2 from the center of the shell, then
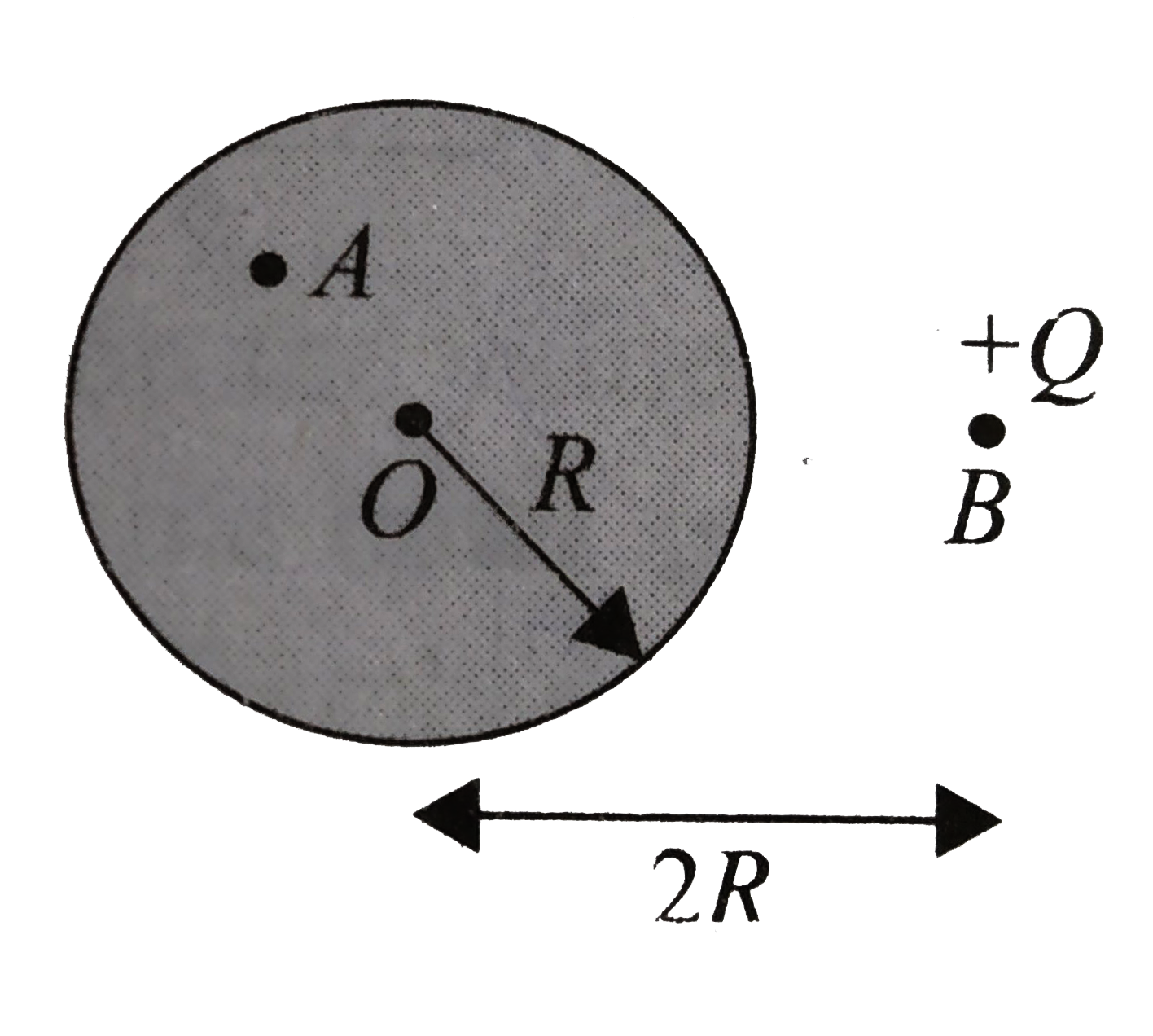
View SolutionInside a charged thin conducting shell of radius R, a point charge +Q is placed as shown in figure potential of shell may be

View SolutionA charge q is placed at a distance of 2R from the centre of a spherical conducting shell of radius R. What is electrical potential, due to charges induced on the shell, at a point which is farthest from the point charge ?
View Solution(a) A charge +Q is placed on a large spherical conducting shell of radius R. Another small conducting sphere of radius r carrying charge 'q' is introduced inside the large shell and is placed at its centre. Find the potential difference between two points, one lying on the sphere and the other on the shell.
(b) How would the charge between the two flow if they are connected by a conducting wire ? Name the device which works on this fact.
View SolutionA charge −Q is unformly distributed over a non-conducting semi-circular rod of radius R. The potential at the center is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View Solution
