Two identical particles are charged and held at a distance of 1m form each pther. They are found to be attraction each other with a force of 0.027N . Now they are connected by a conducting wire so that charge folws between them. Whe the charge flow stop, they are found to be repelling each other with a force of 0.009N. Find the initial charge on each particle.
The correct Answer is:±3μC,±1μC
To solve the problem, we need to determine the initial charges on two identical particles that initially attract each other and then repel after being connected by a conducting wire. We will use Coulomb's law to find the charges.
Step 1: Understand the Initial Conditions
Initially, the two particles attract each other with a force of F1=0.027N. Since they attract, one charge must be positive and the other must be negative. Let’s denote the charges as Q1 and Q2.
Step 2: Apply Coulomb's Law for Attraction
Coulomb's law states that the force between two charges is given by:
F=k|Q1Q2|r2
Here, k=9×109N m2/C2 and r=1m. Since the force is attractive, we can write:
0.027=9×109|Q1Q2|12
This simplifies to:
|Q1Q2|=0.0279×109
Calculating this gives:
|Q1Q2|=3×10−12C2(1)
Step 3: Understand the Conditions After Connecting the Wire
When the particles are connected by a conducting wire, charge flows until both particles have the same charge. Let’s denote the final charge on each particle as Qf. The total charge is conserved, so:
Qf=Q1+Q22
Step 4: Apply Coulomb's Law for Repulsion
After the charge has equalized, the particles repel each other with a force of F2=0.009N. Now both charges are of the same sign (either both positive or both negative), so we can write:
0.009=9×109(Qf)212
This simplifies to:
(Qf)2=0.0099×109
Calculating this gives:
(Qf)2=1×10−12C2(2)
Taking the square root, we find:
Qf=1×10−6C=1μC
Step 5: Relate the Charges
From equation (1), we have:
|Q1Q2|=3×10−12
And from the equalized charge:
Qf=Q1+Q22=1×10−6
Thus,
Q1+Q2=2×10−6(3)
Step 6: Solve the System of Equations
Now we have two equations:
1. Q1+Q2=2×10−6 (from equation 3)
2. Q1Q2=−3×10−12 (from equation 1)
Let Q1=x and Q2=2×10−6−x. Substituting into the second equation gives:
x(2×10−6−x)=−3×10−12
Expanding this:
2×10−6x−x2=−3×10−12
Rearranging gives:
x2−2×10−6x−3×10−12=0
Step 7: Solve the Quadratic Equation
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1, b=−2×10−6, and c=−3×10−12.
Calculating the discriminant:
b2−4ac=(2×10−6)2−4(1)(−3×10−12)=4×10−12+12×10−12=16×10−12
Now substituting back into the formula:
x=2×10−6±√16×10−122
x=2×10−6±4×10−62
This gives two solutions:
1. x=3×10−6C (which is not possible since it exceeds the total charge)
2. x=−1×10−6C
Thus, the charges are:
- Q1=3×10−6C
- Q2=−1×10−6C
Final Answer
The initial charges on the particles are:
- Q1=3μC
- Q2=−1μC
Initially, the two particles attract each other with a force of F1=0.027N. Since they attract, one charge must be positive and the other must be negative. Let’s denote the charges as Q1 and Q2.
Coulomb's law states that the force between two charges is given by:
When the particles are connected by a conducting wire, charge flows until both particles have the same charge. Let’s denote the final charge on each particle as Qf. The total charge is conserved, so:
After the charge has equalized, the particles repel each other with a force of F2=0.009N. Now both charges are of the same sign (either both positive or both negative), so we can write:
From equation (1), we have:
Now we have two equations:
1. Q1+Q2=2×10−6 (from equation 3)
2. Q1Q2=−3×10−12 (from equation 1)
Using the quadratic formula x=−b±√b2−4ac2a:
x=2×10−6±4×10−62
2. x=−1×10−6C
- Q2=−1×10−6C
The initial charges on the particles are:
- Q1=3μC
- Q2=−1μC
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct
47 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Two positive charges separated by a distance 2m repel each other with a force of 0.36N. If the combined charge is 26μC, the charges are
View SolutionTwo identical conducting spheres, fixed in space, attract each other with an electrostatic force of 0.108N when separated by 50.0cm, centre-to-centre. A thin conducting wire then connects the spheres. When the wire is removed, the spheres repel each other with an electrostatic force of 0.0360N. What were the initial charges on the spheres?
View Solution
Knowledge Check
Two point charges of +3μCand+4μC repel each other with a force of 10 N. If each is given an additional charge of −6μC, the new force is
A2 NB4 NC5 ND7.5 N
The centres of two identical small conducting spheres are 1m apart. They carry charge of opposite kind and attract each other with a force F. When they are connected by a conducting thin wire they repel each other with a force F/3. What is the ratio of magnitude of charge carried by the sphere initially ?
View SolutionTwo point charges +10 muC and +20 muC repel each other with a force of 100N. If a charge of-2 muC is added to each charge, then force between them will become
View SolutionTwo identical metals balls with charges +2Q and −Q are separated by some distance and exert a force F on each other . They are joined by a conducting wire , which is then removed. The force between them will now be
View SolutionTwo charges spheres are separated at a distance d exert a force F on each other, if charges are doubled and distance between them is doubled then the force is
View SolutionTwo point charges repel each other with a force of 100N. One of the charges is increased by 10% and the other is reduced by 10% . The new force of repulsion at the same distance would be
View SolutionThe two conducting spherical shells are joined by a conducting wire and cut after some time when charge stops flowing. Find out the charge on each sphere after that.
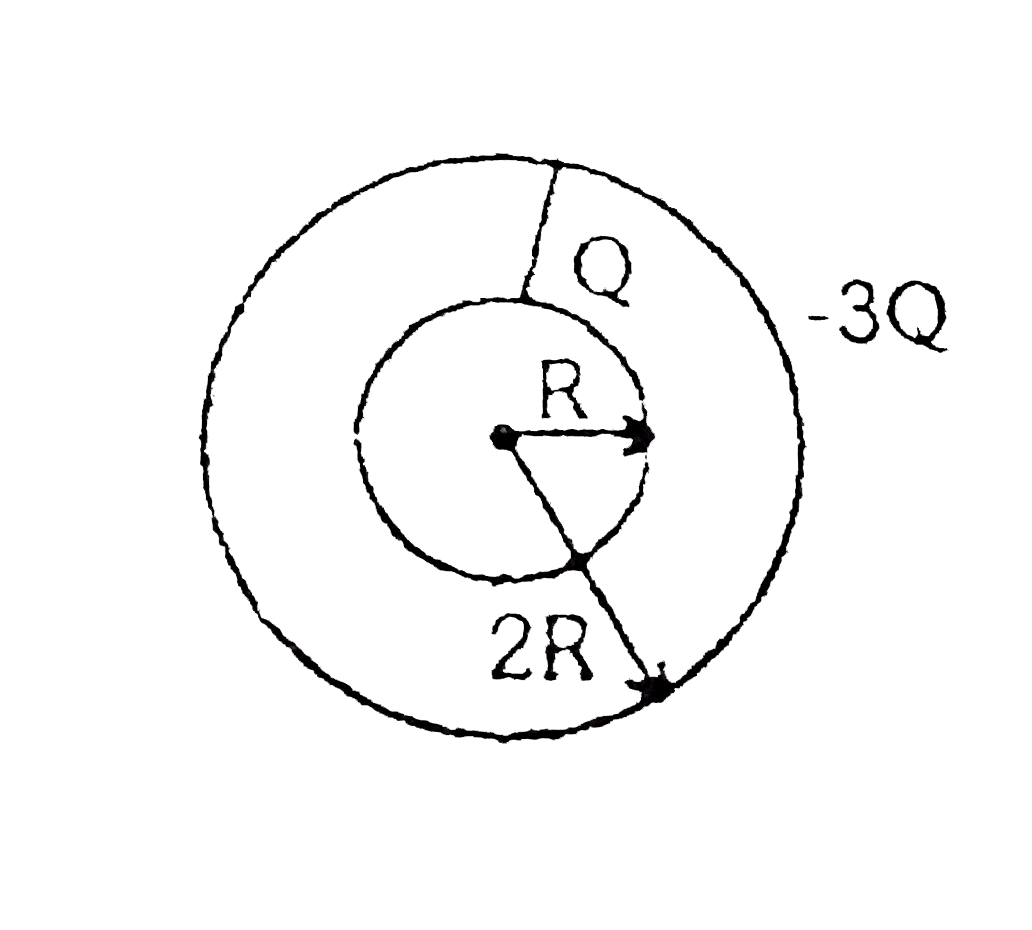
View SolutionTwo ball with charges 5μCand10μC are at a distance of 1 m from each other. In order to reduce the distance between them to 0.5 m , the amount of work to be performed is
View Solution
