An electric field is defined in terms of q0 a small positive charge. If the definition was in terms of a small negative charge of the same magnitude, then compared to the original field the newly defined electric field.
(a) would point in the same direction and have the same magnitude.
(b) would point in the opposite direction and have the same magnitude.
(c ) would point in the same direction and have the different magnitude.
(d) would point in the opposite direction and have the different magnitude.
To solve the problem, we need to analyze how the definition of the electric field changes when we switch from a positive charge q0 to a negative charge of the same magnitude.
1. Understanding Electric Field Definition:
The electric field →E at a point in space due to a charge Q is defined as the force →F experienced by a small positive test charge q0 placed at that point, divided by the magnitude of that charge:
→E=→Fq0
2. Magnitude of Electric Field:
When we define the electric field using a small negative charge −q0 of the same magnitude, the force →F acting on this negative charge due to the source charge Q remains the same in magnitude but will act in the opposite direction (since opposite charges attract). Thus, the magnitude of the electric field remains unchanged:
|→E|=|→F||q0|=|→F||−q0|
Therefore, the magnitude of the electric field is the same.
3. Direction of Electric Field:
When we substitute −q0 into the equation, the electric field can be expressed as:
→Enew=→F−q0
Since →F is directed towards the source charge (for a negative test charge), the direction of →Enew will be opposite to that of →E defined with the positive charge.
4. Conclusion:
- The magnitude of the electric field remains the same.
- The direction of the electric field reverses when using a negative charge.
Thus, the correct answer is:
(b) would point in the opposite direction and have the same magnitude.
The electric field →E at a point in space due to a charge Q is defined as the force →F experienced by a small positive test charge q0 placed at that point, divided by the magnitude of that charge:
→E=→Fq0
When we define the electric field using a small negative charge −q0 of the same magnitude, the force →F acting on this negative charge due to the source charge Q remains the same in magnitude but will act in the opposite direction (since opposite charges attract). Thus, the magnitude of the electric field remains unchanged:
|→E|=|→F||q0|=|→F||−q0|
Therefore, the magnitude of the electric field is the same.
When we substitute −q0 into the equation, the electric field can be expressed as:
→Enew=→F−q0
Since →F is directed towards the source charge (for a negative test charge), the direction of →Enew will be opposite to that of →E defined with the positive charge.
- The magnitude of the electric field remains the same.
- The direction of the electric field reverses when using a negative charge.
(b) would point in the opposite direction and have the same magnitude.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples
10 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Figure shows the field lines of a point negative charge. In going from B to A, the kinetic energy of a small negative charge will

View SolutionTwo parallel wires are carrying electric currents of equal magnitude and in the same direction. They
View SolutionA negative charge is moved by an external agent in the direction of electric field. Then
 .
.
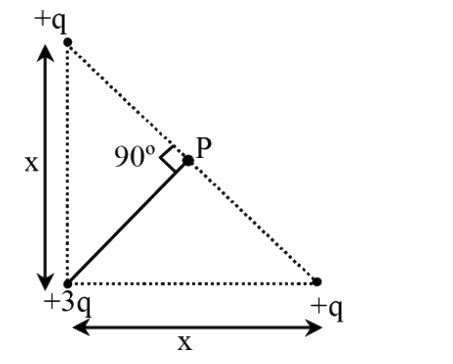
View SolutionThe magnitude and direction of the electric field at point P can be best represented by
View SolutionA uniform electric field and a uniform magneitc field exist in a region in the same direction An electron is projected with velocity pointed in the same direction the electron will
View SolutionA Point charge produces an electric field in room. What is its direction?
View SolutionFind the magnitude and direction of magnetic field at point O in the following case

View SolutionA positive point charge q is placed at a distance 2 R from the surface of a metallic shell of radius R. the electric field at centre of shell due to indouced charge has magnitude

View SolutionFind the magnitude of the electric field at a point 4 cm away from a line charge of density 2×10−6Cm−1.
View SolutionA positive charge and a negative charge are initially at rest. If same electric field is applied on them.
View Solution
